流体力学

一.流体的性质与静力学

1.帕斯卡原理

施加于静止流体上一点的压强将以等值同时传递到各点。

2.液体压强公式

P = ρgh

二.流动的基础方程式

1.流体力学中使用的各种专业术语

1.1定常流和非定常流

流动速度不随时间变化而变化的流动称为定常流，否则就是非定常流

1.2均匀流与非均匀流

建立一个X-Y的直角坐标系，如果只有X轴方向的速度U，那么叫做均匀流；如果既有X轴方向的速度分量，又有Y轴方向的速度分量，那么叫做非均匀流。 举例：

一个笔直的水管里流动的水是均匀流，在一条小溪里面插入一根木棒，木棒周围的水就是非均匀流。

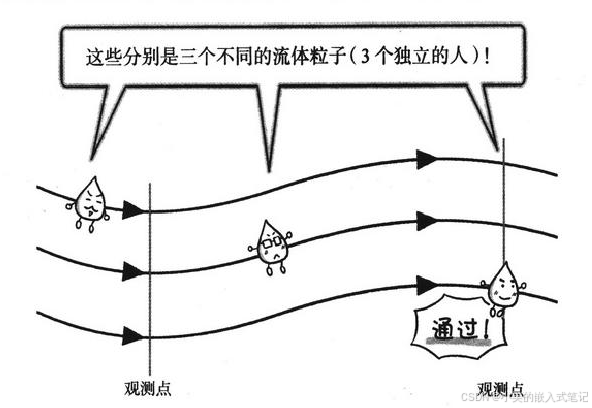
1.3拉格朗日法与欧拉法

拉格朗日法：一直跟踪观察同一个流体粒子的方法

欧拉法：持续观测特定的位置，并测量通过其中的流体粒子的方法。

1.4流线、迹线和流管

流线：将流体中几个不同位置粒子流速矢量用线连起来，画成曲线

迹线：将同一个粒子，不同时间处在的位置用线连起来，形成的轨迹就是迹线

流管：假想将刚才的流线按照一定的数量集结成管，这种假想的管道就叫流管

2.连续性方程

2.1 流体的质量守恒定理

• 定义 ：在流体力学中，质量守恒定理表明，在一个封闭系统中，无论发生何种物理过程，系统内流体的总质量始终保持不变。也就是说，在没有物质流入或流出系统的情况下，系统内流体质量不会凭空增加或减少。
• 物理意义 ：它体现了自然界中物质的基本属性，即物质既不能被创造也不能被消灭，只能从一种形式转化为另一种形式或从一个位置转移到另一个位置。对于流体而言，在任何流动过程中，流体的质量在整个流动区域内是守恒的。

2.2连续性方程

2.3应用

液体以速度V1从一个大直径管道（管道直径A1），流入一个较小直径的管道（管道直径A2），计算这个时候液体的流速V2。

我们根据连续性方程ρV1A1=ρV2A2就可以计算出V2的值。

其实连续性方程就是告诉我们单位时间内流入一个封闭系统的流量=流入这个封闭系统的流量。

3.伯努利定理（流体的能量守恒定理）

3.1 流体能量公式

流体能量=动能+势能+压力能

E（J）= ½mu²+mgh+pV(u为速度，p为压强，V为体积)

由于流体的形状不固定，用质量来描述液体比较困难，同时由于密度ρ的物理含义就是单位体积的质量，所以上述公式就变为

3.2 伯努利定理

这个定理成立的条件是沿着流线方向。当流体为理想流体时，能量恒定为常数。

同时说明下为什么压强这个力学单位会和能量联系起来：

根据上式，压强的物理含义可以理解为单位体积的能量。

3.3伯努利定理的应用举例

一根橡胶水管，中间有一段直径变小，这个直径变小的地方的压强是怎样变化的？

由于管子是水平的，我们根据伯努利定理，流经细管的流体动能+压力能大小不变，而根据连续性方程，流经细管的流量不会变化，

那么流速就会增加，动能也就会增加，那么相对的，压强就会减小。

4.动量守恒定理

4.1 物体的动量守恒定理

我们举一个简单的例子，将小球做钟摆运动，起始速度为U1，手用F的力阻止小球向下摆动△t秒：

此时的动量守恒关系式为：

其中F△t是冲量

也就是变化后的动量-变化前的动量=冲量。

4.2流体的能量守恒定理

（1）观察领域

由于流体不像固体一样有个固定的形状，相对来说不好观察，所以引入观察领域的概念。通过计算流入流出观察领域单位时间内的动量变化，

就能知道观察领域对流体施加的力。

上图是一个变径管道，红色框部分就是观察领域，变径部分对流体产生F的力。

mU2-mU1=F△t，m=ρV，Q（流量）=V/△t

综上ρQU2-ρQU1 = F,由此可见检查领域内单位时间内动量变= 管道收缩部分对流体施加的力的作用。

那么这个定理有什么用呢？举例来说，当水库经过大坝以后，直径变小了，这个时候大坝就是个检查领域，我们通过

水流单位时间内的动量变化量，就知道了施加在大坝上的压力。

三.层流和湍流

1.1黏性和黏性力

黏性：表示流体黏黏糊糊的程度

黏性力：有黏性的物体会产生黏性力，黏性力会阻碍流体的流动

1.2 理想流体与黏性流体

上图是管道中理想流体和黏性流体的速度分布图。黏性流体越靠近管道内壁速度越慢。需要注意的是，之前所说的伯努利定理

和动能守恒定理都是 针对理想流体来说的。

1.3 速度梯度

上图是水流过竹制流水槽的直角坐标系图，Y轴为距离竹子的距离，X为水的流速。du/dy就是速度的梯度，速度梯度的含义

就是位置移动dy,速度变化的量du。有图上可以看出从竹壁到中心，速度梯度是越來越小的，也就是說越靠近竹壁，速度变慢

得越快。也就是说黏性变强了。

1.4 黏性应力

黏性应力=τ，单位Pa

（1）黏性牛顿定理：

μ是粘度，单位Pa.S

（2）运动黏度：

2.雷诺数与层流湍流

雷诺数表示的是惯性力与黏性力的比值，公式为：

我们以用吸管吸奶昔来解释这个式子：

物理意义

• 反映流动状态 ：雷诺数较小时，黏性力对流体的作用占主导地位，流体流动比较平稳，呈现层流状态，流体质点沿着平行于管道轴线或物体表面的方向做有规则的分层流动，各层之间互不混合。当雷诺数较大时，惯性力的作用相对增强，流体流动变得不稳定，会出现湍流状态，流体质点在流动过程中会发生强烈的混合和随机的脉动。

雷诺数Re=2320是层流和湍流的分界线，这个值被称为临界雷诺数，大于这个值就是湍流。

层流是指流体在流动过程中，流体质点沿着与流动方向平行的方向作平滑直线运动，各层流体之间互不混合，呈现出分层流动的状态，就像一层一层的流体在相互平行地滑动。

湍流是指流体在流动时，流体质点除了有沿着流动方向的总体运动外，还存在着强烈的无规则脉动和混合，流体质点的运动轨迹极其复杂且不规则，流体的速度、压力等物理量在时间和空间上都呈现出随机变化的特性。

3.管道内的层流

三个重要概念：流速、流量、能量

(1)流速

对于吸管里的液体，无论是理想流体和黏性流体，根据连续方程，吸管内每个横截面的平均流量是一样的。

对于上图所示的吸管，吸管内同一截面上不同点的流体速度是不同的，具体公式如下：

u:表示速度，μ:表示黏度，dp/dx:表示压力梯度，即沿着前进方向每改变微小的距离，压力改变的程度。也就是说速度以管道中心

为最大值，向两边呈现一个抛物线，这种呈抛物线形式分布的流动称为“泊肃叶流”。

（2）流量

还是以吸饮料为例，下流图代表嘴巴，上流处代表饮料。流入嘴里饮料的流量公式为：

（3）能量

当我们用吸管吸饮料的时候，由于液体有黏度，运动时有阻力，所以会产生能量损耗，这个损耗我们叫做摩擦损失，如下图所示

摩擦损失的计算公式“达西-魏斯巴赫公式”为：

λ为管道摩擦系数，在层流情况下λ=64/RE

由于这个摩擦损失，所以之前提到的伯努利方程不在适用，这个时候 就用到管流 伯努利方程：

,E(S)是随着S的函数。

（4）.补充：软管的压强损失

下面我们分几种情况说明损失系数的大小：

1.急剧扩大管道的情况

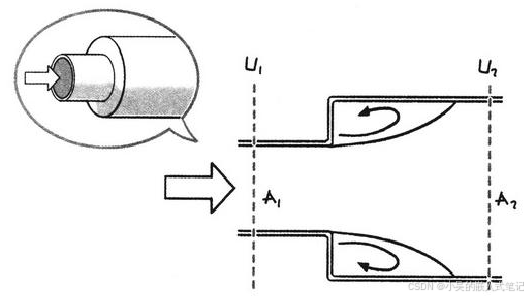
2.急剧缩小管道的情况

3.管道弯曲的情况

四.阻力与升力

1.升力和阻力的定义

升力 ：是指流体作用在物体上，与物体运动方向垂直的力，它能使物体在垂直方向上产生上升或有上升的趋势

阻力 ：是指流体作用在物体上，与物体运动方向相反的力，它会阻碍物体在流体中的运动

2.流线曲率定理

以上图机翼为例，△P/△r表示半径r方向上的压强变化。

3.阻力和升力公式

阻力公式：

是阻力系数，ρ是流体密度，v是速度，S是面对阻力方向的投影面积

升力公式：

CL是升力系数，ρ是流体密度，v是速度，S是升力方向的投影面积

4.迎角与分离

（1）迎角与升力系数以及阻力系数的关系图

如图中所示，当迎角过大时，升力系数会降低。

以飞机为例，当机翼迎角太大的时候，风不能进入机翼周围，在机翼上发生风的分离现象，就是气流分离现象。然后机翼后方会形成涡旋，示意图如下：

5.作用与旋转物体的力（马格努斯效应）

1.投出的高速旋转的球为什么会拐弯

假设有一个棒球由投球手投出，飞向接球手，球的旋转方向为逆时针，此时球和周围的气流情况如下所示：

由于球旋转会带动附近的气流，所以左侧气流的速度<右侧气流的速度，根据伯努利定理

球的左侧速度小于右侧，所以左侧压强大，此时球向右偏转。

6.流动分离（高尔夫球表面为什么做成坑坑洼洼的）

如上图所示，当高尔夫球表面 坑坑洼洼的时候，这些坑洼里面就会产生小涡旋,也就是形成湍流。那么我们为什么要把层流改为湍流呢？

原因是高尔夫球飞行的时候，会产生流体分离。

如上图所示，高尔夫球表面有一个边界层，厚度很薄（大约只有1mm）。流体在边界层的内外侧流动性质差别很大，在边界层内侧，速度梯度很大，流体因为黏性力速度降低得很快，而在分界层外侧，流体速度几乎受到的影响较小。越靠近球体表面，黏性力越大，流体越难流动，当迎角大于一定值时就会发生流体分离（飞机机翼那里有说明），在下流出就会形成分离涡流。

如上图所示，湍流相对于层流来说，分离角度更大，形成的分离旋涡较小。

而形成的分离涡流压强较小，就相当于会形成阻力。所以在高尔夫球表面，湍流产生的阻力就小于层流。