相关性分析
分析两个特征的相关程度叫做相关性分析，比如“身高”与“体重”两个特征，就可以使用相关性分析找到两者的相关关系。
正相关/负相关/不相关
图表
分析两组数量不大的数据时，可以用图表法，常见的图表法有以下两种：
- 折线（时间维度）：双坐标折线图
- 散点图
图表可以清晰的展现相关关系，但无法准确度量，且缺乏说服力。
协方差
协方差公公式如下：
x和y分别表示的是两个特征，这两个特征都有n条：
原理如下：
当协方差>0表示两个特征正相关，协方差<0表示两个特征负相关。
不能通过协方差判断两个特征相关性强弱。
协方差值小可能是由两个原因引起的：
- 方差小，即数据不离散。
- 相关性弱。
协方差矩阵
协方差矩阵反映的是两两的相关性，其每个元素是各个特征之间的协方差。
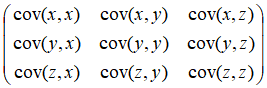
协方差矩阵# 相关性分析
分析两个特征的相关程度叫做相关性分析，比如“身高”与“体重”两个特征，就可以使用相关性分析找到两者的相关关系。## 正相关/负相关/不相关### 图表分析两组数量不大的数据时，可以用图表法，常见的图表法有以下两种：1. 折线（时间维度）：双坐标折线图2. 散点图图表可以清晰的展现相关关系，但无法准确度量，且缺乏说服力。### 协方差协方差公公式如下：x和y分别表示的是两个特征，这两个特征都有n条：原理如下：当协方差>0表示两个特征正相关，协方差<0表示两个特征负相关。>不能通过协方差判断两个特征相关性强弱。>协方差值小可能是由两个原因引起的：>1. 方差小，即数据不理三>2. 相关性弱。### 协方差矩阵协方差矩阵反映的是两两的相关性，其每个元素是各个特征之间的协方差。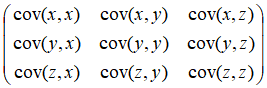
- 对角线元素决定了图形是圆还是扁。
- 非对角线元素决定了分布图形的轴向（扁的方向）。
相关性强弱
相关系数
那么为了判断相关性强弱，可以排除协方差中相关性的影响，这就是皮尔逊相关系数，即：
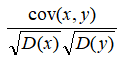
建模
一元回归及多元回归
一元回归
如果两个特征线性相关，那么可以对这两个特征线性拟合。
多元回归
多元回归首先要确定变量个数，并确定自/因变量，接下来就可以具体问题具体分析。
显著性检验
可以通过显著性检验证明两个变量x，y之间是否具有显著的线性关系。
F检验
通过F检验对一元线性回归效果进行分析。
一元线性回归的数学模型：
原理： 若y=a+bx+ε中的b=0，说明x的变化对y没有影响，这时回归方程
y
^
=
a
^
+
b
^
x
\hat{y}=\hat{a}+\hat{b}x
y^=a^+b^x就不能近似的描述y和x的关系，因此为了判断x与y再见是否存在线性关系，只需检验假设
H
0
：
b
=
0
H_0：b=0
H0：b=0，接受原假设，表示不能认为x，y再见存在线性相关关系。
构造统计量：
- 变量y的离差平方和（类似于方差）：
L
y
y
=
∑
i
=
1
n
(
y
i
−
y
‾
)
=
∑
i
=
1
n
(
y
i
−
y
i
^
)
+
∑
i
=
1
n
(
y
i
^
−
y
‾
)
=
Q
+
U
L_{yy}=\sum_{i=1}^n(y_i-\overline{y})=\sum_{i=1}^n(y_i-\hat{y_i})+\sum_{i=1}^n(\hat{y_i}-\overline{y})=Q+U
Lyy=i=1∑n(yi−y)=i=1∑n(yi−yi^)+i=1∑n(yi^−y)=Q+U
其中， Q = ∑ i = 1 n ( y i − y i ^ ) 2 Q=\sum_{i=1}^n(y_i-\hat{y_i})^2 Q=∑i=1n(yi−yi^)2表示真实值和预测值之间的离差平方和，它表示除x对y的线性影响之外一切可能引起y值变化的因素，也称为误差平方和或残差平方和。 U = ∑ i = 1 n ( y i ^ − y ‾ ) 2 U=\sum_{i=1}^n(\hat{y_i}-\overline{y})^2 U=∑i=1n(yi^−y)2表示预测值和平均值 y ‾ \overline{y} y的离差平方和，由于 y i ^ = a ^ + b ^ x i \hat{y_i}=\hat{a}+\hat{b}x_i yi^=a^+b^xi，可以把 y i ^ − y ‾ \hat{y_i}-\overline{y} yi^−y看成是由x的变化引起的y值的变化，称之为回归平方和。
而： U = ∑ i = 1 n ( y i ^ − y ‾ ) = b 2 ^ ∑ i = 1 n ( x i − x ‾ ) 2 = b 2 ^ L x x = b ^ L x y U=\sum_{i=1}^n(\hat{y_i}-\overline{y})=\hat{b^2}\sum_{i=1}^n(x_i-\overline{x})^2=\hat{b^2}L_{xx}=\hat{b}L_{xy} U=∑i=1n(yi^−y)=b2^∑i=1n(xi−x)2=b2^Lxx=b^Lxy
当 H 0 H_0 H0为真时，统计量：
对于给定的显著性水平 α \alpha α，查自由度为(1,n-2)的F分布临界值表，可得临界值 F α ( 1 , n − 2 ) F_\alpha(1,n-2) Fα(1,n−2)使得 P ( F > F α ( 1 , n − 2 ) ) = α P(F>F_\alpha(1,n-2))=\alpha P(F>Fα(1,n−2))=α，其拒绝域为 W = F > F α ( 1 , n − 2 ) W={F>F_\alpha(1,n-2)} W=F>Fα(1,n−2)
t检验
为了检验假设：
H
0
:
b
=
0
；
H
1
:
b
≠
0
H_0:b=0；H_1:b≠0
H0:b=0；H1:b=0
y
^
=
b
^
x
+
a
^
\hat{y}=\hat{b}x+\hat{a}
y^=b^x+a^，其中，
b
^
=
L
x
y
L
x
x
，
a
^
=
y
‾
−
b
^
x
‾
\hat{b}=\frac{L_{xy}}{L_{xx}}，\hat{a}=\overline{y}-\hat{b}\overline{x}
b^=LxxLxy，a^=y−b^x
L x x = ∑ i = 1 n ( x i − x ‾ ) 2 = ∑ i = 1 n x i 2 − n x ‾ 2 {L_{xx}}=\sum_{i=1}^n(x_i-\overline{x})^2=\sum_{i=1}^n{x_i}^2-n\overline{x}^2 Lxx=∑i=1n(xi−x)2=∑i=1nxi2−nx2
L x y = ∑ i = 1 n ( x i − x ‾ ) ( y i − y ‾ ) = ∑ i = 1 n x i y i − n x ‾ y ‾ {L_{xy}}=\sum_{i=1}^n(x_i-\overline{x})(y_i-\overline{y})=\sum_{i=1}^nx_iy_i-n\overline{x}\overline{y} Lxy=∑i=1n(xi−x)(yi−y)=∑i=1nxiyi−nxy
L y y = ∑ i = 1 n ( y i − y ‾ ) 2 = ∑ i = 1 n y i 2 − n y ‾ 2 {L_{yy}}=\sum_{i=1}^n(y_i-\overline{y})^2=\sum_{i=1}^n{y_i}^2-n\overline{y}^2 Lyy=∑i=1n(yi−y)2=∑i=1nyi2−ny2
令 r = L x y L x x L y y r=\frac{L_{xy}}{\sqrt{L_{xx}L_{yy}}} r=LxxLyyLxy，此统计量称为积差相关系数。
U = ∑ i = 1 n ( y i ^ − y ‾ ) 2 = b ^ L x y U=\sum_{i=1}^n(\hat{y_i}-\overline{y})^2 = \hat{b}L_{xy} U=∑i=1n(yi^−y)2=b^Lxy
Q
=
L
y
y
−
U
=
L
y
y
−
b
^
L
x
y
=
L
y
y
(
1
−
r
2
)
Q=L_{yy}-U=L_{yy}-\hat{b}L_{xy}=L_{yy}(1-r^2)
Q=Lyy−U=Lyy−b^Lxy=Lyy(1−r2)
不难看出，由于
Q
≥
0
，
L
y
y
≥
0
Q\geq0，L_{yy}\geq0
Q≥0，Lyy≥0，故
(
1
−
r
2
)
≥
0
(1-r^2)\geq0
(1−r2)≥0，即
0
≤
∣
r
∣
≤
1
0\leq|r|\leq1
0≤∣r∣≤1。
|r|越接近1，回归方程对样本数据的拟合程度越好，反之，|r|越接近0，Q越大，回归方程对样本数据拟合程度越差。
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
