Separable case
1. 定义:
2. 用来计算weight的Structured Perceptron演算法:
- 如果我们能找到一个满足上图的feature function,那么我们就可以用Structured Perceptron演算法找到我们所要的weight(这些在深度学习笔记——理论与推导之Structured Learning【Structured Linear Model】(六)中都可以找到)。
- 那么面对很多个y,是否可以顺利在有限次内找到weight呢?答案是可以的,况且只需要(R/δ)^2次,R是同一个x下Φ(x,y)和Φ(x,y’)的最大距离;δ是margin(即第一个图上画的那块)。与y的个数没有关系。
- 证明如下:
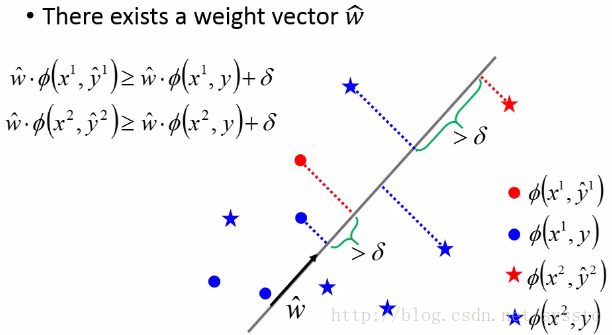
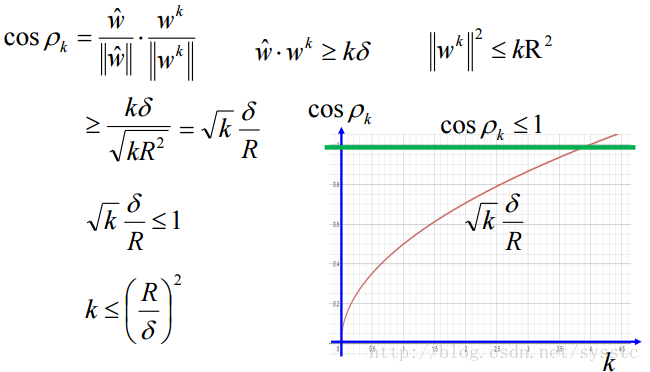
这里的w head 为什么可以不失一般性的假设其长度为1呢,因为我们可以找到w head 可以让data是separable的,那么我们这时候对w head做normalize,这些data也依旧是separable的。 - 当k越大的时候,wk与w head 之间的夹角是越来越小的,也就是cosρk会越来越大:
下面,wk-1要更新的原因就是它乘以Φ(x,y)最大值而找出来的y不是准确的y,因此,下图后面这项是小于0的。接下来假设两个feature之间的距离的最大值是R。因此有了以下的推导:
所以我们现在得到两个结论:
因此我们可以发现w的迭代次数是有穷的,且与y无关。
- 证明如下:
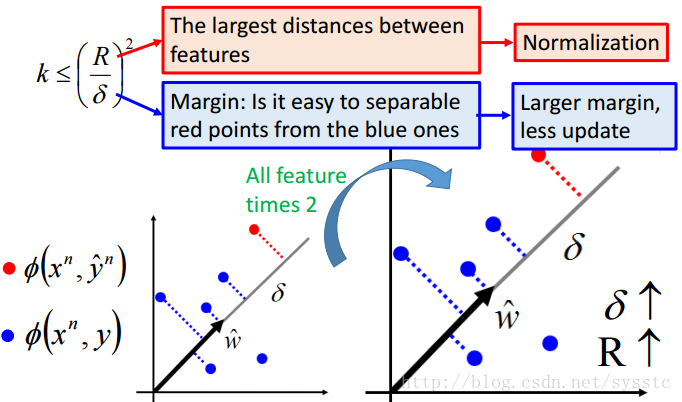
- 那么如何让训练速度更快呢?
要真正改变点才能让训练速度变快,如果只是单方面的放大图片,那么由于R变大了,δ也会变大,这是没有用的,如下图:
Non-separable case
1. 定义:
如果今天我们没有vector可以让正确和错误答案分开(无法让正确答案的F(x,y)高出其他错误答案),而在这些weights vector还是可以辨别出好坏:
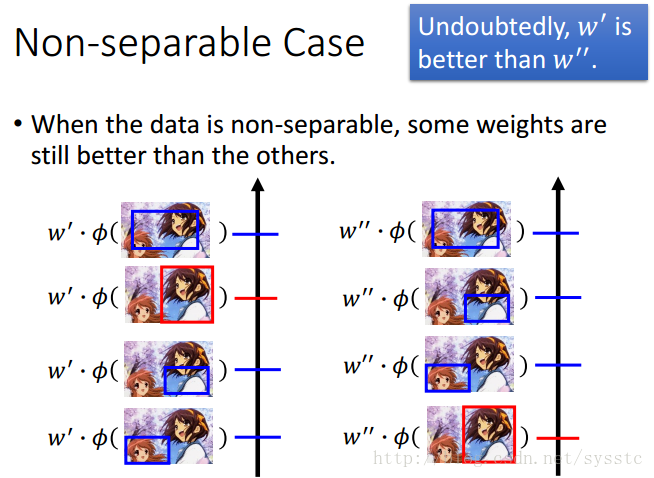
因此在这些情况下,我们还是可以定义一些Evaluation 去判断weight的好坏。
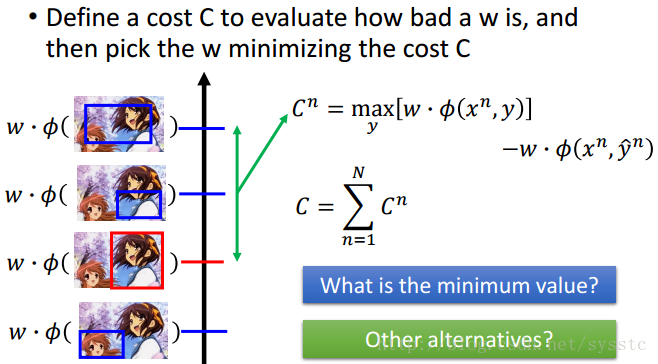
2. Cost Function
接下来,我们定义一个cost function来判断weight有多不好。下面就是用第一名的y的value减去正确的y的value。那我们接下来考虑两个问题:a) 这个值最小是多少,答案:一定大于0,因为如果w*Φ(xn,y head n)是最大值,那么Cn就变成了0。b) 还有没有其他的选择呢?
3. 梯度下降算法(Gradient Descent)
接下来我们需要的是计算Cost function的(Stochastic)Gradient Descent:
- 我们可以对每一个由w分割开的region进行微分。
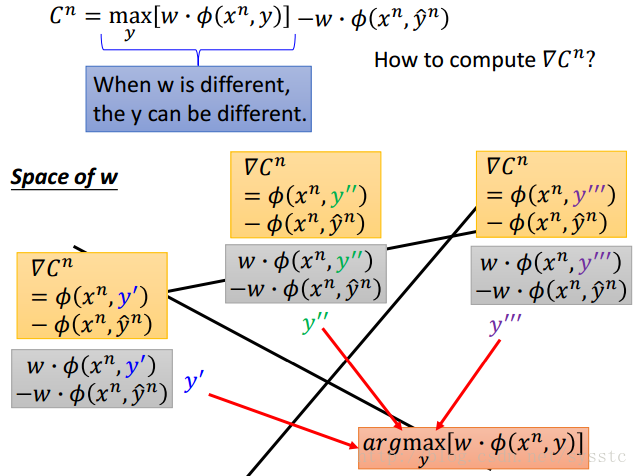
下面是过程(η是Learning rate):
Considering Errors
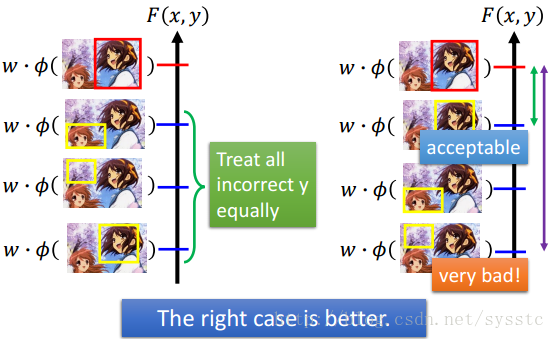
1. 问题引入:
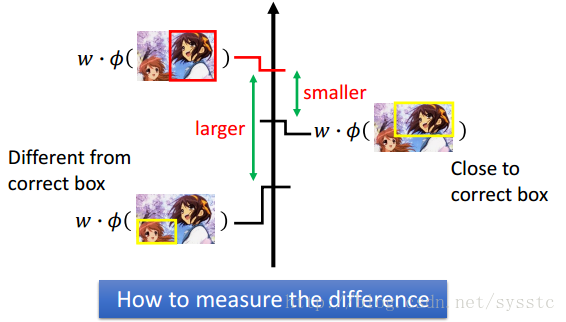
现在我们需要考虑一个问题,就是我们对待错误都是同等的在看。可是有的明明误差大很多,如下:
2. 思路:
那么我们应该如何定义准确值和错误值之间的差距呢?
3. 解决方法:Error Function与更新后的Cost Function
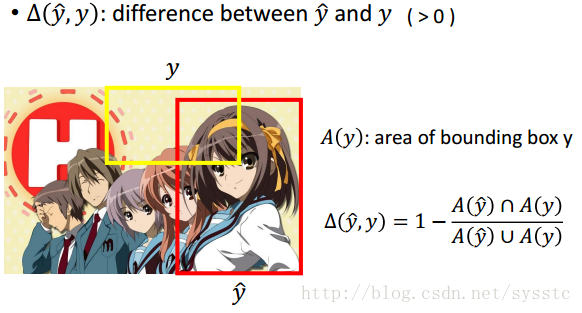
- Error Function:定义正确值和错误值之间的差距。
- Another Cost Function:将Error Function带入到之前的Cost Function中:
- Gradient Descent:
参考之前没做Error Function时的Gradient Descent:
这里与没做Error Function的时候不同的一点,也就是最后算出来的y值不同,所以:
- Another Viewpoint:
- 因为最小化新的成本函数就是在最小化错误的上界,即:
因为C’很难计算,我们不知道它会不会是一个阶梯状的函数,所以,我们现在通过来最小化它。
- 那么为什么
呢,即:
- 因为最小化新的成本函数就是在最小化错误的上界,即:
- More Cost Functions:
Regularization
- 我们知道w越接近0就越能减小mismatch带来的影响,所以我们这里在原本的C的基础上进行修改,添加了一个1/2*||w||^2这项,令w趋于0,就可以减小mismatch带来的影响了。
- 在接下来的每次迭代中,带入正确的(x,y)对:
对比与过去的没有修改的Cost Function,新的Cost Function有以下绿色的不同:
Structured SVM
1. 公式变换:
对于下面这个公式,因为我们需要求最小的C值,所以下面蓝色框框和绿色框框的公式是等价的。

这里后,可以写成:
Slack variable:松弛变量
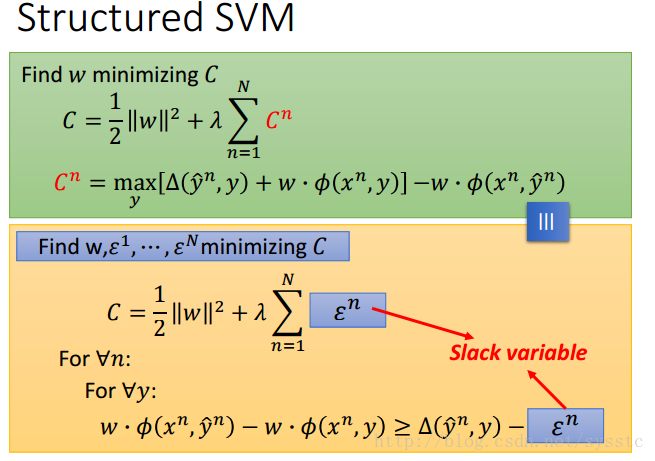
接下来,有一个constraint,就是y求到真实值的时候:

利用上述公式我们知道,每一个y≠y的真实值时都会产生一个限制(不等式),如下:
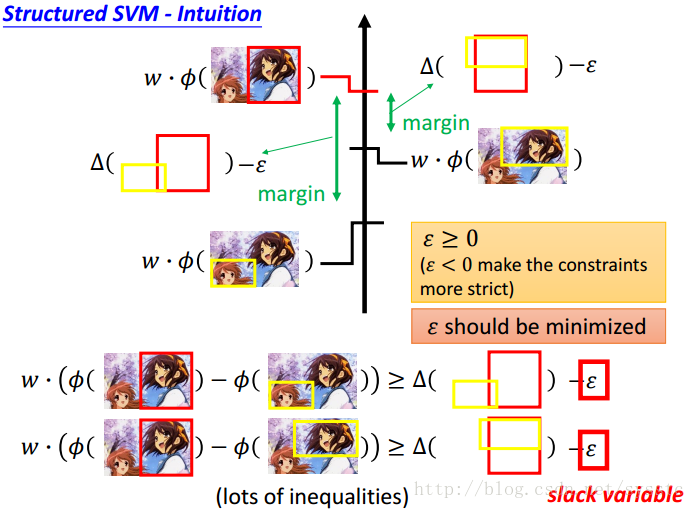
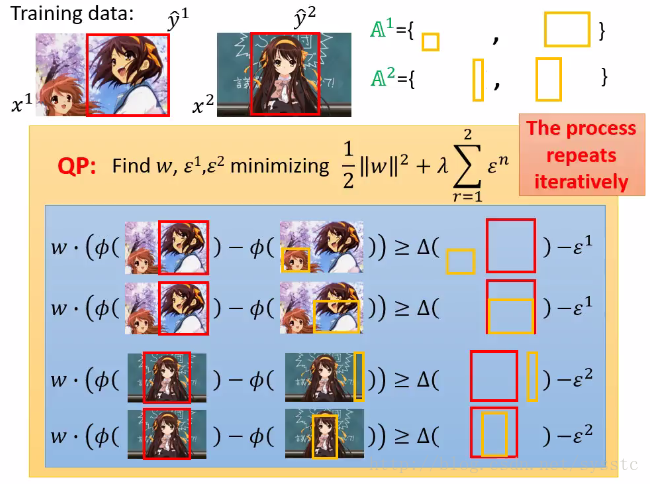
基于这些个限制(不等式),我们要求出C的最小值,如下:
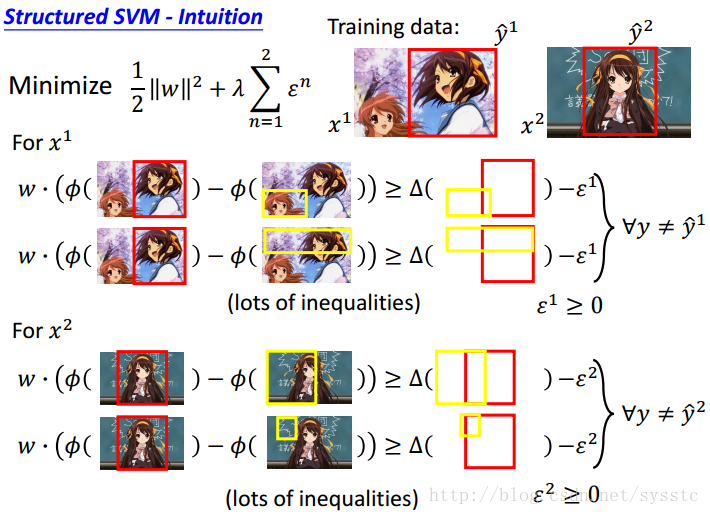
我们要找到一个w,和每一个example都有的ε,我们需要minimize这个function,并且满足下面的限制(不等式)

SVM:这个式子和SVM的式子是类似的
Structured SVM的API

Cutting Plane Algorithm for Structured SVM
1. 产生原因:
现在我们面临的问题就是太多constraints(不等式)了。我门将每个constraint都画在图上,为此,我们发现,只需要少数constraint其实就可以找到最小值了:
2. 解决方法
方法思想:
我们发现,在处理中,Red line是我们需要的两个constraint,而例如绿色的constraint即使忽略,也不会对结果产生其他影响。
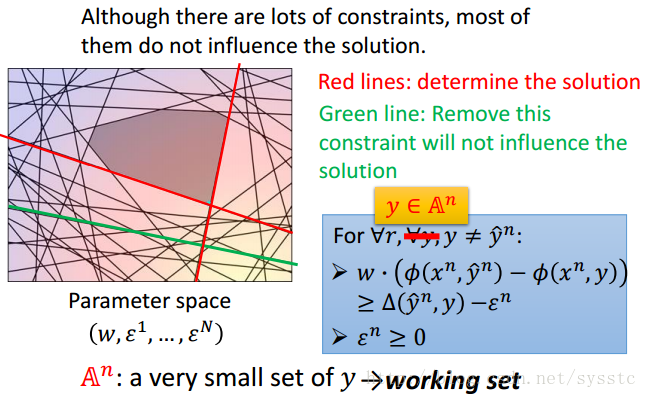
那么如何找到一个working set呢?
1. 为每一个example initialize 一个空的working set
2. 我们只需要考虑working set里面的y,重新得到一个w
3. 通过w,重新找一个working set成员(每找一次最小值,添加一个working set)
4. 再得到一个w,重新找到一个新的working set,接下来依次类推。
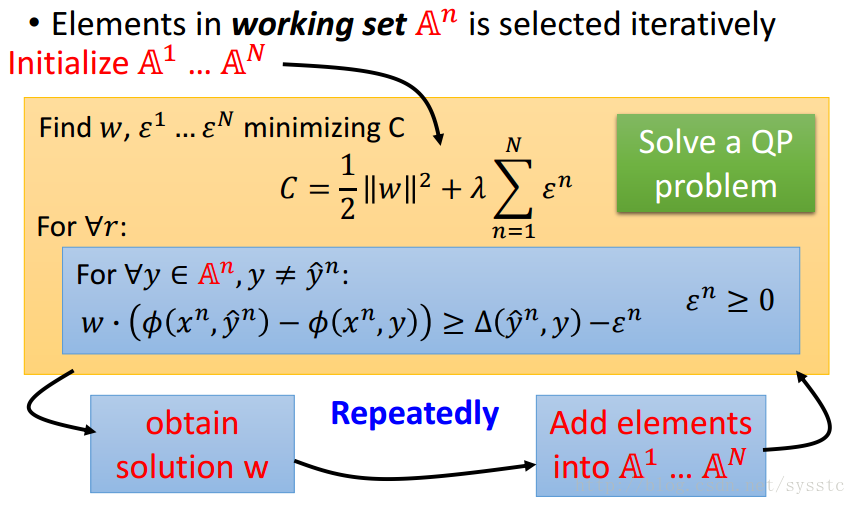
举例:
1. 假设A^n在初始的时候是空集合,也就是求解QP的时候没有限制,因此我们直接求解最小值,得到蓝色的点。
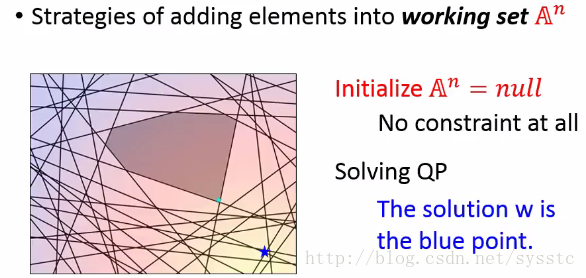
2. 接下来看看这么多constraint中,有什么是这个解满足不了的(如下图1的红线),我们从所有没有被满足的constraint中挑出最难处理的。

3. 例如我们找出最难处理的那条线(下图的红线),在这个图上就是表示和真实值举例最远的constraint。然后我们将这个红线添加到working set中,如下所示:

4. 接下来工具working set中的最小值,我们可以重新计算这个问题,因此我们找到一个最小值,即图上的蓝点。
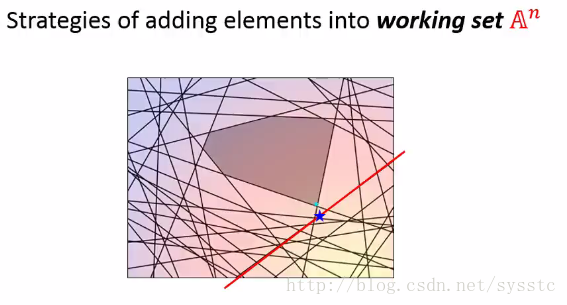
5. 接下来我们继续找到最难满足的constraint,然后根据现有的working set(以下两条红线),我们又可以找到一个最小值(即以下的蓝点点)。
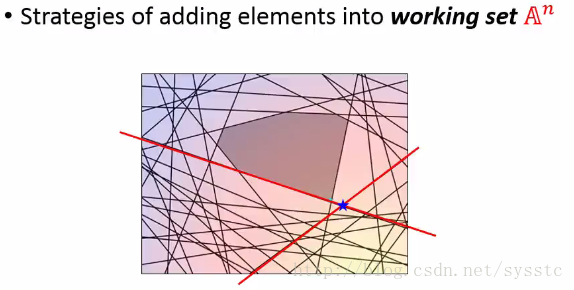
6. 接下来我们继续找一个constraint,找到一个最小值。
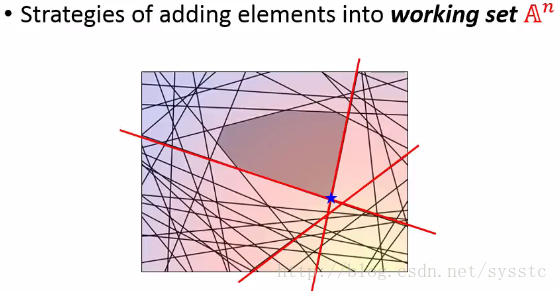
那么我们应该如何找到最难处理的constraint呢?
给定一个w’和ε’,如何求解最难处理的constraint呢?
首先,我们找到constraint是底下Constraint公式,那么最难处理的constraint就是底下这个Violate a Constraint公式(本来我们的大于等于,变成了小于),那么由于Violate会有很多个,因此我们需要一个公式Degree of Violation来定义violation的程度,即如果这项比较大则说明violate的程度越大(由于y head对于每一个y都是固定值且ε’不影响我们计算violate的值,因此,我们可以得到以下获得最大violate的值的公式):

Cutting Plane Algorithm的过程:

Cutting Plane Algorithm算法过程:
1. 我们这里的ε有一个constraint,即大于0,因此可以求出最小值为w = 0时,如下图所示:
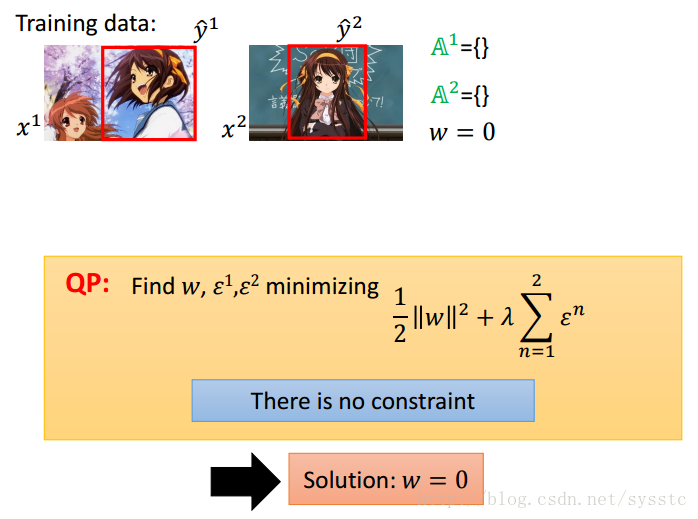
2. 接下来我们通过w = 0,找到一个most violate constraint,即计算下述方程:
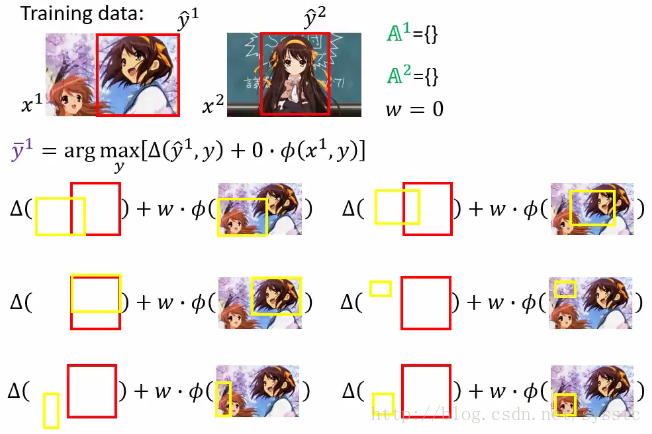
由于w = 0,接下来我们可以计算下面式子(y和y head没有交集时,答案均为1)
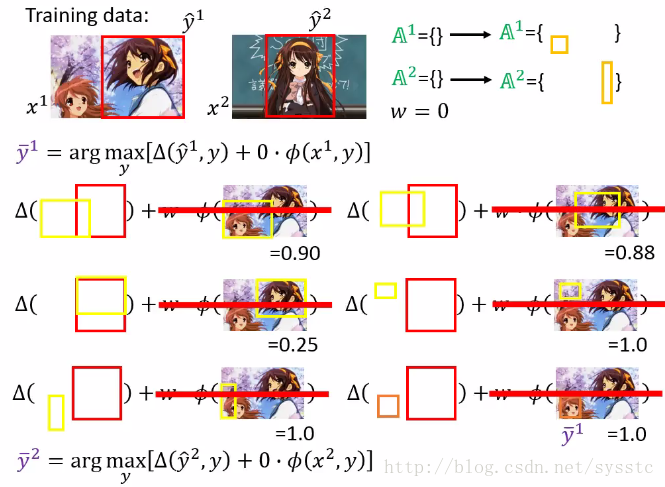
3. 接下来,我们通过给定的constraint求出C function的最小值,从而得到w = w1。
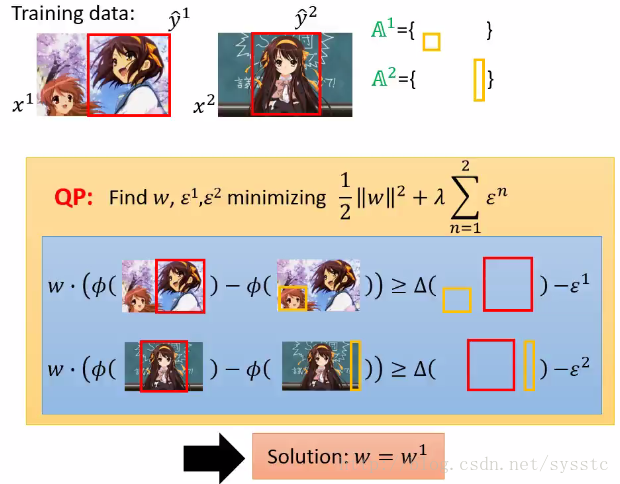
4. 接下来我们用w1,找出most violate的constraint
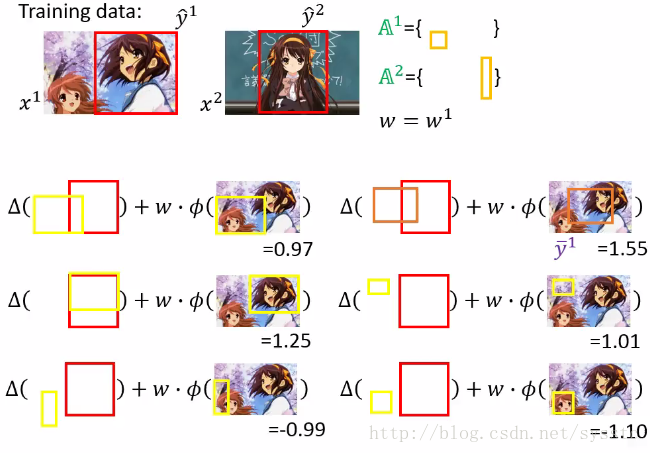
将most violate constraint放到我们的working set中:
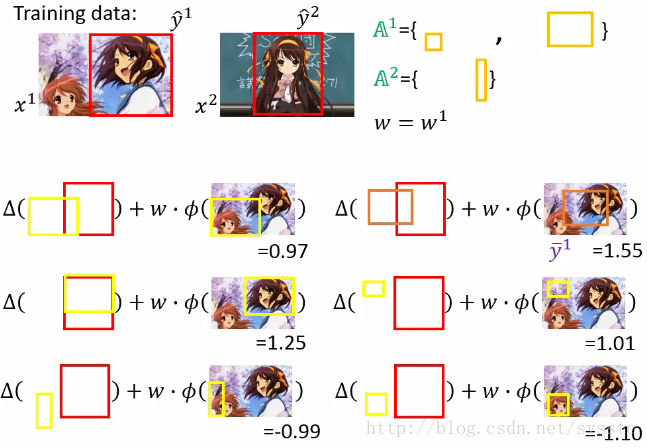
我们对A^2也做这个这个过程,也在working set中添加了一个constraint
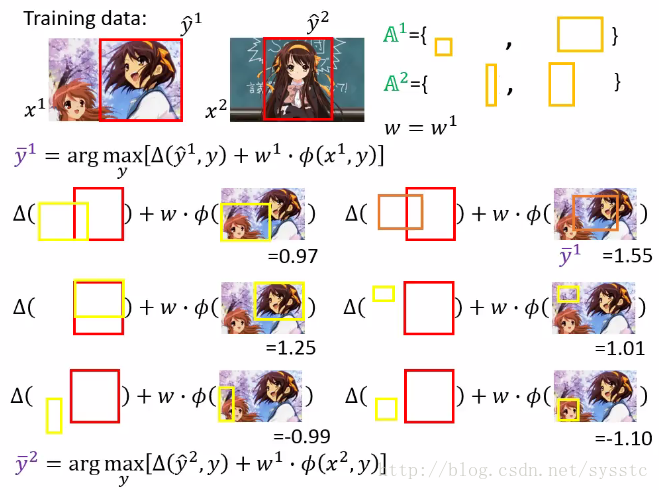
5. 接下来,我们只需要求解带有4个constriants方程就好,以此类推:
Multi class and binary SVM
Multi-class SVM
现在我们用Structured SVM来求解这个问题,首先,我们要思考三个problem
1. Evaluation:有K个class,有K个weight。

2. Inference:

3. Training:
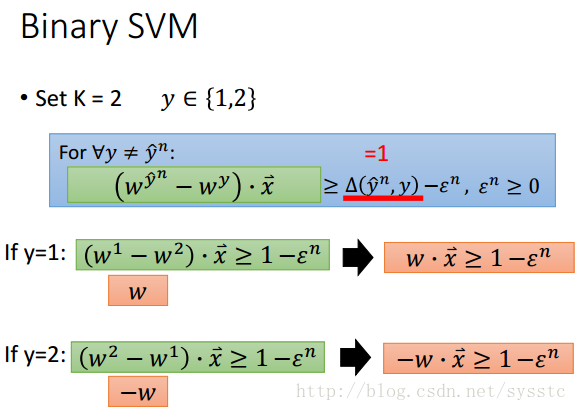
Binary SVM
定义:
Binary SVM其实就是K = 2的情况,我们假设如果y和y head不同则为1(因为Binary SVM其实就是有两个y的情况),我们假设y∈{1,2}
Beyond Structured SVM(open question)
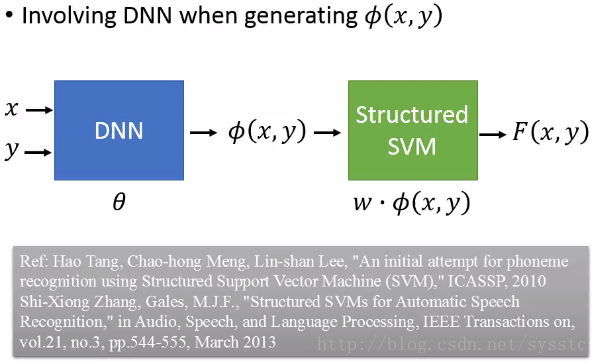
- Structured SVM是Linear的,因此我们需要找到比较好的feature function,我们可以用DNN的方法:
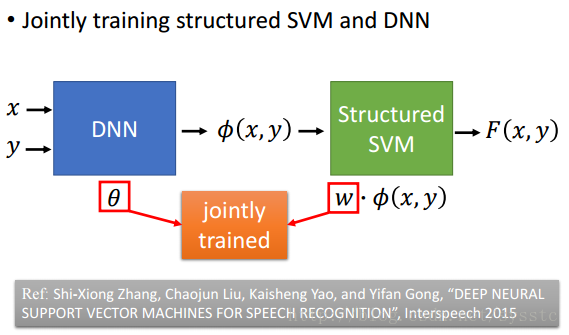
- 也可以一起Learn DNN和Structured SVM,把θ和w一起做Gradient Descent
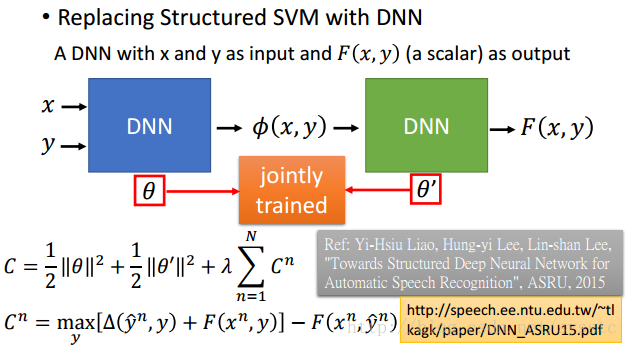
- 也可以用DNN替换Structured SVM,然后一起learn θ和θ’:











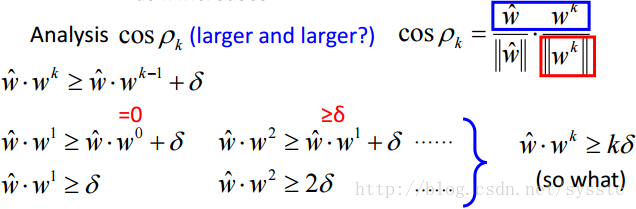



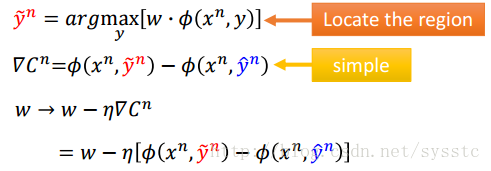

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








