机器学习复习（1）

K-means

k-means算法实际上就是通过计算不同样本间的距离来判断其之间的相近关系的，相近的就会放到同一个类别中去。

1. 首先需要选择一个k值，k值的选择对结果的影响很大。简单的说就是根据聚类的结果和k的函数关系判断k为多少的时候效果最好。

2. 然后需要选择最初的聚类点（或者叫质心），一般采用随机选择。这些点的选择会很大程度上影响到最终的结果。

3. 接下来计算数据集中所有的点与这些质心的距离，将其分到离其最近的质心那一类中去。需要计算每个簇的平均值，更新质心。反复执行，直到收敛。

   

举例理解：

假定有ABCD四个样本，将其聚成两类，如图：

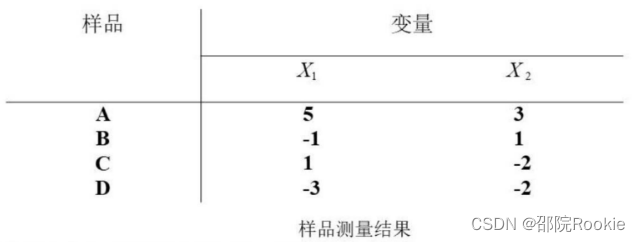
1. 读题意可知，聚成2类，K=2，为了实施平均聚类，将其分类为（AB）、（CD）两类，并计算中心坐标，中心坐标根据原始数据平均得出，如图所示：
2. 计算每个样品到各类中心的欧式距离，判断聚类是否合适。若不合适，则将其再分配给最近的类。对于重新分配的类，需要重新计算它们的中心坐标，然后进行下一次聚类结果的检测，只到完成聚类。
3. 先计算A到两个类（AB）、（CD）的平方距离：
   
   
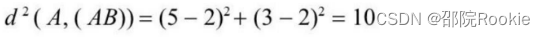
4. 由上可知d(A,(AB)＜d(A,(CD))，所以A不需要重新分配。
5. 再计算B到两个类（AB）、(CD)的平方距离：
   
   
6. 由于d（B,(AB)）>d（B,(CD)），因此（AB）聚类不合适，所以尝试把B分配到（CD）类，得到新的聚类(A),(B,C,D),更新后的如图所示：
7. 重新按上文计算平方距离的结果，如图所示：
8. 看上图可知，每个样品都分配到合适的聚类，因此聚类过程到此结束。

频繁项集

关联规则

关联规则（Association Rules） 反映一个事物与其他事物之间的相互依存性和关联性。如果两个或者多个事物之间存在一定的关联关系，那么，其中一个事物就能够通过其他事物预测到。
关联规则可以看作是一种IF-THEN关系。假设商品A被客户购买，那么在相同的交易ID下，商品B也被客户挑选的机会就被发现了。

• 置信度： 表示你购买了A商品后，你还会有多大的概率购买B商品。
  

• 支持度： 指某个商品组合出现的次数与总次数之间的比例，支持度越高表示该组合出现的几率越大。
  

• 提升度： 提升度代表商品A的出现，对商品B的出现概率提升了多少，即“商品 A 的出现，对商品 B 的出现概率提升的”程度。
  
  计算方法 如图所示：
  

Apriori算法

利用频繁项集生成关联规则。它基于频繁项集的子集也必须是频繁项集的概念。
Apriori算法就是基于一个先验 ：
如果某个项集是频繁的，那么它的所有子集也是频繁的。

算法流程

输入：数据集合D，支持度阈值α
　　 输出：最大的频繁k项集
　　　　1）扫描整个数据集，得到所有出现过的数据，作为候选频繁1项集。k=1，频繁0项集为空集。
　　　　2）挖掘频繁k项集
　　　　　　a) 扫描数据计算候选频繁k项集的支持度
　　　　　　b) 去除候选频繁k项集中支持度低于阈值的数据集,得到频繁k项集。如果得到的频繁k项集为空，则直接返回频繁k-1项集的集合作为算法结果，算法结束。如果得到的频繁k项集只有一项，则直接返回频繁k项集的集合作为算法结果，算法结束。
　　　　　　c) 基于频繁k项集，连接生成候选频繁k+1项集。
　　　　3） 令k=k+1，转入步骤2。
　　　　
频繁项集是支持值大于阈值（support）的项集。
项的集合称为项集。包含k个项的项集称为k-项集。项集的出项频率是包含项集的事务数，简称为项集的频率，支持度计数或计数。注意，定义项集的支持度有时称为相对支持度，而出现的频率称为绝对支持度。如果项集I的相对支持度满足预定义的最小支持度阈值，则I是频繁项集。

举例理解

第1次迭代：假设支持度阈值为2，创建大小为1的项集并计算它们的支持度。
我们可以看到，第4项的支持度为1 ，小于最小支持度2。所以我们将在接下来的迭代中丢弃{4} ，我们得到最终表F1。

第2次迭代：接下来我们将创建大小为2的项集（{4} 已经被丢弃了），并计算它们的支持度。F1中设置的所有项
再次消除支持度小于2的项集。在这个例子中{1，2}。
现在，让我们了解什么是剪枝，以及它如何使Apriori成为查找频繁项集的最佳算法之一。

剪枝:我们将C3中的项集划分为子集，并消除支持值小于2的子集。

第三次迭代：我们将丢弃{1,2,3}和{1,2,5}，因为它们都包含{1,2}。

第四次迭代：使用F3的集合，我们将创建C4。

因为这个项集的支持度小于2，所以我们就到此为止，最后一个项集是F3。
注：到目前为止，我们还没有计算出置信度。
使用F3，我们得到以下项集：
对于I={1,3,5}，子集是{1,3}，{1,5}，{3,5}，{1}，{3}，{5}
对于I={2,3,5}，子集是{2,3}，{2,5}，{3,5}，{2}，{3}，{5}

应用规则：我们将创建规则并将它们应用于项集F3。现在假设最小置信值是60%。
对于I的每个子集S，输出规则
S–>（I-S）（表示S推荐I-S）
如果：支持度(l)/支持度(S)>=最小配置值
{1,3,5}：

1. 规则1:{1,3}–>（{1,3,5}–{1,3}）表示1&3–>5
   置信度=支持度(1,3,5)/支持度(1,3)=2/3=66.66%>60%
   因此选择了规则1

2. 规则2:{1,5}–>（{1,3,5}–{1,5}）表示1&5–>3
   置信度=支持度(1,3,5)/支持度(1,5) =2/2=100%>60%
   因此选择了规则2

3. 规则3:{3,5}–>({1,3,5}–{3,5})表示3&5–>1
   置信度=支持度(1,3,5)/支持度(3,5)=2/3=66.66%>60%
   因此选择规则3

4. 规则4:{1}–>({1,3,5}–{1})表示1–>3&5
   置信度=支持度(1,3,5)/支持度(1)=2/3=66.66%>60%
   因此选择规则4

5. 规则5:{3}–>({1,3,5}–{3})表示3–>1和5
   置信度=支持度(1,3,5)/支持度(3)=2/4=50%<60%
   规则5被拒绝

6. 规则6:{5}–>({1,3,5}–{5})表示5–>1和3
   置信度=支持度(1,3,5)/支持度(5)=2/4=50%<60%
   规则6被拒绝