机器学习复习（2）

决策树

决策树原理

• 决策树：从训练数据中学习得出一个树状结构的模型。
• 决策树属于判别模型。
• 决策树是一种树状结构，通过做出一系列决策（选择）来对数据进行划分，这类似于针对一系列问题进行选择。
• 决策树的决策过程就是从根节点开始，测试待分类项中对应的特征属性，并按照其值选择输出分支，直到叶子节点，将叶子节点的存放的类别作为决策结果。
  举例：
  
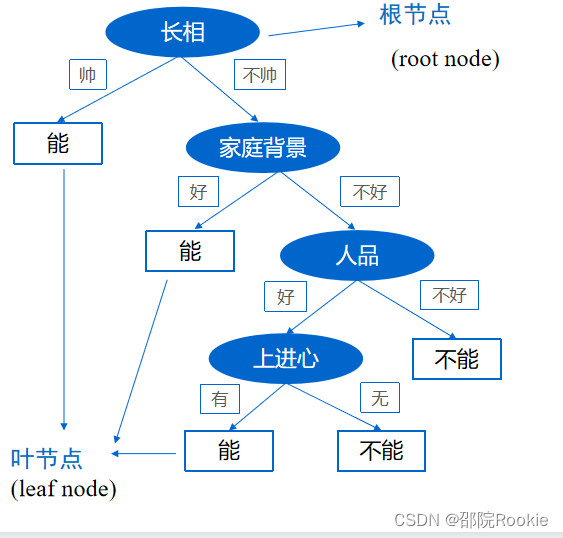
  决策树算法是一种归纳分类算法，它通过对训练集的学习，挖掘出有用的规则，用于对新数据进行预测。决策树算法属于监督学习方法。
  决策树归纳的基本算法是贪心算法，自顶向下来构建决策树。
  贪心算法：在每一步选择中都采取在当前状态下最好/优的选择。在决策树的生成过程中，分割方法即属性选择的度量是关键。
  

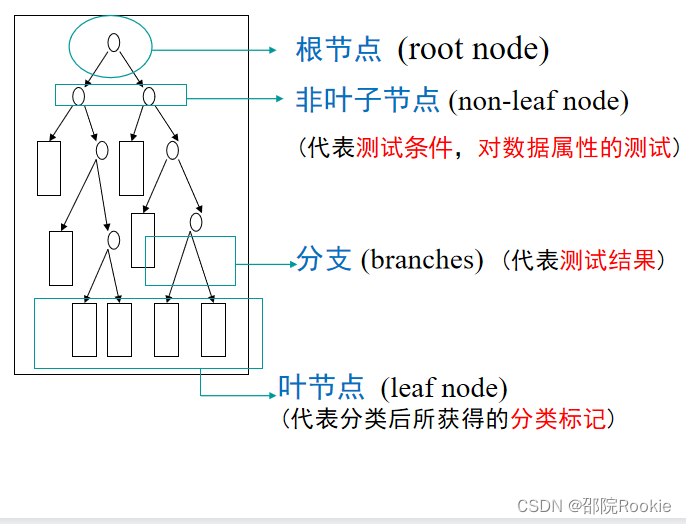
决策树的特点

优点

• 推理过程容易理解，计算简单，可解释性强。
• 比较适合处理有缺失属性的样本。
• 可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性，减少变量的数目提供参考。

缺点

1. 容易造成过拟合，需要采用剪枝操作。
2. 忽略了数据之间的相关性。
3. 对于各类别样本数量不一致的数据，信息增益会偏向于那些更多数值的特征。

相关算法比较：

ID3算法

其大致步骤为：

1. 初始化特征集合和数据集合；
2. 计算数据集合信息熵和所有特征的条件熵，选择信息增益最大的特征作为当前决策节点；
3. 更新数据集合和特征集合（删除上一步使用的特征，并按照特征值来划分不同分支的数据集合）；
4. 重复 2，3 两步，若子集值包含单一特征，则为分支叶子节点。
   信息熵：
   

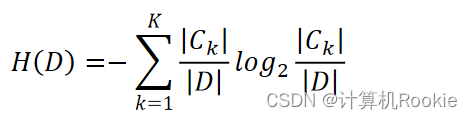
KNN算法

距离度量

欧氏距离

欧几里得度量（Euclidean Metric）（也称欧氏距离）是一个通常采用的距离定义，指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离。公式：

曼哈顿距离(Manhattan distance)

想象你在城市道路里，要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源， 曼哈顿距离也称为城市街区距离(City Block distance)。公式：

切比雪夫距离(Chebyshev distance)

二个点之间的距离定义是其各坐标数值差绝对值的最大值。
国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格，因此可以较有效率的到达目的的格子。上图是棋盘上所有位置距f6位置的切比雪夫距离。公式：

闵可夫斯基距离(Minkowski distance)

简称闵式距离
p取1或2时的闵氏距离是最为常用的
p=2即为欧氏距离，
p=1时则为曼哈顿距离。
当p取无穷时的极限情况下，可以得到切比雪夫距离

汉明距离(Hamming distance)

汉明距离是使用在数据传输差错控制编码里面的，汉明距离是一个概念，它表示两个（相同长度）字对应位不同的数量，我们以表示两个字之间的汉明距离。对两个字符串进行异或运算，并统计结果为1的个数，那么这个数就是汉明距离。

余弦相似度

两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。

假定A和B是两个n维向量，A是[A₁,A₂,…,A_n]，B是[B₁,B₂,…,B_n] ，则A和B的夹角的余弦等于：

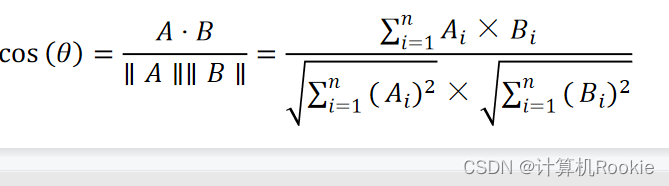
KNN算法简介

KNN可以说是最简单的分类算法之一，同时，它也是最常用的分类算法之一，注意KNN算法是有监督学习中的分类算法，它看起来和另一个机器学习算法Kmeans有点像（Kmeans是无监督学习算法上一篇写过），但却是有本质区别的。那么什么是KNN算法呢？

KNN全称是(K Nearest Neighbors)，意思是找K个最近的邻居，从这个名字我们就能看出一些KNN算法的蛛丝马迹了。K个最近邻居，K的取值肯定是至关重要的。那么最近的邻居又是怎么回事呢？

算法思路

算法的主要思路：
如果一个样本在特征空间中与k个实例最为相似(即特征空间中最邻近)，那么这k个实例中大多数属于哪个类别，则该样本也属于这个类别。

**对于分类问题：**对新的样本，根据其k个最近邻的训练样本的类别，通过多数表决等方式进行预测。
**对于回归问题：**对新的样本，根据其k个最近邻的训练样本标签值的均值作为预测值。
k近邻法的三要素：

1. k值选择。
2. 距离度量。
3. 决策规则。

算法流程：

1. 计算测试对象到训练集中每个对象的距离
2. 按照距离的远近排序
3. 选取与当前测试对象最近的k的训练对象，作为该测试对象的邻居
4. 统计这k个邻居的类别频次
5. k个邻居里频次最高的类别，即为测试对象的类别

其实啊，KNN的原理就是当预测一个新的值x的时候，根据它距离最近的K个点是什么类别来判断x属于哪个类别。如图所示，我们如果需要将绿色的圆点分类，那么它是属于哪一类呢（红三角还是蓝正方形）？

如上图所示，图中的正方形和三角形都是已经打好label的数据，分别代表不同的标签，而绿色的圆形代表的是待分类的数据。（K一般取奇数）

1. 若K=3（看里面的实线小圈），那么离绿色点最近的K个点（3个点）中有2个三角形和1个正方形，这三个点投票，三角形2/3，正方形1/3。故该待分类的点属于三角形类别。

2. 若K=5（外面的虚线大圈），那么离绿色点最近的K个点（5个点）中有2个红色三角形和3个蓝色正方形，这5个点开始投票，红色三角形2/5，蓝色正方形3/5，故该待分类的点属于蓝色正方形类别。