从感知机(Perceptron)到支持向量机(SVM)

$\textbf{duality chapter有错误，待修订}$

$\quad$ 本文会介绍感知机和支持向量机的原理，着重阐述这两个算法中的一些逻辑推导思路。

1.基础知识：函数距离(functional margins)和几何距离(geometrical margins)

假设$x\in\mathbb{R}^n$，那么显然$w^Tx+b=0$是一个超平面。通过推导，空间中的任意一点$x^{(i)}$到这个超平面的距离为

$$L=\frac{w^Tx^{(i)}+b}{||w||}$$

假设我们有样本点$A(x^{(i)},y^{(i)}),y^{(i)}\in\{1,-1\}$,

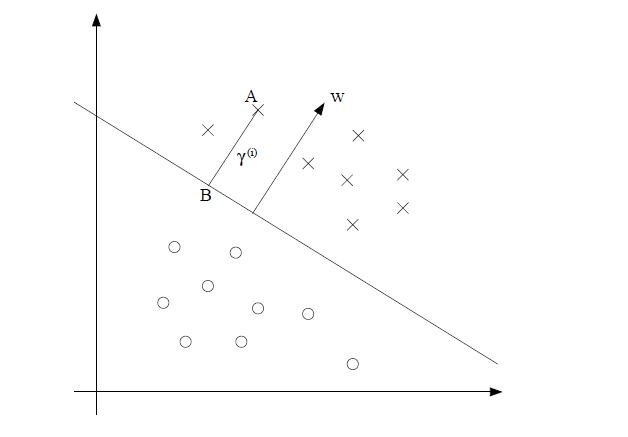
我们定义几何距离(geometrical margins)为

$$\gamma^{(i)}=y^{(i)}\left(\frac{w^Tx^{(i)}+b}{||w||}\right)$$

接着我们定义函数距离(functional margins)为

$$\hat\gamma^{(i)}=y^{(i)}(w^Tx^{(i)}+b)$$
这两个距离有什么特征呢？
① 函数距离可以表示分类的正确性和确信度：当 $w^Tx^{(i)}+b>0$时，说明样本A在超平面的上方，也就属于1类（记上图圆点为-1，叉点为1），如果此时 $y^{(i)}$=1,那么A样本分类正确， $\hat\gamma^{(i)}>0$；否则 $\hat\gamma^{(i)}<0$。
② 同倍数扩大或缩小w、b，超平面是不变的，函数距离会同等增减；而几何距离不变，因为点到固定平面的距离是不变的。
③ $\hat\gamma^{(i)}=\hat\gamma*||w||$

那这些特性有什么用呢？其实它们在感知计算法中起着重要作用

2.感知机(Perceptron)

利用特性①，我们可以判断样本点是否分类正确，最终画出一个超平面能把线性可分的数据正确分类（注意是线性可分的训练数据）；利用特性②，我们可以用误分类样本点的几何距离之和来表示模型的损失函数。
1、具体地，对于误分类点来说，$-y^{(i)}(w^Tx^{(i)}+b)>0$，所以所有误分类点到超平面的总距离是

$$-\frac1{||w||}\sum_{x^{(i)}\in M}y^{(i)}(w^Tx^{(i)}+b)$$
M为误分类的集合。这里我们可以直接省略 $\frac1{||w||}$，就得到感知机学习的损失函数 $L(w,b)=-\sum_{x^{(i)}\in M}y^{(i)}(w^Tx^{(i)}+b)$。
为什么可以直接省略 $\frac1{||w||}$?
（1）.因为感知机模型是以误分类点为驱动的，最后损失函数的值必然为零，即无误分类点。所以根据特性①，既然函数距离能判断样本点的分类正确性，我们何必用几何距离呢？实际上我们并不关心lost function具体数值的变化，我们只在乎还有没有误分类点。
（2）.去掉 $\frac1{||w||}$，我们得到的lost function是关于w,b的连续可导线性函数，可以用梯度下降法轻松地进行优化。

2、利用随机梯度下降法SGD，损失函数的梯度为

$$\nabla_wL(w,b)=-\sum_{x^{(i)}\in M}y^{(i)}x^{(i)}\\ \nabla_bL(w,b)=-\sum_{x^{(i)}\in M}y^{(i)}$$
随机选取一误分类点，对w,b进行更新： $$w\leftarrow w+\eta y^{(i)}x^{(i)}\\ b\leftarrow b+\eta y^{(i)}$$

3、算法：
给定数据集T，学习率$\eta$
（1）选取初值$w_0, b_0$
（2）根据函数距离选取误分类点
（3）更新$w, b$
（4）转至（2），直至没有误分类点

4、可证明对于线性可分数据集，感知机算法是收敛的，具体见《统计学习方法》。

3.支持向量机(SVM)

3.1.从感知机(Perceptron)到支持向量机(SVM)

感知机学习算法会因采用的初值不同而得到不同的超平面。而SVM试图寻找一个最佳的超平面来划分数据，怎么算最佳呢？我们自然会想到用最中间的超平面就是最好的。如下图

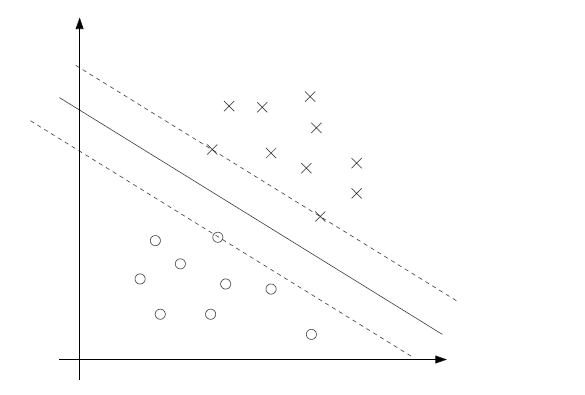
显然在SVM中我们不能在使用函数距离$\hat\gamma^{(i)}$来作为损失函数了，当我们试图使上图虚线之间的”gap”，最大自然要用几何距离。
我们定义

$$\gamma=\min_{i=1,...,m}\gamma^{(i)}$$ ,那么一个最优间距分类器可以写成
$$\begin{align}\max_{\gamma,w,b}&\quad\gamma\\ s.t.&\quad y^{(i)}\left(\frac{w^Tx^{(i)}+b}{||w||}\right)\geqslant\gamma,\quad i=1,...,m\end{align}$$
通过最大化 $\gamma$就可以找到最大的gap。
根据特性③，我们可以将上面的优化问题转化为 $$\begin{align}\max_{\gamma,w,b}&\quad\frac{\hat\gamma}{||w||}\\ s.t.&\quad y^{(i)}(w^Tx^{(i)}+b)\geqslant\hat\gamma,\quad i=1,...,m\end{align}$$
可是这个优化问题并不容易求解，我们期望目标函数是一个凸函数，这样优化起来就比较方便了。
这时注意到函数距离的特性②，我们可以直接让 $\hat\gamma=1$。Why?假设我们这个优化问题的最优解是 $w_{opt}，b_{opt}$，那么我们可以总是可以同倍数地调整 $w_{opt}，b_{opt}$使得 $\hat\gamma=1$，而此时最优超平面是不变的，所以上面的优化问题可以化成 $$\begin{align}\max_{\gamma,w,b}&\quad\frac{1}{||w||}\iff \min_{\gamma,w,b}\quad\frac12{||w||^2}\\ s.t.&\quad y^{(i)}(w^Tx^{(i)}+b)\geqslant1,\quad i=1,...,m\end{align}$$
这样SVM模型就转化为了一个二次规划问题（Quadratic Programming）。此时我们可以用matlab的一些工具来处理这个优化问题了，可是一旦数据量变大，计算就会变得很缓慢。所以我们此时把这个优化问题转化为一个拉格朗日对偶问题，此时不仅能简化计算，更能引入SVM中最重要的kernel概念。啥是拉格朗日对偶问题？为什么能简化计算？什么是kernel？为什么能引入kernel？好吧，我承认问题有很多，不过让我们一一来窥探。

3.2. Lagrange Duality

首先来看看wiki上对Lagrange Multipler和Lagrange Duality的说明
Lagrange Multipler：In mathematical optimization, the method of Lagrange multipliers is a strategy for finding the local maxima and minima of a function subject to equality constraints.

1.对于最简单的只有等式约束的规划问题，例如：

$$\begin{align}\min&\quad f(x,y)\\s.t.&\quad g(x,y)=c\end{align}$$
这个优化问题可以粗略地用函数等高线图来表示

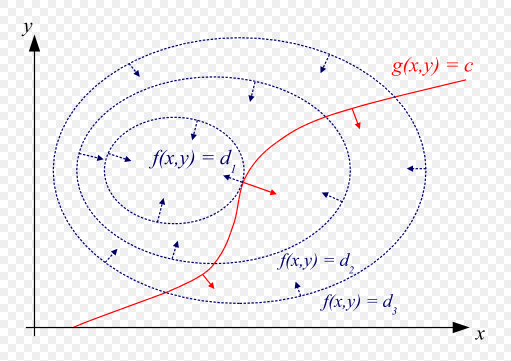
我们的目标就是要找到一点相切点$(x_0,y_0)$，使得$f(x,y)$达到最小值，因为梯度和等高线图是垂直的，所以$f(x,y)和g(x,y)$在点$(x_0,y_0)$上的梯度是平行的，此时，$\nabla_{x,y}f=-\lambda\nabla_{x,y}g$，其中$\nabla_{x,y}f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$，$\nabla_{x,y}g=(\frac{\partial g}{\partial x},\frac{\partial g}{\partial y})$，$-\lambda$就是两个向量的平行参数。
我们可以引入一个拉格朗日乘子$\lambda$得到Lagrange Function

$$L(x,y,\lambda)=f(x,y)+\lambda\left(g(x,y)-c\right)$$
那么令 $\nabla_{x,y}L=0$就是平行条件， $\nabla_{\lambda}L=0$就是原始问题的等式约束，这样就把原问题放到一个Lagrange Function中求解。

2.对于更一般的优化问题的原始问题，会有不等式约束例如：

$$\begin{gather}\min&f_0(x),\quad x\in \mathbb{R}^n\\s.t.&\quad f_i(x)\leqslant 0,\quad i=1,...,m\tag{1}\\&\quad h_j(x)=0,\quad j=1,...,p\tag{2}\end{gather}$$
原问题的定义域： $D=(\cap_{i=0}^mdomf_i)\cap( \cap_{j=1}^pdomh_j)$
可行点（feasible）： $x\in D$，且满足约束条件。
可行域：所有可行点的集合F。
最优化值： $p^*=\inf\{f_0(x)|f_i(x)\leqslant0,h_j(x)=0\}$（求下确界inf和求最小值min在这里是等价的）
注意定义域和可行域的差别：定义域和约束条件无关，一般来说定义域大于可行域。

步骤1：定义一个Lagrange函数为

$$\begin{gather}L(x,\lambda,\nu)=f_0(x)+\sum_{i=1}^m\lambda_if_i(x)+\sum_{j=1}^p\nu_jh_j(x)\\s.t.\quad\lambda_i\geqslant0 \tag{3}\end{gather}$$

假设对L函数在$x\in D$上逐点求下确界（参考boyd的《convex optimization》）的函数是

$$g(\lambda,\nu)=\inf_{x\in D}L(x,\lambda,\nu)$$ 这里的 $g(\lambda,\nu)$就是我们常说的 对偶函数（dual function），很明显它是一个关于 $\lambda，\nu$的线性函数。

如果我们把原问题的约束条件$\left(f_i(x)\leqslant 0，h_j(x)=0\right)$代入Lagrange function,那么对于原问题中可行域F中的任意可行点$\widetilde{x}$有

$$\sum_{i=1}^m\lambda_if_i(\widetilde{x})+\sum_{j=1}^p\nu_jh_j(\widetilde{x})\leqslant0$$
这个不等式可以推导出两个结果：
① 因为L函数后两项小于等于0，所以， $\max_{\lambda,\nu}L(x,\lambda,\nu)=f_0(x)$（注：这里的 $f_0(x)$是关于x的函数），进而 $$\min_x\max_{\lambda,\nu}L(x,\lambda,\nu)=p^*$$
我们称这个式子为对偶问题中的Primal Problem

② 因为L函数后两项小于等于0，所以

$$L(\widetilde{x},\lambda,\nu)=f_0(\widetilde{x})+\sum_{i=1}^m\lambda_if_i(\widetilde{x})+\sum_{j=1}^p\nu_jh_j(\widetilde{x})\leqslant f_0(\widetilde{x})$$
（注：这里的 $f_0(\widetilde{x})$是一个具体的值）
根据下确界的性质：一系列函数逐点下确界必然小于等于这一系列函数，有 $$g(\lambda,\nu)=\inf_{x\in D}L(x,\lambda,\nu)\leqslant L(\widetilde{x},\lambda,\nu)\leqslant f_0(\widetilde{x})$$
因为 $\widetilde{x}$是可行域F中的任意值，所以

⟹⟹g(λ,