【MWORKS专业工具箱系列教程】控制系列工具箱第一期：控制系统模型创建

最新推荐文章于 2024-09-24 10:19:23 发布

同元软控

最新推荐文章于 2024-09-24 10:19:23 发布

阅读量1.5k

点赞数 19

分类专栏：控制系列工具箱文章标签：工业软件建模仿真

本文链接：https://blog.csdn.net/sz_tongyuan/article/details/142327167

版权

控制系列工具箱专栏收录该内容

6 篇文章 0 订阅

订阅专栏

MWORKS控制系列工具箱包括基础控制系统工具箱、基于模型的控制器设计工具箱、系统辨识工具箱、鲁棒控制工具箱等，其中基础控制系统工具箱与基于模型的控制器设计工具箱是MWORKS控制系列工具箱的基础，下文将这两个工具箱合称为控制系统工具箱。

这两个工具箱面向经典控制和现代控制领域，为分析、设计和调节线性控制系统提供算法、模型和应用程序。支持将控制系统的构成环节指定为传递函数、状态空间或零极点增益模型，通过函数和应用程序，可实现对系统时域和频域响应的分析与可视化。提供交互式应用程序支持伯德回路整形和根轨迹方法来设计和调节补偿器参数。在现代控制方面，提供状态估计、LQG设计、极点配置等一系列功能函数。控制系统工具箱同时支持Modelica物理被控对象模型的线性化处理、分析、控制律设计和调节。

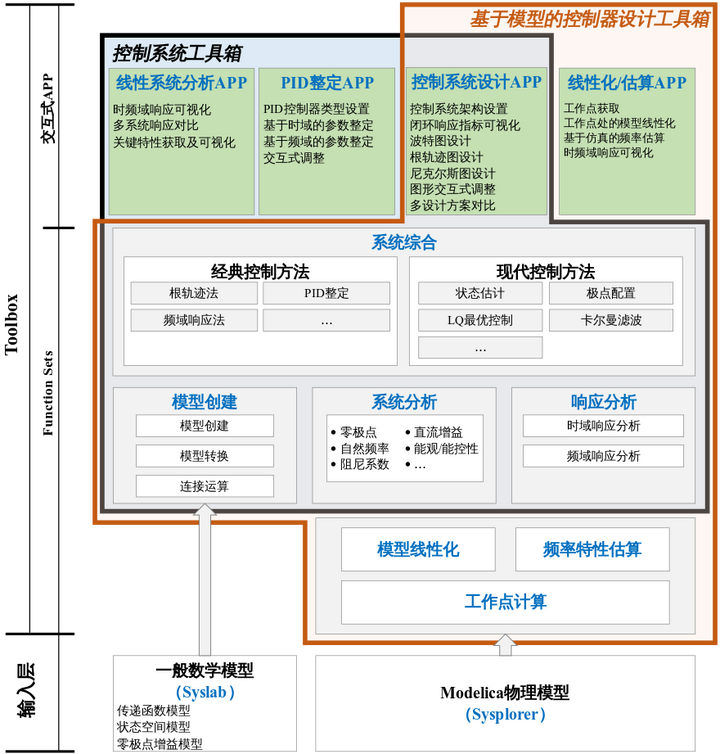
本工具箱教程以控制系统模型创建、分析与设计流程为主线，通过大量示例介绍MWORKS控制系统工具箱的功能和具体使用。包括10篇内容：

控制系统模型创建
控制系统模型转换
控制系统连接与化简
时域分析
频域分析
根轨迹分析
PID控制器设计
交互式控制系统设计APP
状态反馈设计
非线性模型的线性化

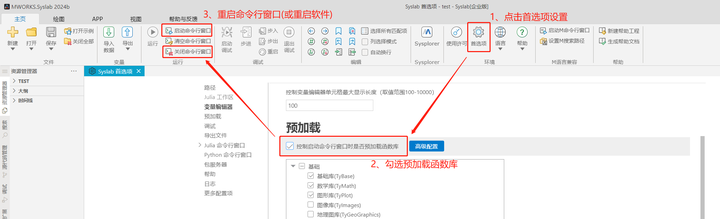
本教程代码均可直接复制到Syslab中运行，使用教程中代码前需参照下述方法加载函数库内容：

方法一：在Syslab的命令行窗口输入using TyControlSystems并回车(重启软件或命令行窗口后需重新输入)；
方法二：按照下图中的方法预加载函数库(设置好后每次启动软件默认加载)。

第一期：控制系统模型创建

大部分控制系统分析与设计的方法都需要假设系统的模型已知，而获得数学模型有两种方法：

从已知的物理规律出发，用数学推导的方式建立系统的数学模型
由实验数据拟合系统的数学模型（系统辨识）

线性系统一般可以用以下三种模型进行表示：

传递函数模型
状态空间模型
零极点增益模型

一、传递函数模型（tf）

连续时间动态系统一般以微分方程描述，而 LTI 系统则以定常系数线性常微分方程描述。假设系统的输入信号为 𝑢(𝑡) ，输出为 𝑦(𝑡) ，则 $n$ 阶系统的微分方程为：

${a_n}\frac{{{d^n}y\left( t \right)}}{{d{t^n}}} + {a_{n - 1}}\frac{{{d^{n - 1}}y\left( t \right)}}{{d{t^{n - 1}}}} + \cdots + {a_1}\frac{{dy\left( t \right)}}{{dt}} + {a_0}y\left( t \right) = {\kern 1pt} {b_m}\frac{{{d^m}u\left( t \right)}}{{d{t^m}}} + {b_{m - 1}}\frac{{{d^{m - 1}}u\left( t \right)}}{{d{t^{m - 1}}}} + \cdots + {b_1}\frac{{du\left( t \right)}}{{dt}} + {b_0}u\left( t \right){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {n \ge m} \right)$

系统输入量与输出量的 Laplace 变换之比即为其传递函数：

$G\left( s \right) = \frac{{Y\left( s \right)}}{{U\left( s \right)}} = \frac{{{b_m}{s^m} + {b_{m - 1}}{s^{m - 1}} + \cdots + {b_1}s + {b_0}}}{{{a_n}{s^n} + {a_{n - 1}}{s^{n - 1}} + \cdots + {a_1}s + {a_0}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} n \ge m$

传递函数可以表示成两个多项式的比值，在 Syslab 中，多项式可以用向量表示。将多项式的系数按 s 的降幂次序表示得到一个数值向量，分别用 𝑛𝑢𝑚 与 𝑑𝑒𝑛 表示分子、分母多项式，再利用 tf() 函数即可创建系统传递函数:

示例1：建立以下传递函数模型

$G\left( s \right) = \frac{{12{s^3} + 24{s^2} + 12s + 20}}{{2{s^4} + 4{s^3} + 6{s^2} + 2s + 2}}$

output:

 12s^3 + 24s^2 + 12s + 20
---------------------------
2s^4 + 4s^3 + 6s^2 + 2s + 2

连续时间传递函数模型

考虑如果传递函数分子分母多项式给出的不是完全展开的形式，而是若干因式的乘积，或者包括其他运算。这种情况可以定义Laplace算子： s = tf('s') ，然后用类似数学表达式的形式直接输入。

示例2：Syslab中建立传递函数模型

$G\left( s \right) = \frac{{3\left( {{s^2} + 3} \right)}}{{{{\left( {s + 2} \right)}^3}\left( {{s^2} + 2s + 1} \right)\left( {{s^2} + 5} \right)}}$

output:

                        3s^2 + 9
--------------------------------------------------------
s^7 + 8s^6 + 30s^5 + 78s^4 + 153s^3 + 198s^2 + 140s + 40

连续时间传递函数模型

离散时间动态系统一般以差分方程描述，LTI 系统则以定系数线性差分方程描述，对于离散SISO，设定采样周期为 T ，系统的输入为 𝑢(𝑖) ，输出为 𝑦(𝑖) ，则相应差分方程为：

${a_n}y\left( {i + n} \right) + {a_{n - 1}}y\left( {i + n - 1} \right) + \cdots + {a_1}y\left( {i + 1} \right) + {a_0}y\left( i \right) = {b_m}u\left( {i + m} \right) + {b_{m - 1}}u\left( {i + m - 1} \right) + \cdots + {b_1}u\left( {i + 1} \right) + {b_0}u\left( i \right)$

对上述方程进行 z 变换，得到离散系统的传递函数：

$H\left( z \right) = \frac{{Y\left( z \right)}}{{U\left( z \right)}} = \frac{{{b_m}{z^m} + {b_{m - 1}}{z^{m - 1}} + \cdots + {b_1}z + {b_0}}}{{{a_n}{z^n} + {a_{n - 1}}{z^{n - 1}} + \cdots + {a_1}z + {a_0}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} n \ge m$

在 Syslab 中，同样使用 tf() 函数创建离散系统传递函数，与连续传递函数不同的是，同时需要指定采样时间 ts 。

示例3：Syslab中建立离散系统传递函数模型，其采样周期为 T = 0.1s

$H\left( z \right) = \frac{{6{z^2} - 0.6z - 0.12}}{{{z^4} - {z^3} + 0.25{z^2} + 0.25z - 0.125}}$

output:

          6.0z^2 - 0.6z - 0.12
-----------------------------------------
1.0z^4 - 1.0z^3 + 0.25z^2 + 0.25z - 0.125

Sample Time: 0.1 (seconds)
离散时间传递函数模型

Tips: 针对离散时间系统模型，同样可以通过 z = tf('z'，ts) 定义 z 算子，再进行数学表达式的形式创建模型。

多变量系统模型的一种表述形式为：传递函数矩阵。这是单变量系统传递函数在多变量系统中的直接扩展，一般可写为：

其中 $G_{ij}$ 表示第 𝑖 路输入信号对第 𝑗 路输出信号的放大倍数

方式一： 通过创建的子传递函数构造MIMO系统传递函数矩阵

方式二： 通过分子、分母向量构成的矩阵构造MIMO系统传递函数矩阵

示例4：构建以下MIMO系统的传递函数矩阵

$G\left( s \right) = \left[ \begin{array}{cc} {\frac{{s - 1}}{{s + 1}}}&{\frac{{100}}{{\left( {s + 4} \right)\left( {s + 10.625} \right)}}}\\ {\frac{{s + 2}}{{{s^2} + 4s + 5}}}&{\frac{{s + 2}}{{{s^3} + 4s + 20}}} \end{array} \right]$

output:

输入 1 到输出 1
1.0s - 1.0
----------
1.0s + 1.0

输入 1 到输出 2
    1.0s + 2.0
-------------------
1.0s^2 + 4.0s + 5.0

输入 2 到输出 1
         100.0
-----------------------
1.0s^2 + 14.625s + 42.5

输入 2 到输出 2
     1.0s + 2.0
--------------------
1.0s^3 + 4.0s + 20.0

连续时间传递函数模型

示例5：构建以下离散MIMO系统的传递函数矩阵，采样时间为 𝑡𝑠=0.2𝑠

output:

输入 1 到输出 1
   1.0
----------
1.0z + 0.3

输入 1 到输出 2
-1.0z + 2.0
-----------
1.0z + 0.3

输入 2 到输出 1
   1.0z
----------
1.0z + 0.3

输入 2 到输出 2
   3.0
----------
1.0z + 0.3

Sample Time: 0.2 (seconds)
离散时间传递函数模型

二、状态空间模型（ ss ）

状态空间模型可以描述更广的一类控制系统，包括非线性系统、MIMO系统。针对连续时间 LTI 系统可以描述为：

针对连续时间 LTI 系统可以描述为：

$\left\{ \begin{array}{l} \dot x\left( t \right) = Ax\left( t \right) + Bu\left( t \right)\\ y\left( t \right) = Cx\left( t \right) + Du\left( t \right) \end{array} \right.$

针对离散时间 LTI 系统可以描述为：

$\left\{ \begin{array}{l} x\left[ {n + 1} \right] = Ax\left[ n \right] + Bu\left[ n \right]\\ y\left[ n \right] = Cx\left[ n \right] + Du\left[ n \right] \end{array} \right.$

示例6：构建下面的双输入双输出系统状态空间模型

output:

A = 
 -12.0  -17.2  -16.8  -11.9
   6.0    8.5    9.5    8.0
   5.0    8.7    3.5    6.0
  -6.0   -6.5   -9.7   -5.0
B = 
 2.5  0.1
 2.0  0.5
 3.0  1.0
 0.0  0.5
C =
 2.0  3.0   0.8   0.0
 0.5  0.56  0.3  -1.0
D =
 0.0  0.0
 0.0  0.0

连续时间状态空间模型

针对离散时间状态空间模型的创建，同样使用 ss 函数， G = ss(A,B,C,D,ts) ，增加 ts 指定采样时间即可

三、零极点增益模型（ zpk ）

零极点增益模型实际上是传递函数的一种特殊形式，其将系统表示为零点（Zeros）、极点（Poles）和增益（Gain）相乘的形式：

$G\left( s \right) = k\frac{{\prod\limits_{i = 1}^m {\left( {s + {z_i}} \right)} }}{{\prod\limits_{j = 1}^n {\left( {s + {p_j}} \right)} }} = k\frac{{\left( {s + {z_1}} \right)\left( {s + {z_2}} \right) \cdots \left( {s + {z_m}} \right)}}{{\left( {s + {p_1}} \right)\left( {s + {p_2}} \right) \cdots \left( {s + {p_n}} \right)}}$

其中： 𝑘 为系统增益， $-z_{i}\left( i = 1,2,\cdot\cdot\cdot m \right)$ 为系统零点， $-p_{j}\left( j=1,2,\cdot\cdot\cdot n \right)$ $-p_{j}\left( j=1,2,\cdot\cdot\cdot n \right)$ 为系统极点。

示例7：构建下面的零极点增益模型

$G\left( s \right) = \frac{{ - 2s}}{{\left( {s - 1 - i} \right)\left( {s - 1 + i} \right)\left( {s - 2} \right)}}$

output:

            s
-2---------------------
  (s^2 - 2s + 2)(s - 2)

连续时间传递函数模型

示例8：构建离散时间零极点增益模型，采样时间为𝑡𝑠=0.125𝑠

$H\left( z \right) = \left[ {\begin{array}{cc} {\frac{z}{{z - 0.3}}}\\ {\frac{{2\left( {z + 0.5} \right)}}{{\left( {z - 0.1 + i} \right)\left( {z - 0.1 - i} \right)}}} \end{array}} \right]$

output:

输入 1 到输出 1
      1.0z
1.0----------
   1.0z - 0.3

输入 1 到输出 2
        1.0z + 0.5
2.0--------------------
   1.0z^2 - 0.2z + 1.01

Sample Time: 0.125 (seconds)
离散时间传递函数模型

模型创建相关主要Syslab函数如下

函数及调用方式	说明
sys = tf(num,den)	返回变量为sys的连续时间传递函数
sys = tf(num,den,ts)	返回变量为sys的离散时间传递函数，其中ts表示为系统采样时间
s = tf('s')	定义Laplace算子，支持以有理多项式形式创建连续时间传递函数
z = tf('z',ts)	定义Z变换算子及其采样时间ts，支持以有理多项式形式创建离散时间传递函数
sys = zpk(z,p,k)	返回变量为sys的连续系统零极点增益模型
sys = zpk(z,p,k,ts)	返回变量为sys的离散系统零极点增益模型，其中ts表示为系统采样时间
sys = ss(A,B,C,D)	返回变量为sys的连续系统传递函数模型
sys = ss(A,B,C,D,ts)	返回变量为sys的离散系统传递函数模型，其中ts表示为系统采样时间