文章目录
前言
关联规则挖掘是数据挖掘领域中的重要技术,广泛应用于购物篮分析、推荐系统、医疗诊断等多个领域。本文将详细介绍两种经典的关联规则挖掘算法:Apriori算法和FpGrowth算法,包括它们的核心思想、实现细节、优缺点对比以及适用场景分析。
关联规则基本概念
-
关联规则:表示事物之间的关联关系,形式为X→Y,表示X出现时Y也倾向于出现。经典案例是"啤酒与尿布"的故事。
-
支持度(Support):衡量项集出现的频率,计算方式为包含该项集的交易数除以总交易数。例如:
- Support(A) = A出现的次数 / 总交易数
- Support(AB) = AB同时出现的次数 / 总交易数
-
置信度(Confidence):衡量规则的可靠性,计算方式为:
- Confidence(X→Y) = Support(XY) / Support(X)
-
提升度(Lift):衡量规则的有效性,计算方式为:
- Lift(X→Y) = Confidence(X→Y) / Support(Y)
- 提升度>1表示正相关,=1表示独立,<1表示负相关
-
频繁项集:支持度大于等于最小支持度阈值的项集。
1、什么是关联规则
现在有一个人,超市老板小红,她拿到了这组数据,想找出哪些商品是有关联的,关联是什么意思呢?
举个例子,比如,你想买个泡面,你一桶面不够吃,两桶吃不了,你是不是就想,要不我在顺便买个香肠?还不够!在加个蛋呢?实在不行,再加个鸡腿!
好了,现在你就明白了,泡面、香肠、鸡蛋、鸡腿,这4个商品可能就是关联的,如果超市把这几个放在一起,你在买泡面的时候,是不是一不小心就多消费了(万恶的资本家啊),你就会不由感受到,现在连泡面都吃不起了。
2、支持度
继续思考怎样找出这些关联商品,小红现在有4条数据记录(实际的超市,每天产生的数据可能上千,我们这里就简化一点,方便理解),小红很聪明,她认为,如果某一种商品组合(这个组合,可以是1个,或者2个,甚至3个以上的不同种类商品的组合),在整条数据库中出现的次数太少,那我就认为他们没有关联, 这个道理很显然,比如,商品组合AB,假如A是白酒,B是头孢(不要问我为什么超市会卖药,反正它现在就得卖→_→),这两个一起吃可能会中毒,那么你在买酒的时候肯定不会刻意去买头孢吧(不要说是给女朋友买的 ̄へ ̄,来自单身狗的怨念),换句话说,如果你买了A,大概率不会买B,甚至会刻意不去买B,那么AB同时出现在一条购物记录的次数必然不会太多,因此可以认为两者没有关联。
那小红又在想,这个商品组合出现的次数小于多少,我才认为它是无关联的呢?,这个次数可以随意规定,我们称为支持度。 但你试想一下,如果这个数定的太小,连 酒 和 头孢 您都认为有关联,然后 你把这两个摆在一起卖,显然不合适,算法意义也不大。如果定的太高,很多商品本来有关联,结果你定的太高,这些商品组合出现次数都不能满足这个数,那么这些商品组合你也就找不出来,算法也就失去了意义。所以这个值一定要取的合适才好。这个取值就称为 最小支持度。
对应于我们文中的例子,
A在四条记录中出现了2次,它的最小支持度min_support(A)=2,这是以它出现的次数作为最小支持度。
还可以用A出现的概率来表示,就是 A出现的次数 ÷ 总记录次数
A出现的次数是2,我们总共有4条数据,最小支持度也可以表示为:
min_support(A)=2/4=0.5
在看一下BE的最小支持度:
BE同时出现的次数为3次,总记录数依旧是4条,那
min_support(BE)=3 或 min_support(BE)=3/4 (在代码中用那种形式表示都可以,表示的意义是一样的)
3、置信度
小红又要开始想了(前面提到过她很聪明,手动狗头),只用次数大小来确定是否关联,是不是太草率了,假如你去买泡面,这个月钱快见底了(肯定啊,谁有钱会吃泡面),你打算买3或4包,到了地方,里面有很多口味的,比如麻辣,原味,三鲜,酸菜,但你就喜欢麻辣的,本来是想全买麻辣口味的,可惜的是每种口味都只剩2包了,无奈之下,你买了2包麻辣,还有1包酸菜的,走之前还拿了个蛋,,,这个时候你的这条购物信息是 {麻辣, 酸菜, 蛋},前面说了,我们不关心数量,只关心种类。
这个时候,虽然购物记录里面有 麻辣,和酸菜两种物品,但你要知道,你刚开始是想全买麻辣的,是因为麻辣的没了,才买了酸菜。虽然{麻辣,酸菜}同时出现了,且在计算支持度时,还提供了次数,可能会误认为麻辣和酸菜是 相关的,但其实你知道你是无奈才选的酸菜泡面,麻辣和酸菜并不是相关的,甚至顾客在买麻辣口味的时候,刻意不会去购买酸菜口味的泡面,它们是反相关的。
如果能计算出,顾客在买了麻辣的情况下,同时买了酸菜的概率多好啊,如果这个概率大,就表明顾客买了麻辣的,还要买酸菜的情况不是偶然,顾客就是同时喜欢吃这两种口味,每次买泡面,总是同时买这两种口味,两种口味是关联的。如果概率小,就表明顾客只喜欢其中一种口味,买酸菜是因为无奈之举,超市没货了。
现在就清楚了,我们算一下这个概率,很明显是条件概率的计算,用AB表示这两种商品,则 AB同时出现的次数 ÷ A出现的次数,就是顾客在买A的前提下,又买了B的概率,这个概率又称为 置信度,这个式子的意思表示,对于顾客 <买了A,同时又买了B的行为> 有多少自信,有多少把握,认为这个商品组合是有关联的。
和支持度类似,我们也得自己确定一个数,称为最小置信度,大于这个数就认为这个商品组合有关联。
下面对于文章给出的数据计算一下置信度:以BC为例,如:
BC同时出现的次数为2,B单独出现的次数为3
则置信度confidence(C–>B)=2/3,称为顾客 <买了C的情况下,又买了B的这个行为> BC具有关联性质的把握为2/3,换句话说,就是顾客买了C后,有 2/3 的概率去买B。
再算一下 顾客买了B的情况下,又买了C的置信度是多少
BC同时出现的次数依旧为2,C单独出现的次数为3
confidence(B–>C)=2/3,称为顾客 <买了B的情况下,又买了C的这个行为> 的可信度2/3,换句话说,就是顾客买了C后,有 2/3的概率去买B。
(当然,我们使用的数据太少,有些数据计算出来是100%,这完全是巧合,如果数据足够大,这个概率就就不会这样夸张了)
!!!要注意 :只有当这个商品组合的支持度大于它的最小支持度并且置信度大于最小置信度,我们才认为这个商品组合是强关联的,我们称这个商品组合为频繁项集。(为了简化代码,我仅仅只用了支持度,如果某种商品组合的支持度 大于 最小支持度,就认为是频繁项集。 并没有用到最小置信度,,如果读者有能力,可以自己做出改进,只需要在求频繁项集的时候,在保持这种商品组合的支持度大于最小支持度的情况下,同时保证该商品组合的置信度 大于 最小置信度 即可。)
(从公式可以看出,AB同时出现的次数其实就是AB的支持度,A单独出现的次数就是A的支持度,支持度可以用次数表示,也可以用频率表示,如用概率表示,则置信度confidence公式如下)

4、提升度
(也是一个度量某种商品组合是否为频繁项集的量(和支持度,置信度类似),大家可以了解一下,这个量我在代码中也没有体现,就是为了简化代码)
这时候小红还觉得不放心,她又思索了一下,发现这样一种情况:假如原来一个商品X,在总记录中出现的概率是80%(也就是支持度),但是XY两种商品同时出现的概率是50%,是不是在一定程度上,Y商品的出现反而降低了原来的商品X的销售额?
我们首先来看一个式子,

分析这个式子,对于P(AB),
- 如果A,B两个相互独立,即A发生不会影响到B,那么P(AB)=P(A)P(B),显然,最后这个式子结果为1
- 如果A,B不独立,即A发生会影响到B的发生,但是要注意,我们不能确定这个影响是什么类型,即A发生可能导致B发生的概率增加,也有可能A发生会导致B发生的概率减小。
上面这个式子就是提升度计算公式,即提升度 Lift(A–>B)为:

例子,我们来看一下文章给出的数据,比如BC:
BC同时出现的次数为2,支持度support(B–>C)=2/4
C单独出现的次数为3,支持度support(C)=3/4
B单独出现的次数为3,支持度support(B)=3/4
由以上数据可计算出B–>C的置信度,
confidence(B–>C)= support(B–>C) ÷ support(B) = 2/3
则提升度:
Lift(B–>C)=confidence(B–>C) ÷ support( C) = 8/9
因为提升度小于1,所以可以确定,购买B时,会降低对C的购买,如果计算出来提升度大于1,说明购买B时,会促进C的购买。
Apriori算法思路
Apriori算法是最早提出的关联规则挖掘算法,基于以下两个重要性质:
- Apriori性质1:如果一个项集不是频繁的,则它的所有超集也一定不是频繁的
- Apriori性质2:如果一个项集是频繁的,则它的所有子集也一定是频繁的
算法通过"连接"和"剪枝"两个步骤迭代产生候选项集,然后扫描数据库计算支持度,找出频繁项集。
如何实现算法
1、找出所有频繁项集。
就是该商品组合的支持度 大于 最小支持度
2、由频繁项集确定下一组候选集
过程如图所示

(1)第一次扫描
首先,求第一次扫描数据库后的候选集。
从图中可以看出,第一次扫描后,可以求出单个商品的支持度(图中支持度用出现次数表示),这个表称为第一次候选集,即下图所示:

在第一次候选集基础上,求出第一次频繁项集,频繁项就是该商品的支持度 大于 最小支持度,支持度选择时随意的,在这里取最小支持度为 min_support=2
那么第一次频繁项集就是第一次候选集中,支持度大于或等于2的所有商品集合。即下表,(把 D 商品从表中去除了,因为它的支持度小于2)

(2)第二次扫描
先求出第二次的候选集。
即在第一次频繁项集的基础上,找出第二次候选集,对商品进行组合,形成一个2元组,4种商品,不同组合有C42种,即 4x3=12 种,形成的表称为第二次候选集表。如下图

在求第二次频繁项集
对于上表,求出这两种商品同时出现在总记录中的次数(即求支持度),然后去掉支持度小于2的商品组合,形成的表即为第二次频繁项集。如下表

(3)第三次扫描
先求出第三次的候选集。
即在第二次频繁项集的基础上,找出第三次候选集。
就是将原来的2元组,拓展为3元组,怎么拓展呢?
设K为第K次扫描,要求第K个候选集,找出上一次扫描的频繁项集,然后观察里面的记录,对于里面的每个记录,前(K-2)个前缀相同的,归为一类,在同一类别中进行合并。
比如 这第三次扫描,要求出它的候选集,先找出上次扫描形成的第二次频繁项集表,里面有4条记录,分别为,AC,BC,BE,CE,这些记录中,前(K-2)个前缀,就是前(3-2)个前缀,也就是第一个前缀相同的归为一类,接着在属于同一类的记录中,进行合并,比如BC,BE,它门的第一个前缀都是B,那么在这一类中,把它门合并起来就形成了BCE。还剩下AC、CE,它门第一个前缀不相同,也没有其他元素和它门相同,那么就不用去管了。如果你非要合并,把AC、CE合并为ACE,我们看一下ACE的子集,它的子集是{AC、CE、AE},可以看出AC、CE确实是频繁项集,但是AE呢,你在求第二次的候选集时,因为AE的支持度小于2,你把它去除了,那么ACE也必然不是频繁项集。(Apriori定律1 :如果某商品组合小于最小支持度,则就将它舍去,它的超集必然不是频繁项集。)
第四次扫描和前两次原理一样
(4)减枝
-----------在这里要说明一下减枝的概念
比如刚才新形成的BCE这个组合,它的子集是{BC、CE、BE},显然BC和CE本来就是一个频繁项集,但是CE呢,我们必须对比上一次频繁项集中的元素,也就是第2次频繁项集的元素,如果CE不是第二次频繁项集的元素,那么就把新形成的 BC E 这个元素给 “减去”,也就是减枝,这一点我在代码中有体现,具体请看后面的代码。
代码实现
'''
#请从最后的main方法开始看起
Apriori算法,频繁项集算法
A 1, B 2, C 3, D 4, E 5
1 [A C D] 1 3 4
2 [B C E] 2 3 5
3 [A B C E] 1 2 3 5
4 [B E] 2 5
min_support = 2 或 = 2/4
'''
def item(dataset): #求第一次扫描数据库后的 候选集,(它没法加入循环)
c1 = [] #存放候选集元素
for x in dataset: #就是求这个数据库中出现了几个元素,然后返回
for y in x:
if [y] not in c1:
c1.append( [y] )
c1.sort()
#print(c1)
return c1
def get_frequent_item(dataset, c, min_support):
cut_branch = {} #用来存放所有项集的支持度的字典
for x in c:
for y in dataset:
if set(x).issubset(set(y)): #如果 x 不在 y中,就把对应元素后面加 1
cut_branch[tuple(x)] = cut_branch.get(tuple(x), 0) + 1 #cut_branch[y] = new_cand.get(y, 0)表示如果字典里面没有想要的关键词,就返回0
#print(cut_branch)
Fk = [] #支持度大于最小支持度的项集, 即频繁项集
sup_dataK = {} #用来存放所有 频繁 项集的支持度的字典
for i in cut_branch:
if cut_branch[i] >= min_support: #Apriori定律1 小于支持度,则就将它舍去,它的超集必然不是频繁项集
Fk.append( list(i))
sup_dataK[i] = cut_branch[i]
#print(Fk)
return Fk, sup_dataK
def get_candidate(Fk, K): #求第k次候选集
ck = [] #存放产生候选集
for i in range(len(Fk)):
for j in range(i+1, len(Fk)):
L1 = list(Fk[i])[:K-2]
L2 = list(Fk[j])[:K-2]
L1.sort()
L2.sort() #先排序,在进行组合
if L1 == L2:
if K > 2: #第二次求候选集,不需要进行减枝,因为第一次候选集都是单元素,且已经减枝了,组合为双元素肯定不会出现不满足支持度的元素
new = list(set(Fk[i]) ^ set(Fk[j]) ) #集合运算 对称差集 ^ (含义,集合的元素在t或s中,但不会同时出现在二者中)
#new表示,这两个记录中,不同的元素集合
# 为什么要用new? 比如 1,2 1,3 两个合并成 1,2,3 我们知道1,2 和 1,3 一定是频繁项集,但 2,3呢,我们要判断2,3是否为频繁项集
#Apriori定律1 如果一个集合不是频繁项集,则它的所有超集都不是频繁项集
else:
new = set()
for x in Fk:
if set(new).issubset(set(x)) and list(set(Fk[i]) | set(Fk[j])) not in ck: #减枝 new是 x 的子集,并且 还没有加入 ck 中
ck.append( list(set(Fk[i]) | set(Fk[j])) )
#print(ck)
return ck
def Apriori(dataset, min_support = 2):
c1 = item (dataset) #返回一个二维列表,里面的每一个一维列表,都是第一次候选集的元素
f1, sup_1 = get_frequent_item(dataset, c1, min_support) #求第一次候选集
F = [f1] #将第一次候选集产生的频繁项集放入 F ,以后每次扫描产生的所有频繁项集都放入里面
sup_data = sup_1 #一个字典,里面存放所有产生的候选集,及其支持度
K = 2 #从第二个开始循环求解,先求候选集,在求频繁项集
while (len(F[K-2]) > 1): #k-2是因为F是从0开始数的 #前一个的频繁项集个数在2个或2个以上,才继续循环,否则退出
ck = get_candidate(F[K-2], K) #求第k次候选集
fk, sup_k = get_frequent_item(dataset, ck, min_support) #求第k次频繁项集
F.append(fk) #把新产生的候选集假如F
sup_data.update(sup_k) #字典更新,加入新得出的数据
K+=1
return F, sup_data #返回所有频繁项集, 以及存放频繁项集支持度的字典
if __name__ == '__main__':
dataset = [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]] #装入数据 二维列表
F, sup_data = Apriori(dataset, min_support = 2) #最小支持度设置为2
print("具有关联的商品是{}".format(F)) #带变量的字符串输出,必须为字典符号表示
print('------------------')
print("对应的支持度为{}".format(sup_data))

算法优缺点分析
优点:
- 原理简单直观,易于理解和实现
- 采用逐层搜索的迭代方法,算法思路清晰
- 适合处理小规模数据集
缺点:
- 需要多次扫描数据库,I/O负载大
- 可能产生大量候选项集,尤其是当最小支持度较低时
- 对大数据集效率较低,时间复杂度高
FpGrowth算法思路
FpGrowth算法,全称:Frequent Pattern Growth—-频繁模式增长,该算法是Apriori算法的改进版本,我们知道Apriori算法为了产生频繁模式项集,需要对数据库多次扫描,当数据库内容太大,那么算法运行的时间是难以忍受的,因此有人提出了FpGrowth算法,只须扫描数据库两次即可求出频繁项集,大大的缩减了扫描数据库的时间
FpGrowth(Frequent Pattern Growth)算法是针对Apriori算法缺点的改进算法,主要思想是:
- 通过构建FpTree(频繁模式树)压缩数据库
- 只需扫描数据库两次即可完成挖掘
- 采用分治策略,将挖掘频繁项集的问题转化为递归地挖掘条件模式
如何实现算法
1、构建FpTree
FpGrowth算法最经典的思想就是构建一颗树来压缩大量数据记录,如何把多条数据记录压缩到一颗树中呢?用一个例子就可以清晰表达出这个思想。
我们以下面的数据记录为例:
(假设某超市有6种商品,以下是5个顾客的购买情况,我们依旧不关心购买数量,只关心购买种类)
| 顾客ID | 购买种类(Item) |
|---|---|
| T1 | 牛奶,面包 |
| T2 | 面包, 尿布, 啤酒, 鸡蛋 |
| T3 | 牛奶, 尿布, 啤酒, 可乐 |
| T4 | 面包 ,牛奶, 尿布, 啤酒 |
| T5 | 面包, 牛奶, 尿布, 可乐 |
为了方便程序实现,把这些商品种类替换为字母表示
| 牛奶 --> a | 面包 --> b | 尿布 --> c |
| 啤酒 --> d | 可乐 --> e | 鸡蛋 --> f |
替换后数据记录如下:
| 顾客ID | 购买种类(Item) |
|---|---|
| T1 | a, b |
| T2 | b, c, d, f |
| T3 | a, c, d, e |
| T4 | b, a, c, d |
| T5 | b, a, c, e |
【注意】:为了方便程序实现简化代码,我依旧只使用支持度来判断。
- 对数据库进行第一次扫描,找出所给数据记录中商品的种类,并且对每一种商品出现的次数进行计数,即可得出第一次扫描结果,结果如下:
(这里有个细节,我们求出每种商品出现的次数后,需要按照 出现次数 的大小,由大到小排列,如果出现次数相同,则先后顺序无所谓)

这个时候,就要用到支持度的概念了,我们知道,如果某一种商品组合(这个组合,可以是1个,或者2个,甚至3个以上的不同种类商品的组合),在整条数据库中出现的次数太少,那我就认为他们没有关联, 这个道理很显然。就是对应与Apriori两个定理之一,非频繁项集的超集一定不是频繁项集。
所以,这里我设置最小支持度为3,只要支持度大于等于3,我就认为这个商品组合是频繁项集。
因此,对于上表,去除不符合条件的项集 e 和 f,结果如下:

- 第二次扫描数据库,开始创建FpTree, 初始时,先创建一个根节点,记为null。
首先对于每一条数据记录,先对里面的商品种类按照 ==“某种顺序” ==排序,(这个某种顺序是,在第一次扫描数据库后,按照其商品出现次数,由大到小排列后,其对应的商品种类顺序。这个例子有点巧合,按照各个商品出现次数由大到小排序后,商品种类的顺序恰好是字母顺序 abcdef ,在真实的数据记录中,不一定是这样。比如,现在有一个新的数据记录,进行统计后,发现,a出现2次,b出现5次,c出现10次,d出现1次,e出现15次,f出现6次,那么,按照出现次数由大到小排序后,这个 “某种顺序” ,就是 ecfbad ,每条数据记录都要按照这个奇怪的顺序排列,不再是按照字母表顺序了 )。
现在对于第一条已经排好序的记录,就是(a,b)这条记录,先创建一个节点,命名为a,将其插入根节点null下,并且在这个节点内,设置一个count变量,令count=1,接着在创建一个节点,命名为b,将其插入节点a下,同样的,在节点b内,令它的count=1,至此,第一条记录扫描完成,形成的树见下图:

对于第二条已经排好序的记录,就是(b, c, d, f),我们要先去除那些不是频繁项集的字母,也就是f,f的支持度为1,比最小支持度小。过滤掉这些非频繁项集后,第二条记录变为了(b, c, d)。现在开始插入节点,从根节点开始看,由于根节点的孩子中没有b这个孩子,那么现在创建一个节点b,把它插入根节点下,令这个b节点的count=1。在创建一个c节点,插入刚才的b节点下,令c节点count=1。在创建一个d节点,将其插入刚才的c节点下,令d节点的count=1。至此第二条记录扫描完毕,此时FpTree的结构如下图:

对于第三条已经排好序的记录,就是(a, c, d, e)同样的,我们要过滤到非频繁项集,所以第三条记录变为了(a, c, d)。现在开始插入节点,从根节点开始看,发现根节点null的孩子中有a节点,那么我们就不创建新节点了,我们将这个的a节点的count + 1,即现在a节点的count=2。接着看a节点的孩子中有没有c节点,发现找不到,则创建一个c节点,令count=1,将其插入a节点下。最后,创建一个d节点,令count=1,将其插入刚刚创建的c节点下。至此,第三条记录扫描完毕,现在的FpTree形状如下:

对于第四条已经排好序的记录,就是(a, b, c, d),逻辑同第三条
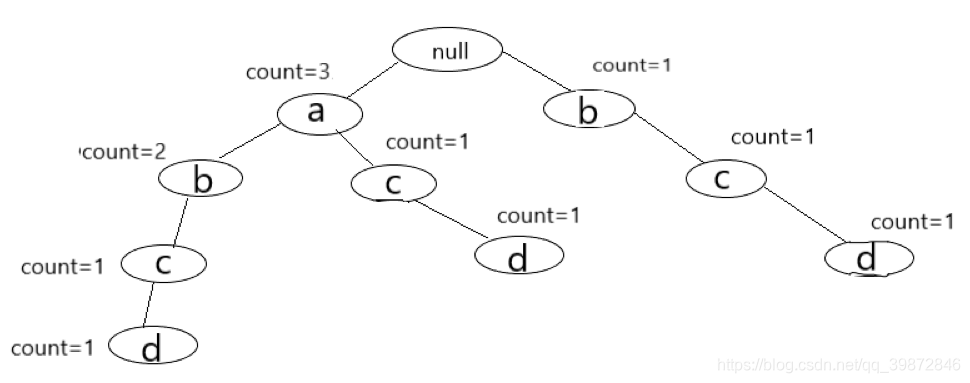
第5条排好序的数据记录,即(a, b, c, e)

经过上面的学习,我们就可以大致猜出,每个节点所包含的信息有哪些了,请看下图:

- idName:节点名字
- childs: 指向该节点所有孩子节点的地址
- parent: 指向该节点的父亲节点(在挖掘关联规则时,需要找到父亲节点)
- nextCommonId: 指向下一个节点,这个节点与该节点名字相同(用于构造线索,文章下文有说明)
- idCount: 就是在刚才构造这颗树时,我们说的count,用于计数
2、FpTree线索的构造
刚才我们已经构建出了FpTree,这个树有什么意义呢?
我们知道在最开始的数据记录中,数据松散不堪,每条记录中,各个商品只出现1次。那么经过这样的变换,我们可以通过某种特殊方式,遍历这个树,就可以还原最开始的数据集,这个特殊方法是
- 对这颗树,我们从根节点开始,随意找一条路径,这条路径的结尾节点必须是尾节点(尾节点就是,该节点没有孩子节点),那么这条路径就是一条记录,将这条记录取出后,别忘了对这条路径上的每个节点的count-1。
- 在这个过程中,如果某个节点的count=0了,那么就移除这个节点。
只要按照这个方法,就可以完美还原出初始的数据集了,显然,这种树状的数据存储方式极大的压缩了原来的数据集,非常实用。
但是,您应当已经注意到了,这颗树的节点,有许多名字相同的节点,其实,在最后,我们对这个树进行挖掘关联规则时,您就知道这个现象的用处了。
事实上,您如果把相同名字节点的count加起来,其结果就是该商品在总数据记录中出现的总次数。比如 b节点,在FpTree中有2个节点,其count值相加,即 3 + 1 = 4 ,正好是b在总记录中出现的次数。其他节点也是如此。
为了方便我们后续用这颗树挖掘关联规则,我们需要建立一个线索,把这些节点名字相同的节点用链表串起来。
我们可以创建一个表头,以它为链表的头部,把名字相同的节点串起来。

3、挖掘关联规则
频繁模式树FpTree建好后,线索也建立了,现在开始挖掘关联规则。
注意:在这里,我只认为支持度大于最小支持度就认为它是频繁项,最小支持度依旧为3。

上图就是第一次扫描数据库后,按照商品出现次数排序后的表格,挖掘关联规则时,要首先从表尾开始挖掘。
- 在这个例子中,就是从d节点开始,根据我们创建的线索表,可以很轻松的找出所有相同节点,然后可以写出这些节点所在的节点分支,即(a,b,c,d :1),(a,c,d :1),(b,c,d :1),后面的数字 1 是每条分支的最后一个节点的count值。这里要注意一下,虽然 a 出现了 4 次(即a的count=4),但是 a,b,c,d 这个整体只出现了 1 次,这取决与,在这条分支上,某个节点的最小count值。
现在,我们去除d节点,(直接把所有的d节点删除),那么就可以得到d的前缀节点(d的前缀节点就是d节点前面的节点),即{ (a,b,c :1),(a,c :1),(b,c :1) }, 还要注意一下,这里的数字 ”1“,依旧是原来的d节点的count值,不是c节点的count值。
好了,做到这步,我们其实得到了一个全新的数据记录:
| ID | 商品种类 |
|---|---|
| T1 | a,b,c |
| T2 | a,c |
| T3 | b,c |
看到这个类似的表,是不是很熟悉,我们需要根据现在这个新的数据记录表,开始构建一个新的FpTree,方法依旧和上文一样,这里只给出新的FpTree的结构:

这个新的FpTree已经建立好了,只要这个新的FpTree的路径不是1条,那我们就继续递归的挖掘。
如果新的FpTree的路径恰好就1条,那么这条路径上所有节点的组合就是条件频繁项集,假设 d 节点的条件频繁项集是 x,y,z ,那么a的频繁项集就是 (x,d),(y,d),(z,d),可以看到这里的每个项集都有a这个后缀,因为您本来就是依据d节点建立的新数据集,求出这个新的数据集的条件频繁项集后,要求出原来的数据集的频繁项集,就要在这个条件频繁项集的后面加上 d节点。
回到这个具体的例子,可以看到新的数据记录构建的FpTree,只有一条路径,那么递归结束,这条路径有两个节点(null,c),一定不要忘记null节点,null就是表示一个空节点。
两个节点的所有组合就是条件频繁项集,即{ null,c },有一点需要注意,(null,c)和(c)是一样的,这两个没有区别。那么,最后,d的频繁项集就是{ (d),(c,d) }。
- 接下来看表头的倒数第二个项,即 c 节点,根据构建的线索,找出所有的c节点,节点所在的所有分支为 {(a,b,c :2),(a,c :1),(b,c :1)},(提示:后面的数字是c节点的count值,数字 ”2“ 代表这条分支出现了2次),同样的,去除掉c节点,(去除c节点时,c节点后面的节点同样也被去掉了),故可得新是数据集{(a,b :2),(a :1),(b :1)},做个表格,如下:
| ID | 商品种类 |
|---|---|
| T1 | a,b |
| T2 | a,b |
| T3 | a |
| T4 | b |
a,b这个组合在表格中出现了2次,因为它在分支中出现了2次,(在这里,我之所以把它重复2次的写入数据记录表中,其实是为了能复用我们之前的代码,这样就不用重新在写一个函数了。在实际的数据情况中,如果a,b组合出现了1000次,我如果把它展开到数据记录中,这个数据记录就有1000行相同信息的记录了,这样显然不合适,我们需要在编写一个函数,在构建FpTree时,直接把这条数据的count设为1000即可,这样会大大节省时间)
对上面这个新的表构建FpTree,结构如下图:

它同样是一条单一路径,路径上节点的所有组合即为条件频繁项集,别忘了空节点null,条件频繁项集为(null),(a),(b),(a,b), 那么c的频繁项集就是 { (c),(a,c),(b,c),(a,b,c) }。
显然,这一组的频繁项集始终有一个相同的后缀 c,因此这一组的频繁项集永远不会和上一组重复。
- 在看倒数第3个节点,b节点,处理方式和前两个一样,留给读者做练习,这里直接给出该节点的频繁模式树FpTree:

4. 最后一个节点,a节点,它的条件频繁项集是 { null },频繁项集就是{ (a) }。
- 至此,整个算法流程已经叙述完了,补充一点,在不断递归求新的数据记录,建立的新的FpTree时,只要新的FpTree路径不是1条,就可以继续递归,直到新的FpTree路径为1时,结束递归,进行处理。当然也可以用迭代,只不过代码会显的一点多,不如递归清晰。
代码实现
FpGrowthClass.py
这颗树的节点结构,用python类的表示:
'''
Frequent Pattern Tree 繁模式树
牛奶 a 面包 b 尿布 c 啤酒 d 可乐 e 鸡蛋 f
所用数据集
T1 {牛奶,面包}
T2 {面包,尿布,啤酒,鸡蛋}
T3 {牛奶,尿布,啤酒,可乐}
T4 {面包,牛奶,尿布,啤酒}
T5 {面包,牛奶,尿布,可乐}
转化为字母表示,即
数据集
database = [ ['a', 'b'],
['b', 'c', 'd', 'f'],
['a', 'c', 'd', 'e'],
['b', 'a', 'c', 'd'],
['b', 'a', 'c', 'e'] ]
'''
class FpNode():
def __init__(self, name='', childs={}, parent={}, nextCommonId={}, idCount=0):
self.idName = name # 名字
self.childs = childs # 所有孩子结点
self.parent = parent # 父节点
self.nextCommonId = nextCommonId # 下一个相同的 id名字 结点
self.idCount = idCount # id 计数
def getName(self): #获取该节点名字
return self.idName
def getAllChildsName(self): #获取该节点所有孩子节点的名字
ch = self.childs
keys = list(ch.keys())
names = []
for i in keys:
names.append( list(i))
return names
def printAllInfo(self): #打印该节点所有信息
print(self.idName, self.idCount, list(self.childs.keys()), list(self.parent.keys()), self.nextCommonId.items() )
@classmethod
def checkFirstTree(cls, rootNode): #前序遍历整个树(这不是二叉树,没有中序遍历)
if rootNode is None:
return ''
#parent1 = rootNode.parent.keys() #要加一个 强转 ,否则它会变成 Nopetype 型,
rootNode.printAllInfo() # print(rootNode.idName, type(rootNode.parent)) 报错 root <class 'NoneType'>
if rootNode.childs is not None:
keys = list(rootNode.childs.keys())
for i in keys:
cls.checkFirstTree(rootNode.childs[i])
@classmethod
def checkBehindTree(cls, rootNode): #后序遍历整个树
if rootNode is None:
return ''
if rootNode.childs is not None:
keys = list(rootNode.childs.keys())
for i in keys:
cls.checkBehindTree(rootNode.childs[i])
rootNode.printAllInfo()
main.py
主函数及算法实现:(请从最后的main函数开始看起)
from practice04_FpGrowth.FpNodeClass import FpNode
import copy
def scan1_getCand1(database): #第一次扫描统计出现的次数
c1 = {} #候选集
for i in database:
for j in i:
c1[j] = c1.get(j, 0) + 1 #表示如果字典里面没有想要的关键词,就返回0
#print(c1)
return c1
#返回排好序的字典
#对数据进行排序,按支持度由大到小排列
def sortData(**d): #形参前添加两个 '*'——字典形式 形参前添加一个 '*'——元组形式
sortKey = list(d.keys()) #直接使用sorted(my_dict.keys())就能按key值对字典排序
sortValue = list(d.values())
length = len(sortKey)
for i in range(length-1): #按照支持度大小,由大到小排序的算法
for j in (i, length-1-1): #必须 -1 (1,len)虽然不包含 len本身 但是数组【len-1】时最后一个元素,必须减去这个元素
if sortValue[i] < sortValue[j + 1]:
sortValue[i], sortValue[j + 1] = sortValue[j + 1], sortValue[i] #如果它的支持度小与另一个,交换位置
sortKey[i], sortKey[j + 1] = sortKey[j + 1], sortKey[i]
new_c1 = {} #存放排完序的数据记录
for i in range(length):
new_c1[sortKey[i]] = sortValue[i]
return new_c1 #返回排好序的字典
#得到 database 的频繁项集
def getFreq(database, minSup = 3, **c1): #返回频繁项集,和频繁项集的支持度
c1 = scan1_getCand1(database) #第一次扫面数据库,求第一次候选集,返回的是字典
new_c1 = sortData(**c1) #排序,大到小
keys = list(new_c1.keys())
for i in keys:
if new_c1[i] < minSup: #若支持度小于最小支持度,则删除该商品
del new_c1[i]
f1 = [] # 第一次频繁项集
new_keys = list(new_c1.keys())
for i in new_keys:
if [i] not in f1:
f1.append( [i] ) #每个元素自成一项
#print(f1,new_c1)
return f1, new_c1
def createRootNode(): #创建一个根节点
rootNode = FpNode('root', {}, {}, {}, -1) #name, childs, parent, nextCommonId, idCount
return rootNode
def buildTree(database, rootNode, f1): #构建频繁模式树 FpTree
for i in database: #第二次扫描数据库
present = rootNode #指向当前节点
next = FpNode(name='', childs={}, parent={}, nextCommonId={}, idCount=0) #创建一个新节点,并初始化
for j in f1: #按支持度从大到小的顺序进行构建节点
if set(j).issubset(set(i)): #j如果在i里面
if (present.getName() is 'root') and j not in rootNode.getAllChildsName():
next.idName = str(j[0]) #对新创建的节点进行赋值
next.idCount = next.idCount + 1
next.nextCommonId = {str(j[0]): 0}
next.parent.update({rootNode.idName:rootNode})
temp = copy.copy(next)
rootNode.childs.update({str(j[0]):temp}) #往它插入父亲节点
##print(temp.parent)
present = temp #present = next 这样直接赋值是 引用 ,一定要注意
next = FpNode(name='', childs={}, parent={}, nextCommonId={}, idCount=0) #创建并初始化下一个新节点
else:
if j in present.getAllChildsName(): #如果需要插入的节点已经存在
temp2 = present.childs[str(j[0])]
present = temp2
present.idCount = present.idCount + 1 #count+1即可
else:
next.idName = str(j[0]) #对新插入的节点赋值
next.idCount = next.idCount + 1
next.nextCommonId = {str(j[0]): 0}
next.parent.update({present.idName:present})
#temp3 = copy.copy(next)
present.childs.update({str(j[0]):next}) #往它插入父亲节点
#temp3.childs = {}
present = next
next = FpNode(name='', childs={}, parent={}, nextCommonId={}, idCount=0)
#present = next
#next = FpNode()
#print(rootNode.getAllChildsName())
# print('前序遍历如下:')
# FpNode.checkFirstTree(rootNode)
# print('后序遍历如下:')
# FpNode.checkBehindTree(rootNode)
return None
#构建线索,填节点的nextCommonId这个属性
def buildIndex(rootNode, d1): #传 列表或字典时,列表前,加*, 字典前加 ** 表示传给函数的是一个地址,在函数内部改变这个参数,不会影响到函数外的变量
if rootNode is None:
return ''
next = rootNode #指向下一个节点,当前赋值为根节点
value = rootNode.idName
#print(value)
#print(d1[str(value)]) #d1[value] {KeyError}'a'??????????????? 如果value是根节点root,就会出错,表中本来就没有root这个值
#print(d1)
if value != 'root':
indexAds1 = {value: d1[value]}
if d1[value] == 0: # 线索构造 我已经把初始化了所有的 nextCommonId 为 {'': 0}
# 所以后面只要 这个节点的 nextCommonId字典的值为0,就说明这个字典就是构建的链表链尾
d1[value] = next
# print(indexAds1)
else:
while indexAds1[value] != 0:
indexAds1 = indexAds1[value].nextCommonId #以链表形式把最后一个 表尾元素找出来
#print(indexAds1)
indexAds1[value] = next #这个元素后面加入 当前所在树的这个节点的地址
#print(next.nextCommonId)
if rootNode.childs is not None: #根节点孩子不是null,则对它的每个孩子,依次递归进行线索构建
keys = list(rootNode.childs.keys())
for i in keys:
buildIndex(rootNode.childs[i], d1)
def createIndexTableHead(**indexTableHead): #创建一个表头,用来构建线索,表头的名字是相应节点的名字
keys = list(indexTableHead.keys())
#print(keys)
for i in keys:
indexTableHead[i] = 0
return indexTableHead
def getNewRecord(idK, **indexTableHead): #得到新的数据记录
newData = []
address = indexTableHead[idK]
while address != 0:
times = 0
times = address.idCount #当前节点count数
l = [] #临时存放这个分支上的所有节点元素,单个单个存储 二维列表
getOneNewR = [] #和l一样,是l的倒叙,因为l本来是倒叙的,现在把它改成倒叙
#print(list(address.parent.keys())[0]) #这样写才是 字符 c 而不是 'c'
nextAdress = copy.copy(address)#一个指针,指向父亲节点,初始化为表头第一个的地址
while list(nextAdress.parent.keys())[0] is not 'root': #该节点发父亲节点不是根节点。则
#print(address.parent)
l.append(list(nextAdress.parent.keys())) #把它的父亲节点加入l中
parentIdName = list(nextAdress.parent.keys())[0] #父亲节的名字
nextAdress = nextAdress.parent[ parentIdName ] #指向该节点父亲节点
if l != []:
for j in l:
getOneNewR.append(j[0])
if getOneNewR != []:
for k in range(times): #若最后的那个 idk 计数为多次,要把它多次添加到新产生的newData中
newData.append(list(getOneNewR))
#把得到的记录加入新的数据集中
address = address.nextCommonId[idK] #指向下一个表头元素的开始地址,进行循环
return newData
# idK表示当前新产生的数据集是在去除这个字母后形成的, fk是去除掉idk后,新的第一次频繁项集 dk是fk的支持度
def getAllConditionBase(newDatabase,idK, fk, minSup, **dk): #返回条件频繁项集 base, 和支持度
if fk != []: #频繁项集非空
newRootNode = createRootNode() #创建新的头节点
buildTree(newDatabase, newRootNode, fk)
#newIndexTableHead = {} #创建新表头
newIndexTableHead = createIndexTableHead(**dk) # **dk 就是传了个值,给了它一个拷贝,修改函数里面的这个拷贝,不会影响到外面的这个变量的值
buildIndex(newRootNode, newIndexTableHead)
else:
return [idK], {idK:9999} #频繁项集是空的,则返回idk的名字,支持度设为最大值9999,这样会出现一些问题,最后已经解决了,在主函数代码中有表现出来
if len(newRootNode.getAllChildsName()) < 2: #新的FpTree只有1条分支,(这里只认为根节点只有1个孩子,就说他只有一条分支)
#若是实际数据,就不能这样写了,应当在写一个函数,从根节点开始遍历,确保每个节点都只有1个孩子,才能认为只有1条分支
base = [[]] #条件基
node = newRootNode
while node.getAllChildsName() != []: #当前节点有孩子节点
childName = list(node.childs.keys()) #一个列表,孩子节点的所有名字,其实就1个孩子,前面已经判断了是单节点
base.append(list(childName[0])) # 把孩子节点加入条件基
#print(node.childs)
#print(childName)
node = node.childs[childName[0]] #指向下一个节点
#print(base)
itemSup = {node.idName : node.idCount} #这一条分支出现的次数,最后求频繁项集支持度需要用到
#print(itemSup)
return base, itemSup #返回条件基,还有这一条分支出现的次数,
else: #分支不止1条,进行递归查找,重复最开始的操作
base = [[]]
for commonId in fk[-1::-1]: #倒叙进行
newIdK = str(commonId[0])
newDataK = getNewRecord(newIdK, **newIndexTableHead) # 传入这个表头的一个拷贝
fk2, dk2 = getFreq(newDataK, minSup)
conditionBase, itemSup = getAllConditionBase(newDataK, newIdK, fk2, minSup, **dk2) #得到该条件基下的条件基,及各个分支出现次数
#递归进行
base.append(conditionBase)
return base, itemSup
#FpGrowth算法本身(Frequent Pattern Growth—-频繁模式增长)
def FpGrowth(database, minSup = 3):
f1, d1 = getFreq(database, minSup) #求第一次频繁项集,并返回一个字典存放支持度,且按大到小排序,返回频繁项和存放频繁项支持度的字典
rootNode = createRootNode() #创建根节点
#print(f1,d1) #[['a'], ['b'], ['c'], ['d']] {'a': 4, 'b': 4, 'c': 4, 'd': 3}
# 第一步建造树
buildTree(database,rootNode, f1)
#indexTableHead = {} #创建线索的表头,一个链表
indexTableHead = createIndexTableHead(**d1) # **d1 就是传了个值,给了它一个拷贝,修改函数里面的这个拷贝,不会影响到外面的这个变量的值
buildIndex(rootNode, indexTableHead) #创建线索,用这个表头
# print('构建线索后,前序遍历如下:')
# FpNode.checkFirstTree(rootNode)
# print('构建线索后,后序遍历如下:')
# FpNode.checkBehindTree(rootNode)
freAll = [] #所有频繁项集
freAllDic = {} #所有频繁项集的支持度
#第二步 进行频繁项集的挖掘,从表头header的最后一项开始。
for commonId in f1[-1::-1]: #倒叙 从支持度小的到支持度大的,进行挖掘
idK = str(commonId[0])
newDataK = getNewRecord(idK, **indexTableHead) #传入这个表头的一个拷贝, 函数返回挖掘出来的新记录
fk, dk = getFreq(newDataK, minSup) #对新数据集求频繁项集
#print(fk,dk)
base, itemSup= getAllConditionBase(newDataK, idK, fk, minSup, **dk) #得到当前节点的条件频繁模式集,返回
#有可能会发生这样一种情况,条件基是 a ,然后fk,dk为空,结果这个函数又返回了 a,那么最后的结果中,就会出现 a,a 这种情况,处理方法请往下看
#print(base,idK)
for i in base:
#print(i)
t = list(i)
t.append(idK)
t = set(t) #为了防止出现 重复 的情况,因为我的getAllConditionBase(newDataK, idK, fk, minSup, **dk)方法的编写,可能会形成重复,如 a,a
t = list(t)
freAll.append(t)
itemSupValue = list(itemSup.values())[0]
x = tuple(t) #列表不能做字典的关键字,因为他可变,,而元组可以
#<class 'list'>: ['c', 'd']
#print(t[0]) # t是列表,字典的关键字不能是可变的列表, 所以用 t[0] 来取出里面的值
freAllDic[x] = min(itemSupValue, d1[idK])
#print(freAll)
#print(freAllDic)
return freAll, freAllDic
if __name__ == '__main__':
database = [['a', 'b'],
['b', 'c', 'd', 'f'],
['a', 'c', 'd', 'e'],
['b', 'a', 'c', 'd'],
['b', 'a', 'c', 'e']]
freAll, freAllDic = FpGrowth(database, minSup = 3)
# minSup = 3 [['d'], ['d', 'c'], ['c'], ['c', 'a'], ['c', 'b'], ['b'], ['b', 'a'], ['a']]
print(freAll)
print("各个频繁项集的支持度依次为:")
for i in freAllDic.keys():
print(i, freAllDic[i])

算法优缺点分析
优点:
- 只需扫描数据库两次,大大减少I/O操作
- 不产生候选项集,效率高于Apriori
- 采用分治策略,适合处理大规模数据集
- 通过FpTree压缩存储,节省内存空间
缺点:
- FpTree构建需要内存足够存放压缩后的数据
- 递归挖掘可能消耗较多内存
- 实现比Apriori复杂,尤其是链表维护部分
总结
对比与适用场景
| 对比维度 | Apriori算法 | FpGrowth算法 |
|---|---|---|
| 扫描次数 | 多次扫描(每次迭代) | 仅需2次扫描 |
| 候选项集 | 产生大量候选项集 | 不产生候选项集 |
| 时间复杂度 | O(2^n) | O(n²) |
| 空间复杂度 | 较低 | 较高(需存储FpTree) |
| 实现难度 | 简单 | 较复杂 |
| 适用场景 | 小规模数据集,最小支持度高 | 大规模数据集,最小支持度低 |
实际应用建议
- 数据预处理:无论使用哪种算法,都需要对数据进行适当的预处理,包括数据清洗、离散化等。
- 参数调优:最小支持度和最小置信度的设置对结果影响很大,需要根据具体业务场景进行调整。
- 结果解释:挖掘出的关联规则需要结合业务知识进行解释和验证,避免出现无意义的规则。
- 算法选择:
- 对于初学者或小规模数据,建议从Apriori开始
- 对于大规模数据或性能要求高的场景,应选择FpGrowth
- 也可以考虑其他改进算法如Eclat、HMine等
- 性能优化:
- 对于Apriori,可以通过事务压缩、划分等方法优化
- 对于FpGrowth,可以考虑并行化或分布式实现
随着大数据技术的发展,关联规则挖掘算法也在不断演进,出现了许多基于MapReduce、Spark的并行化实现,以及处理流数据、不确定数据等新型数据的改进算法。掌握这些经典算法的原理和实现,是理解和应用更高级算法的基础。























 1890
1890

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








