2.3 高阶导数

 

---

 思维导图：

---

学习目标：

我学习高阶导数，我会按照以下步骤进行：

1. 复习一阶导数的概念和计算方法。高阶导数是指对函数进行多次求导，因此首先需要熟悉一阶导数的概念和求导公式，例如常见函数的导数规律、链式法则、反函数求导等。(复习很重要，给知识划分不同房间，记住提取时的基本信息即钥匙)
2. 了解高阶导数的概念和计算方法。高阶导数指对一阶导数进行求导得到的导数，例如二阶导数表示对原函数的一阶导数再求导。要熟悉高阶导数的概念和求导公式，例如二阶导数的定义和计算方法、高阶导数的通式等。
3. 熟悉高阶导数的性质和应用。高阶导数具有许多重要的性质，例如连续性、凹凸性、拐点、最值等，这些性质对于函数的研究和应用非常重要。要学会应用高阶导数来研究函数的性质，例如判断函数的最值、拐点等。
4. 刷题巩固。通过练习题目，加深对高阶导数的理解，掌握其求导技巧和应用方法。要注意各种题型的特点和难点，例如多次求导的计算和简化、高阶导数的应用、函数性质的证明等。
5. 反复温习和总结。学习高阶导数需要反复温习和总结，加深理解，强化记忆，避免遗忘。同时要及时总结和归纳高阶导数的知识点，形成体系化的学习框架，有助于加深对知识点的理解和应用。

 

 

 

 

 

 

 

 

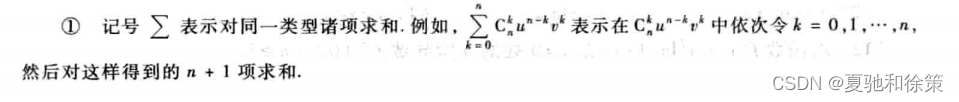
 总结：

高阶导数是微积分中一个重要的概念，其定义是对原函数反复求导得到的导函数。以下是高阶导数的重点、难点以及易错点注意事项的总结：

• 重点：
• 高阶导数的定义：高阶导数指对原函数进行多次求导得到的导函数，可以用记号f^(n)(x)来表示。
• 高阶导数的求法：可以使用基本的求导公式，或者利用Leibniz公式来求解高阶导数。
• 高阶导数的意义：高阶导数描述了原函数的曲率和弯曲程度，在物理学、工程学、经济学等领域中有广泛的应用。
• 难点：
• Leibniz公式的应用：Leibniz公式是计算高阶导数的重要方法，但其使用较为繁琐，需要掌握一定的技巧。
• 高阶导数的符号：高阶导数的符号可能会比较复杂，需要根据求导的次数来确定符号。
• 高阶导数的性质：高阶导数的性质与一阶导数的性质有所不同，需要特别注意。
• 易错点及注意事项：
• 符号错误：求导过程中可能会出现符号错误，需要注意符号的正确性。
• 求导次数错误：在求高阶导数时，容易出现求导次数错误的情况，需要注意。
• 计算错误：高阶导数的计算过程比较复杂，容易出现计算错误，需要注意计算的准确性。
• 应用场景的理解：高阶导数在不同领域中的应用有所差异，需要理解其应用场景。
• 总之，掌握高阶导数的求法、意义、性质以及应用，能够更深入地理解微积分的概念和方法，有助于进一步研究微积分的高级内容，对于数学、物理、工程等领域都有重要的意义。在学习过程中，需要注意以上难点和易错点，加强练习，提高自己的运用能力。