5-2 运算及其性质

思维导图：

 

 

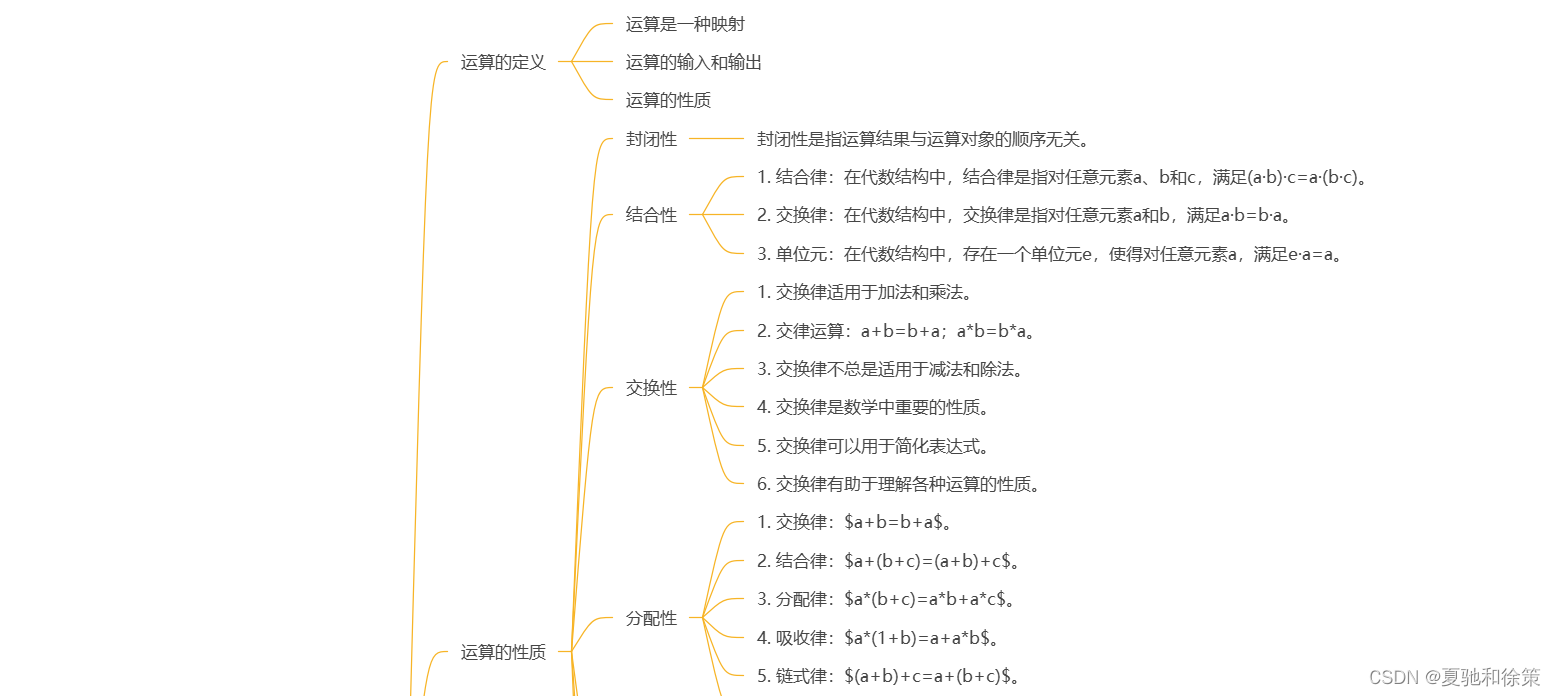
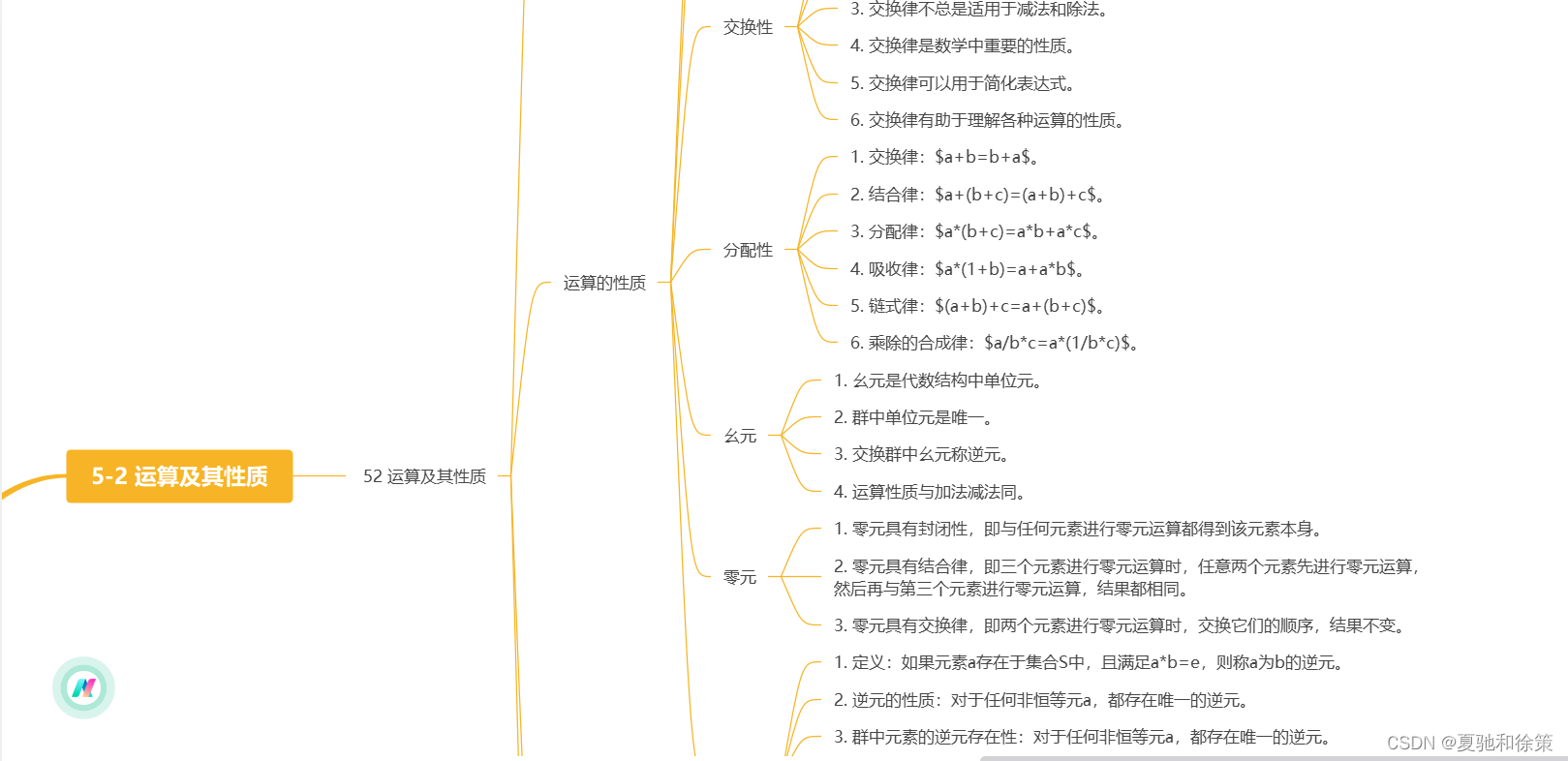
5-2 运算及其性质

1. 二元运算的基本性质

• 封闭性 (定义5-2.1)

  • 如果对于任意的 x,y∈A，都有 x∗y∈A，则称运算 ∗A 上是封闭的。
  • 例题1: 集合 A={x∣x=2n,n∈N}，乘法封闭，加法不封闭。

• 可交换性 (定义5-2.2)

  • 如果对于任意的 x,y∈A，都有 ∗y=y∗x，则称该运算 ∗∗ 是可交换的。
  • 例题2: 有理数集 Q 上的运算 ΔΔ，可交换。

• 可结合性 (定义5-2.3)

  • 如果对于任意的 x,y,z∈A，都有 (x∗y)∗z=x∗(y∗z)，则称该运算是可结合的。
  • 例题3: 集合 A 上的运算 ⋆⋆，可结合。

• 分配律 (定义5-2.4)

  • 如果对于任意的 x,y,z∈A，都有 x∗(yΔz)=(x∗y)Δ(x∗z) 和 (yΔz)∗x=(y∗x)Δ(z∗x)，则称运算 ∗∗ 对于运算 ΔΔ 是可分配的。
  • 例题4: 集合 A={a,β}，运算 ΔΔ 对于运算 ∗∗ 可分配。

• 吸收律 (定义5-2.5)

  • 如果对于任意的 x,y∈A，都有 x∗(xΔy)=x 和xΔ(x∗y)=x，则称运算 ∗∗ 和运算 ΔΔ 满足吸收律。
  • 例题5: 自然数集 N，运算 ∗∗ 和 ⋆⋆ 满足吸收律。

2. 特殊元素的性质

• 等幂律 (定义5-2.6)

  • 如果对于任意的 x∈A，都有 x∗x=x，则称运算 ∗∗ 是等幂的。
  • 例题6: 集合的幂集上的并、交运算满足等幂律。

• 幺元和零元 (定义5-2.7, 5-2.8)

  • 幺元：如果有元素 e，使得对于任意的 x，有 e∗x=x∗e=x。
  • 零元：如果有元素 00，使得对于任意的 x，有 ∗0=00∗x=x∗0=0。
  • 例题7: 集合 S，运算 ∗∗ 和 ⋆⋆ 的幺元和零元。

3. 运算表分析

• 运算表特性
  • 封闭性：运算表中每个元素都属于 A。
  • 可交换性：运算表关于主对角线对称。
  • 等幂性：主对角线元素与其行（列）表头元素相同。
  • 零元：对应元素的行和列中所有元素与该元素相同。
  • 幺元：对应元素的行和列与运算表行列一致。
  • 逆元：位于对应行列的元素是幺元。

 

定义： 

定义 5-2.1（封闭二元运算）：

• 二元运算：在集合 A 上定义的操作，涉及两个元素的运算，记作 ∗∗。
• 封闭性：如果对于任意的 x,y∈A，都有 x∗y∈A，则称运算 ∗∗ 在集合 A 上是封闭的。

解释：

• "二元"的含义：二元运算意味着运算涉及两个输入元素。例如，加法 ++ 和乘法 ×× 都是二元运算，因为它们需要两个数来进行计算。
• 封闭性：封闭性是指运算的结果仍然属于原始集合。例如，如果集合 A 是所有整数的集合，那么整数的加法和乘法都是封闭的，因为任意两个整数的和或积仍然是一个整数。
• 重要性：封闭性是数学结构（如群、环、域）定义的重要部分。一个运算如果不是封闭的，那么它可能导致一些运算结果跳出原始集合的范围。

应用实例：

1. 整数加法：在整数集合 Z 上，加法 ++ 是封闭的，因为任意两个整数相加仍然是整数。
2. 实数乘法：在实数集合 R 上，乘法 ×× 是封闭的，因为任意两个实数相乘的结果仍是实数。
3. 非封闭例子：如果集合 A 是所有正整数的集合，那么减法就不是封闭的，因为正整数相减可能得到负数或零，而这些不属于集合 A。

封闭性是理解更复杂的代数结构的基础，也是数学中构建严密和一致性系统的关键部分。

定义 5-2.2（可交换二元运算）：

• 二元运算：在集合 A 上定义的操作，涉及两个元素的运算，记作 ∗∗。
• 可交换性：如果对于任意的 x,y∈A，都有 x∗y=y∗x，则称运算 ∗∗ 在集合 A 上是可交换的。

解释：

• "二元"的含义：二元运算意味着运算涉及两个输入元素。例如，加法和乘法都是二元运算，因为它们需要两个数来进行计算。
• 可交换性：这个性质指出，运算的顺序不影响结果。换句话说，改变操作数的顺序不会改变运算的结果。
• 重要性：可交换性是许多数学结构（如群、环、域）的关键属性之一。它在简化数学运算和理论证明中扮演着重要角色。

应用实例：

1. 整数加法：在整数集合 Z 上，加法是可交换的，因为对于任何两个整数 a 和 b，有 a+b=b+a。
2. 实数乘法：在实数集合 R 上，乘法是可交换的，因为任意两个实数的乘积与它们的乘积顺序无关。
3. 非可交换例子：矩阵乘法就不是可交换的，因为矩阵的乘积通常依赖于乘法的顺序。

可交换性是代数系统和更广泛的数学概念中的一个基础属性，对于理解和操作代数结构至关重要。

定义 5-2.3（结合二元运算）：

• 二元运算：在集合 A 上定义的操作，涉及两个元素的运算，记作 ∗∗。
• 结合性：如果对于任意的 x,y,z∈A，都有 (x∗y)∗z=x∗(y∗z)，则称运算 ∗∗ 在集合 A 上是结合的。

解释：

• "二元"的含义：二元运算意味着运算涉及两个输入元素，例如加法、乘法或其他任何两个输入的操作。
• 结合性的重要性：结合性意味着在进行连续的运算时，运算的组合顺序不影响最终结果。
• 应用：结合性在代数系统的定义中非常重要，特别是在群、环和域等结构中。

应用实例：

1. 整数加法：在整数集合 Z 上，加法是结合的，因为对于任何三个整数 a,b, 和 c，都有 (a+b)+c=a+(b+c)。
2. 实数乘法：在实数集合 R 上，乘法是结合的，因为任意三个实数的乘积与它们的组合顺序无关。

非结合性例子：

• 减法通常不是结合的。例如，在整数集合中，(5−3)−2≠5−(3−2)(5−3)−2=5−(3−2)。

结合性是理解和操作代数结构的关键概念，它保证了运算的一致性和可预测性，特别是在执行多步运算时。这个定义提供了对二元运算结合性的清晰理解，是构建更复杂代数系统的基础。

定义 5-2.4（分配律）：

• 二元运算：在集合 A 上定义的两个操作，分别记作 ∗∗ 和 △△。
• 分配律：如果对于任意的 x,y,z∈A，都有以下两个等式成立：
  1. x∗(y△z)=(x∗y)△(x∗z)
  2. (y△z)∗x=(y∗x)△(z∗x) 那么称运算 ∗∗ 对于运算 △△ 是可分配的。

解释：

• 分配性的含义：在这个定义中，分配性意味着当你将一个运算（如 ∗∗）应用于另一个运算（如 △△）的结果时，你可以独立地将第一个运算应用于第二个运算的每个操作数，然后再应用第二个运算。
• 重要性：分配律是许多代数结构（尤其是环和域）的基本属性之一。它确保了不同运算之间的一致性和协调。

应用实例：

1. 整数加法和乘法：在整数集合 Z 上，乘法 ∗∗ 对加法 ++ 是可分配的，即 =(�×�)+a×(b+c)=(a×b)+(a×c)。
2. 实数加法和乘法：在实数集合 R 上，乘法对加法也是可分配的。

非分配性例子：

• 有些运算可能不满足分配律。例如，减法通常不对加法满足分配律。

分配律是理解更复杂的代数结构和操作的关键概念，它在形成一致的代数系统和进行代数证明中起着至关重要的作用。这个定义提供了对于如何在代数系统中处理和理解多种运算的清晰框架。

定义 5-2.5（吸收律）：

• 二元运算：在集合 A 上定义的两个可交换二元运算，分别记作 ∗∗ 和 △△。
• 吸收律：如果对于任意的 x,y∈A，都满足以下两个等式：
  1. x∗(x△y)=x
  2. △(x∗y)=x 那么称运算 ∗∗ 和运算 △△ 满足吸收律。

解释：

• 吸收律的含义：吸收律表明，在一对运算中，一个元素与另一个运算的结果进行运算时，可以“吸收”其中的一个元素，从而简化为原始元素本身。
• 应用与重要性：吸收律在某些代数结构，如格（Lattices）和布尔代数中非常重要。它有助于简化表达式并在逻辑运算和集合理论中发挥重要作用。

应用实例：

1. 逻辑运算：在布尔代数中，逻辑与（AND）和逻辑或（OR）运算满足吸收律。例如，对于任意布尔值 x 和 y，都有 AND ( OR )=x AND (x OR y)=x。
2. 集合运算：在集合论中，交集和并集运算满足吸收律。例如，对于任意集合 X 和 Y，都有 X∩(X∪Y)=X。

吸收律是理解和操作复杂代数结构的基础，尤其是在涉及更复杂的逻辑结构和集合操作时。这个定义提供了对于运算间相互作用的基本理解，是构建严密代数系统的关键部分。

定义 5-2.6（等幂性）：

• 二元运算：在集合 A 上定义的操作，涉及两个元素的运算，记作 ∗∗。
• 等幂性：如果对于任意的 x∈A，都有 ∗x=x，则称运算 ∗∗ 在集合 A 上是等幂的。

解释：

• 等幂运算的含义：等幂性意味着当一个元素与自身进行某种二元运算时，结果仍然是该元素本身。
• 重要性：等幂性在某些代数结构中非常重要，如布尔代数、某些类型的格（lattices）和环结构。它有助于简化运算和公式。

应用实例：

1. 逻辑运算：在布尔代数中，逻辑与（AND）和逻辑或（OR）运算是等幂的。例如， AND x AND x=x 和  OR  OR x=x。
2. 集合运算：在集合论中，集合的并集和交集运算是等幂的。例如，对于任意集合 X，都有 X∪X=X 和 X∩X=X。

等幂性是一个简单但强大的概念，它在简化表达式和证明中扮演着重要角色。这个定义为理解和应用代数结构中的二元运算提供了基础。

定义 5-2.7（幺元）：

• 二元运算：在集合 A 上定义的操作，涉及两个元素的运算，记作 ∗∗。
• 左幺元：如果存在一个元素 e∈A 使得对于所有 x∈A，有 e∗x=x，则称 e 为关于运算 ∗∗ 的左幺元。
• 右幺元：如果存在一个元素 e′∈A 使得对于所有 x∈A，有 x∗e′=x，则称 ′e′ 为关于运算 ∗∗ 的右幺元。
• 幺元：如果一个元素 e 同时是左幺元和右幺元，即对所有 x∈A，都有 e∗x=x∗e=x，则称 �e 为关于运算 ∗∗ 的幺元。

解释：

• 幺元的重要性：幺元在代数结构中扮演着基本的角色，特别是在群、环、域等结构中。它类似于数字 1 在乘法运算中的角色，作为一种“不改变其他元素”的特殊元素。
• 左幺元和右幺元的区别：在某些代数结构中，左幺元和右幺元可能不相同，但在群、环和域等结构中，它们通常是相同的。

应用实例：

1. 整数加法：加法运算 ++ 的幺元是 0，因为对于任何整数 a，都有 0+a=a+0=a。
2. 实数乘法：乘法运算 ×× 的幺元是 1，因为对于任何实数 a，都有 1×a=a×1=a。

易错点：

• 在一些非交换的代数结构中（如某些类型的矩阵），左幺元和右幺元可能不相同。

幺元的概念是代数系统理论的一个关键部分，有助于理解如何构造和操作复杂的数学结构。这个定义为理解代数系统中的基本运算和元素关系提供了重要的基础。

 定理证明：

定理 5-2.1（幺元的唯一性）：

在集合 A 上定义的二元运算 ∗∗，如果存在左幺元 e1​ 和右幺元 e2​，则 e1​=e2​，且 A 中的幺元是唯一的。

证明过程：

1. 证明左幺元和右幺元相等：

   • 因为 e1​ 是左幺元，对于所有 x∈A，有 e1​∗x=x。
   • 因为 e2​ 是右幺元，对于所有 x∈A，有 2=x∗e2​=x。
   • 将 x 替换为 e2​ 并应用这两个性质，得到 e1​∗e2​=e2​。
   • 将 x 替换为 e1​ 并应用这两个性质，得到 e1​∗e2​=e1​。
   • 由上述两点，可得 e1​=e2​。

2. 证明幺元的唯一性：

   • 设 ′e′ 是 A 中的另一个幺元。
   • 由幺元的定义，对于所有 x∈A，有 e′∗x=x 和 x∗e′=x。
   • 将 x 替换为 e（上一步证明的唯一幺元），得到 e′∗e=e 和 e∗e′=e。
   • 由 e′∗e=e 和 2e=e1​=e2​，得到 e′=e。
   • 因此，幺元 ′e′ 必须等于 e，证明了幺元的唯一性。

结论：

定理 5-2.1 证明了如果一个代数结构中存在左幺元和右幺元，那么这两个元素实际上是相同的，即存在唯一的幺元。这个证明过程显示了逻辑推理在证明数学属性中的重要性，并阐明了代数结构中幺元的基本特性。

 总结：

学到了什么？

1. 逻辑推理的重要性：证明展示了如何使用逻辑推理从已知的假设（左幺元和右幺元的存在）推导出结论（幺元的唯一性）。这种推理技巧在数学和其他领域的问题解决中都非常重要。

2. 代数结构的理解：证明深化了对代数结构（如群、环、域）中幺元概念的理解。了解如何一个元素能作为操作的单位元素，且其唯一性如何被保证，对于深入理解这些结构至关重要。

3. 运算性质的重要性：证明强调了二元运算性质（如封闭性、结合性）在确定结构的特性（如幺元的唯一性）中的作用。

4. 代数系统的性质：通过理解幺元的概念及其在代数系统中的角色，我们可以更好地理解和操作更复杂的代数系统。

5. 数学定义的实际应用：证明示例了如何将数学定义（左幺元和右幺元）应用于具体情境中，展现了定义在构建数学论证中的重要性。

6. 数学概念的普遍性：幺元的概念在不同的数学领域中广泛存在，了解其基本性质有助于在更广泛的背景下应用这些概念。

7. 证明方法的示范：这个证明是一个很好的示范，显示了如何将简单的数学原理和逻辑应用于证明更复杂的数学命题。

总之，这个证明不仅提供了关于幺元的具体知识，还展示了数学推理和证明方法的基本框架，这些对于解决更复杂的数学问题非常有帮助。

数学思想

1. 结构的重要性：数学结构（如代数系统中的集合和运算）的理解对于深入学习数学至关重要。
2. 元素的特性：每个数学元素（如幺元）在其结构中扮演特定的角色，理解这些角色有助于理解整个结构。
3. 普遍性与特殊性：数学概念通常具有普遍性，但在特定条件下展现出独特的性质。

数学思维

1. 逻辑推理：逐步分析，从已知条件出发，逻辑地推导出结论。
2. 从特殊到一般：通过特定实例（如左幺元和右幺元）理解一般概念（如幺元的唯一性）。
3. 条件的应用：明确条件（如运算的定义和性质）如何影响结论。

数学证明方法

1. 直接证明：从已知事实出发，直接推导出需要证明的命题。
2. 使用定义：充分利用数学定义来构建证明的基础。
3. 等价转换：通过等价的数学表达式或操作简化问题。

数学证明处理技巧

1. 分步处理：将复杂问题分解为更简单的步骤。
2. 应用性质：利用已知的数学性质（如封闭性、等幂性）来简化问题或证明。
3. 寻找连接：寻找不同概念（如左幺元和右幺元）之间的联系来构建证明。
4. 反例的避免：通过证明唯一性来排除其他可能性，这在证明存在性和唯一性时非常重要。

通过这些思想和技巧，我们不仅能够理解特定的数学问题，还能够提高解决其他数学问题的能力。数学思维的培养是一个逐渐积累和深化的过程，需要通过不断的练习和应用来提升。

定理 5-2.2（零元的唯一性）：

在集合 A 上定义的二元运算 ××，如果存在左零元 �1θ1​ 和右零元 �2θ2​，并且 �1=�2θ1​=θ2​，则 A 中的零元是唯一的。

证明过程：

1. 证明左零元和右零元相等：

   • 因为 θ1​ 是左零元，对于所有 x∈A，有 θ1​×x=0。
   • 因为 θ2​ 是右零元，对于所有 x∈A，有 x×θ2​=0。
   • 已知 θ1​=θ2​，所以 θ1​×θ2​=0。
   • 因此，存在唯一的元素 θ=θ1​=θ2​，对所有 x∈A，满足 θ×x=x×θ=0。

2. 证明零元的唯一性：

   • 设 ′θ′ 是 A 中的另一个零元。
   • 由零元的定义，对于所有 x∈A，有 θ′×x=x×θ′=0。
   • 由于 θ 是唯一的满足此性质的元素，所以 θ′=θ。
   • 因此，零元 ′θ′ 必须等于 θ，证明了零元的唯一性。

结论：

定理 5-2.2 证明了如果一个代数结构中存在左零元和右零元，且它们相等，那么存在唯一的零元。这个证明过程显示了逻辑推理在证明数学属性中的重要性，并阐明了代数结构中零元的基本特性。

 定义：

定义 5-2.8（零元）：

• 二元运算：在集合 A 上定义的操作，涉及两个元素的运算，记作 ∗∗。
• 左零元：如果存在一个元素 θ1​∈A 使得对于所有 x∈A，有 θ1​∗x=0，则称 θ1​ 为关于运算 ∗∗ 的左零元。
• 右零元：如果存在一个元素 θ2​∈A 使得对于所有 ∈x∈A，有 2=0x∗θ2​=0，则称 θ2​ 为关于运算 ∗∗ 的右零元。
• 零元：如果一个元素 θ 同时是左零元和右零元，即对所有 x∈A，都有 ∗x=x∗θ=0，则称 θ 为关于运算 ∗∗ 的零元。

解释：

• 零元的含义：零元在给定的二元运算下“吸收”其他所有元素，产生一个固定的结果（通常是集合中的某种形式的“零”）。
• 左零元和右零元的区别：在某些非交换的代数结构中，左零元和右零元可能不相同。左零元影响运算的左侧，而右零元影响运算的右侧。
• 零元的重要性：零元在代数结构中扮演着基本的角色，特别是在环和域等结构中。它提供了一种特殊的运算结果，用于简化运算和公式。

应用实例：

1. 矩阵乘法：零矩阵在矩阵乘法中作为零元，因为任何矩阵与零矩阵相乘都得到零矩阵。
2. 实数加法：在实数集合 R 上，0 是加法运算的零元，因为任何实数加 0 都等于原来的数。

零元的概念在理解和操作复杂代数结构时非常重要。这个定义提供了对代数系统中基本运算和元素关系的重要理解，是构建严密代数系统的关键部分。

定理 5-2.3（幺元与零元的不同性）：

在一个元素个数大于1的代数系统 (A,∗) 中，如果存在幺元 e 和零元 00，则 0=e。

证明过程：

1. 假设：假设 0=e。

2. 使用假设得出矛盾：

   • 对于任意的元素 x∈A，由于 e 是幺元，有 e∗x=x。
   • 同时，由于 00 是零元，有 0∗x=0。
   • 根据假设 0=e，替换 e 为 00 得到 0∗x=x。
   • 因此，对于所有 x∈A，都有 x=0。

3. 得出矛盾：

   • 由于集合 A 中元素的个数大于1，应该存在不同的元素。
   • 但根据上述推理，所有元素都等同于零元 00，这与 A 中含有多个元素相矛盾。

4. 结论：因此，假设 0=e 是错误的，所以幺元 e 和零元 00 必须不相同，即 0=e。

结论：

定理 5-2.3 通过反证法证明了在元素个数大于1的代数系统中，幺元和零元不能是同一个元素。这个证明展示了反证法在数学证明中的有效性，特别是在处理涉及代数系统基本性质的问题时。通过假设相反的情况并导出矛盾，我们能够证明原始命题的正确性。

学到了什么？

数学概念的理解

1. 代数系统的基本元素：理解代数系统中幺元和零元的角色和性质，以及它们在构建数学结构中的重要性。
2. 元素的唯一性：理解特定元素（如幺元和零元）在保证代数系统性质中的独特作用。

证明技巧的学习

1. 反证法：通过假设相反情况来证明原命题，是一种强有力的数学证明方法。
2. 逻辑推理：从假设出发，逐步逻辑推导，直到达到矛盾或结论。
3. 矛盾的识别：在证明过程中，寻找和识别逻辑矛盾是检验假设正确性的关键步骤。

数学思维的培养

1. 假设的检验：在数学中，检验一个假设的有效性是通过寻找其逻辑后果并与已知事实对比。
2. 结构化思考：理解数学结构和其元素之间的关系，如何相互作用和影响整体结构。
3. 细致的分析：认识到即使是看似显而易见的事实（如幺元和零元的不同性质），也需要通过严谨的分析来证明。

数学证明的深层理解

1. 证明的重要性：即使是直观上显而易见的事实，也需要通过逻辑证明来确立。
2. 广泛应用：反证法不仅在数学中广泛使用，也适用于其他科学和哲学领域。

通过学习和理解这些概念和技巧，我们不仅能够更好地理解特定的数学问题，而且还能提高解决更广泛数学问题的能力。数学思维的培养是一个逐步积累和深化的过程，需要通过不断的练习和应用来提升。

数学思想

1. 数学结构的严谨性：数学结构（如代数系统）需要基于严格定义的概念和性质，如幺元和零元。
2. 元素的独立性：在数学结构中，即使某些元素具有相似的性质，它们也可能是独立且不同的，这是数学严谨性的体现。

数学思维

1. 批判性思维：不接受未经证实的陈述，即使它们看起来是显而易见的。
2. 逻辑推理：从一组假设出发，通过逻辑推理达到一个合理的结论。
3. 思维的灵活性：在面对复杂问题时，灵活运用不同的证明方法和技巧。

数学证明方法

1. 反证法：证明某个命题不可能为真，从而证实其相反的命题。这是一种常用且有效的证明技巧。
2. 导出矛盾：通过假设的逻辑后果导出矛盾，从而证明假设是错误的。
3. 抽象和概括：从具体情况抽象出一般性质，增强论证的普适性。

数学证明处理技巧

1. 简化问题：通过将问题分解为更简单或更基本的部分来简化证明。
2. 识别关键性质：确定哪些属性或条件是证明中的关键，并集中注意力在它们上。
3. 避免逻辑错误：在证明的每一步保持逻辑的清晰和准确，避免逻辑上的错误或跳跃。
4. 明确论证：确保每一步论证都是清晰和明确的，使得证明易于理解和跟踪。

通过学习这些证明方法和技巧，我们不仅能够更深入地理解特定的数学概念，还能够提高我们解决其他复杂数学问题的能力。

定义 5-2.9（逆元）：

• 代数系统：考虑一个代数系统 (A,∗)，其中 ∗∗ 是定义在 A 上的二元运算，且 e 是 A 中关于运算 ∗∗ 的幺元。
• 左逆元：如果对于 A 中的元素 a 存在另一个元素 b∈A，使得 b∗a=e，则 b 称为 a 的左逆元。
• 右逆元：如果 a∗b=e 成立，则 b 称为 a 的右逆元。
• 逆元：如果一个元素 b 同时是 a 的左逆元和右逆元，则 b 称为 a 的逆元。
• 互为逆元：如果 b 是 a 的逆元，那么 a 也是 b 的逆元。通常，逆元记作 a−1。

解释：

• 逆元的含义：逆元是在给定的二元运算下“撤销”另一个元素效果的元素。
• 左逆元和右逆元的区别：在非交换代数结构中，左逆元和右逆元可能不相同。左逆元影响运算的左侧，而右逆元影响运算的右侧。
• 逆元的唯一性：在某些代数结构中，如群，每个元素的逆元是唯一的。在更一般的结构中，逆元可能不存在，或存在多个。

应用实例：

1. 群中的逆元：在群结构中，每个元素都有唯一的逆元，无论是左逆元还是右逆元，它们是相同的。
2. 矩阵的逆：在矩阵代数中，如果矩阵 A 有逆矩阵 B，则 AB=BA=I（I 是单位矩阵）。

逆元的概念在代数结构的理解和应用中非常重要。它不仅提供了对于运算如何被“逆转”的直观理解，而且是构建复杂代数系统的关键部分。了解逆元及其性质有助于深入理解群论、环论和域论等数学领域。

定理 5-2.4（逆元的唯一性）：

在代数系统 (A,∗) 中，如果存在幺元 e，每个元素都有左逆元，且运算 ∗∗ 是可结合的，则每个元素的左逆元也是其右逆元，且逆元是唯一的。

证明过程：

1. 左逆元也是右逆元：

   • 设 a,b,c∈A，其中 b 是 a 的左逆元，c 是 b 的左逆元。
   • 因为 b 是 a 的左逆元，所以 b∗a=e。
   • 考虑表达式 c∗(b∗a)∗b：
     • 使用结合律，我们有 c∗((b∗a)∗b)=((c∗b)∗a)∗b。
     • 由于 c∗b=e，表达式简化为 (e∗a)∗b=a∗b。
     • 因为 e 是幺元，e∗a=a，因此 a∗b=a∗b。
   • 由 b∗a=e 和 a∗b=e，可见 b 同时是 a 的左逆元和右逆元。

2. 逆元的唯一性：

   • 假设元素 a 有两个逆元 b 和 c。
   • 那么 b=b∗e=b∗(a∗c)=(b∗a)∗c=e∗c=c。
   • 因此，b=c，说明 a 的逆元是唯一的。

结论：

根据定理 5-2.4 的证明，我们可以得出结论，如果一个代数系统中的运算是可结合的，并且每个元素都有左逆元，则这些左逆元也是相应元素的右逆元，并且逆元是唯一的。这个证明展示了结合律在确定逆元性质方面的重要性，以及如何通过逻辑推理来证明逆元的唯一性。

总结：

重点

1. 基本概念：理解二元运算及其基本性质，包括封闭性、交换性、结合性和分配性。
2. 特殊元素：理解幺元、零元和逆元的定义和它们在代数系统中的角色。
3. 元素性质：明确左幺元、右幺元、左逆元、右逆元的概念以及它们的区别和联系。
4. 运算规律：掌握如何应用这些性质来分析和解决具体的数学问题。

难点

1. 运算性质的区分：正确理解和区分不同的运算性质，尤其是在非交换或非结合的环境中。
2. 逆元的概念：理解逆元并不总是存在，以及逆元可能的不唯一性。
3. 数学证明：理解和应用复杂的数学证明，特别是使用反证法和构造性证明。

易错点

1. 混淆概念：混淆幺元和零元，以及左逆元和右逆元等概念。
2. 逆元的错误假设：错误地假设逆元的存在或唯一性，尤其在非群结构中。
3. 证明的漏洞：在证明过程中忽视关键步骤或逻辑，导致错误的结论。
4. 运算性质的误用：在不适用的情境中误用某些运算性质，如在非交换结构中使用交换律。