8.6 空间曲线及其方程

 

第六节 空间曲线及其方程

一、空间曲线的一般方程

空间曲线通常被定义为两个曲面的交线。假设有两个曲面，它们的方程分别为 𝐹(𝑥,𝑦,𝑧)=0F(x,y,z)=0 和 𝐺(𝑥,𝑦,𝑧)=0G(x,y,z)=0，则这两个曲面的交线 𝐶C 的方程可以表示为方程组：

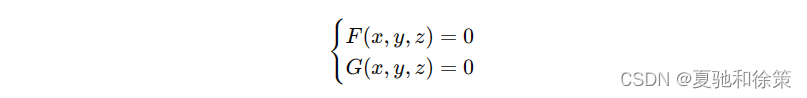
这个方程组称为空间曲线 𝐶C 的一般方程。

例1：解析给定方程组描述的曲线

考虑方程组：

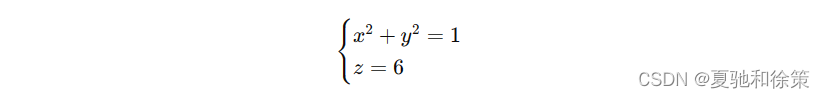
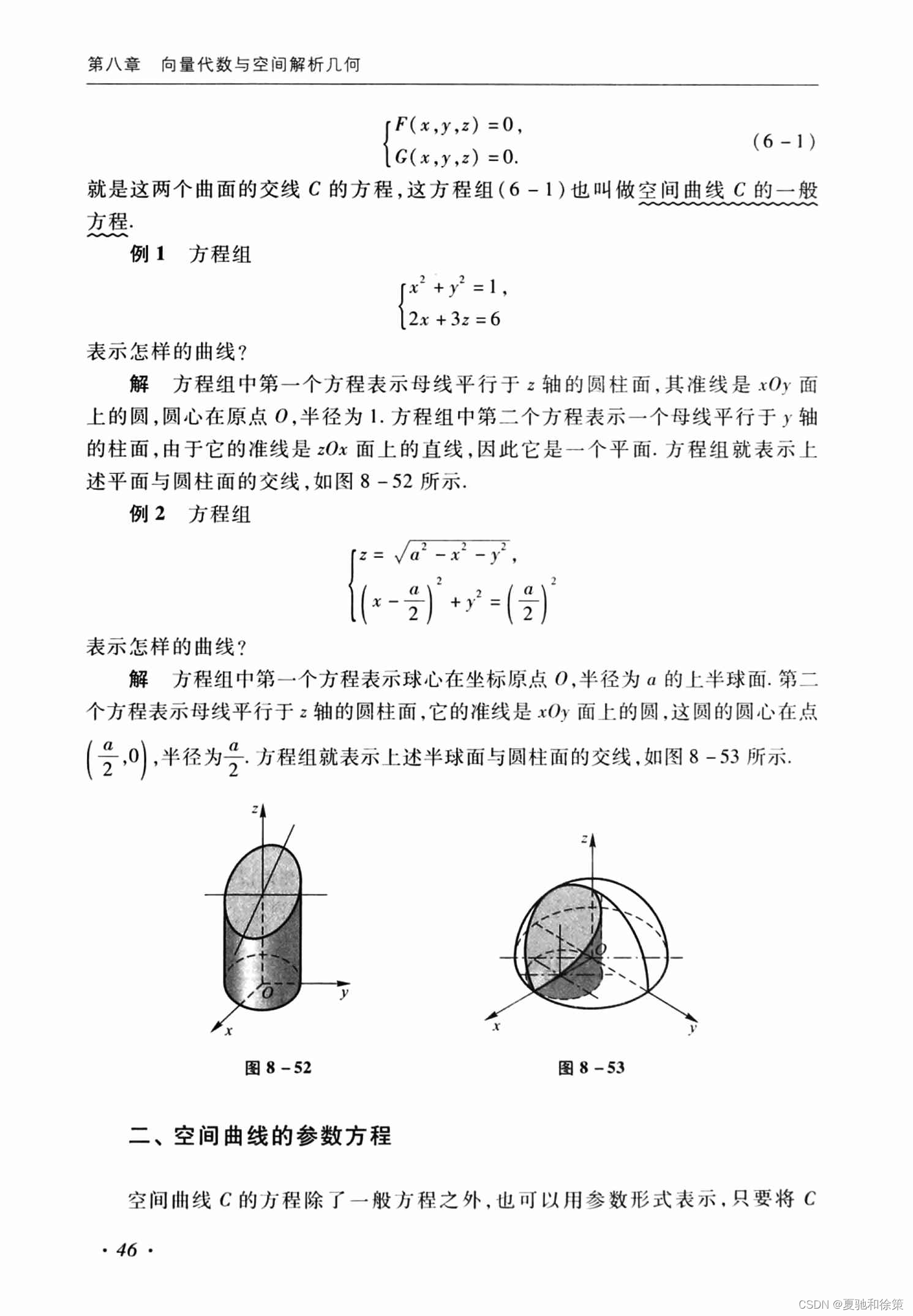
• 第一个方程 𝑥2+𝑦2=1x2+y2=1 描述的是一个母线平行于 𝑧z 轴的圆柱面，其准线为 𝑥𝑂𝑦xOy 面上的圆，圆心在原点 𝑂O，半径为 1。
• 第二个方程 𝑧=6z=6 描述的是一个平面，该平面平行于 𝑥𝑂𝑦xOy 面，并且位于 𝑧z 轴上距原点 6 单位的位置。

因此，这个方程组描述的曲线是圆柱面和平面的交线，即在 𝑧=6z=6 高度处的圆，半径为 1。

例2：解析另一个方程组描述的曲线

考虑方程组：

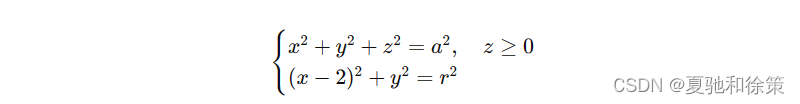
• 第一个方程 𝑥2+𝑦2+𝑧2=𝑎2,𝑧≥0x2+y2+z2=a2,z≥0 描述的是一个球心在坐标原点 𝑂O、半径为 𝑎a 的上半球面。
• 第二个方程 (𝑥−2)2+𝑦2=𝑟2(x−2)2+y2=r2 描述的是一个母线平行于 𝑧z 轴的圆柱面，这个圆柱的准线是 𝑥𝑂𝑦xOy 面上以点 (2,0)(2,0) 为圆心、半径为 𝑟r 的圆。

这个方程组因此描述的是上述半球面与圆柱面的交线，这通常是一个或两个空间曲线的集合，具体形状取决于球和圆柱的相对位置和大小。

这两个例子展示了如何从几何方程中解析出空间曲线的形状和位置，进一步揭示了空间解析几何中曲线和曲面交互的复杂性。

 

 

二、空间曲线的参数方程

螺旋线的参数方程

螺旋线是一种常见的空间曲线，特别是在如螺丝钉这样的应用中。它描述了一个点在绕某个轴旋转的同时，沿该轴线性上升的运动轨迹。

建立参数方程

假设有一个点 𝑀M 初始位于 𝑥x 轴上的位置 𝐴(𝑎,0,0)A(a,0,0)，随着时间 𝑡t 的推移，该点绕 𝑧z 轴旋转并沿 𝑧z 轴向上移动。动点 𝑀M 在平面 𝑥𝑦xy 的投影 𝑀′M′ 的坐标随 𝑡t 变化，其中角速度为 𝜔ω (弧度每秒)，线速度为 𝑣v (单位长度每秒)。

1. 旋转部分：点 𝑀M 绕 𝑧z 轴的旋转可以表示为：

   

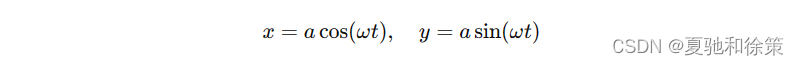
   这里，𝜔𝑡ωt 是从 𝑡=0t=0 时刻开始的旋转角度。

2. 线性上升部分：点 𝑀M 沿 𝑧z 轴的移动可以表示为：

   

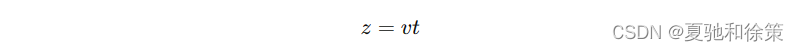
   这里 𝑣v 是沿 𝑧z 轴的上升速度。

因此，螺旋线的参数方程为：

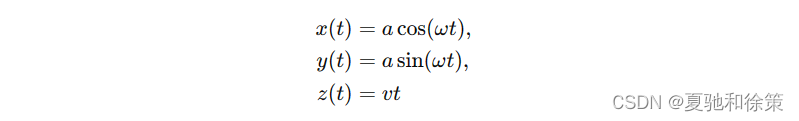
这些方程描述了动点 𝑀M 随时间 𝑡t 在三维空间中的位置。

螺旋线的性质

螺旋线具有重要的几何性质，即每当旋转角 𝜃θ 增加 2𝜋2π（即一周），𝑧z 轴方向的增高恰好为 ℎ=2𝜋𝑣/𝜔h=2πv/ω，这个值称为螺旋线的螺距。螺距是螺旋线在每完成一周时沿 𝑧z 轴的上升高度。

曲面的参数方程

曲面的参数方程通常涉及两个参数，这使得其能够更灵活地描述更复杂的三维表面。例如，固定一个参数 𝑡t 在曲面上定位一个点，而该点绕某轴如 𝑧z 轴旋转时，可得到一个圆形截面。这样，对每个 𝑡t 值，我们能够描述出曲面上的一个圆，其半径取决于 𝑡t。

旋转曲面的参数方程示例

考虑直线 𝑦=𝑚𝑥+𝑐y=mx+c 绕 𝑧z 轴旋转生成的曲面。如果这条直线在 𝑥𝑂𝑧xOz 平面上表达为 𝑧=𝑚𝑥+𝑐z=mx+c，则旋转生成的曲面可以描述为：

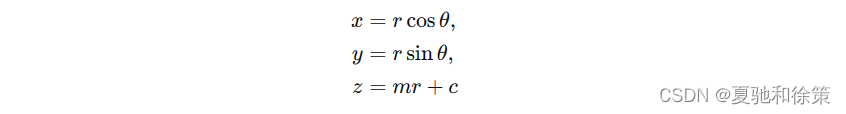
其中 𝑟=𝑥2+𝑦2r=x2+y2​ 是点到 𝑧z 轴的径向距离，𝜃θ 是旋转角。

这种方式通过参数化手段提供了一种非常强大的工具来描述和操作复杂的空间结构。

 

 

 

三、空间曲线在坐标面上的投影

空间曲线 𝐶C 的投影在坐标平面上可以通过消去某个变量来获得。这种投影通常用来分析曲线在某个特定平面上的视图，并且在计算和设计领域非常有用。

投影的理论

考虑空间曲线 𝐶C 的一般方程： 𝐹(𝑥,𝑦,𝑧)=0和𝐺(𝑥,𝑦,𝑧)=0F(x,y,z)=0和G(x,y,z)=0 消去 𝑧z 变量后得到的方程 𝐻(𝑥,𝑦)=0H(x,y)=0 描述了曲线 𝐶C 在 𝑥𝑂𝑦xOy 面上的投影。这个投影曲线被包含在一个母线平行于 𝑧z 轴的柱面内，这个柱面被称为投影柱面。投影柱面与 𝑥𝑂𝑦xOy 平面的交线即为曲线 𝐶C 在 𝑥𝑂𝑦xOy 面上的投影。

例4：球面交线在 𝑥𝑂𝑦xOy 面上的投影方程

考虑两个球面： 𝑥2+𝑦2+𝑧2=1(6-6)x2+y2+z2=1(6-6) 𝑥2+(𝑦−1)2+(𝑧−1)2=1(6-7)x2+(y−1)2+(z−1)2=1(6-7) 求交线 𝐶C 在 𝑥𝑂𝑦xOy 面上的投影。

1. 求柱面方程： 从 6−66−6 减去 6−76−7 并化简，得： 𝑦+𝑧=1y+z=1 代入 𝑧=1−𝑦z=1−y 到任一球面方程中（这里用 6−66−6）： 𝑥2+𝑦2+(1−𝑦)2=1x2+y2+(1−y)2=1 化简得： 𝑥2+2𝑦2−2𝑦=0x2+2y2−2y=0 这是交线 𝐶C 在 𝑥𝑂𝑦xOy 面的投影柱面方程。

2. 投影方程： 简化得到 𝑥𝑂𝑦xOy 平面的投影方程： 𝑥2+2𝑦2−2𝑦=0x2+2y2−2y=0 这可以进一步化简和重写以更清楚地表达投影的形状。

例5：立体在 𝑥𝑂𝑦xOy 面上的投影

设立体由上半球面 𝑧=4−𝑥2−𝑦2z=4−x2−y2​ 和锥面 𝑧=3(𝑥2+𝑦2)z=3(x2+y2)​ 围成。求该立体在 𝑥𝑂𝑦xOy 面上的投影。

1. 交线方程： 4−𝑥2−𝑦2=3(𝑥2+𝑦2)4−x2−y2​=3(x2+y2)​ 平方后解得： 4−𝑥2−𝑦2=3(𝑥2+𝑦2)4−x2−y2=3(x2+y2) 4=4(𝑥2+𝑦2)4=4(x2+y2) 𝑥2+𝑦2=1x2+y2=1 这是一个母线平行于 𝑧z 轴的圆柱面。

2. 投影曲线： 交线 𝐶C 在 𝑥𝑂𝑦xOy 面上的投影是圆 𝑥2+𝑦2=1x2+y2=1。

这些例子展示了如何通过简化和重组方程来获得空间曲线或立体在坐标面上的投影，这在多种工程和科学问题中都是一个非常有用的技术。