POJ 1179 区间DP

Description

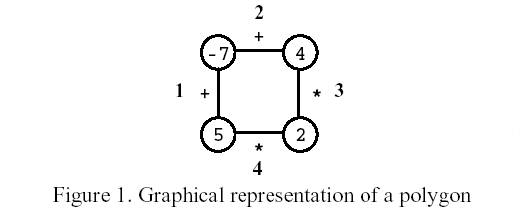
Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered from 1 to N.

On the first move, one of the edges is removed. Subsequent moves involve the following steps:
�pick an edge E and the two vertices V1 and V2 that are linked by E; and
�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2.
The game ends when there are no more edges, and its score is the label of the single vertex remaining.

Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0.

Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score.

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *).

3 <= N <= 50
For any sequence of moves, vertex labels are in the range [-32768,32767].

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

 

题意：给出一些边和一些点，每个点上有一个数，每个边上有一个符号，一开始先任意去掉一条边，然后从剩下的n个点，n-1条边中删掉一条边，计算与这条边相邻的两个点的值（运算为加或者乘，取决于边代表了加或乘）。要求求出按这种方法计算能得到的最大值，并输出一开始删的是那条边

区间DP问题dp,用dp[i][j] 表示从第i个点到第j个点区间内进行计算能得到的最大值，转移方程就是

 

dp[i][j] = max{dp[i][k](*或+，取决于从k到k+1的符号)dp[k+1][j]} (i =< k <= j-2);

但光这样就错了，因为没考虑负负得正的情况（本弱就没考虑）。应该在开一个数组dp2记录每次合并的到的最小值，最小值可以由两个区间分别取最小值转移过来，也可以一个取最小，一个取最大转移来，也可以一个取最大，一个取最小转移来（但这三种里面选两种就能过，不知道是不是数据太弱）；最大值可以由两个最小或者两个最大值转移过来，最后解决时在最内层循环多加几条语句就好了。

 

下面是代码：

 

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <ctype.h>
#include <cstring>
#include <string>
#include <queue>
#include <cmath>

#define MAXN 110
#define INF 2100000000
#define pu system("pause")

#pragma comment(linker, "/STACK:16777216");

using namespace std;

int n;
char a[MAXN][MAXN];
int val[MAXN];
int dp[MAXN][MAXN];
int dp2[MAXN][MAXN];
int cal(int n1, int n2, char c)
{
    if(c == 't') return n1+n2;
    else return n1*n2;
}
int main()
{
    //freopen("C:/Users/Admin/Desktop/in.txt", "r", stdin);
    cin >> n;
    cin >> a[n-1][n];
    cin >> val[0];
    for(int i = 0; i < n-1; i++)
    {
        cin >> a[i][i+1];
        cin >> val[i+1];
    }
    for(int i = n; i < 2*n-1; i++)
    {
        a[i][i+1] = a[i-n][i-n+1];
        val[i] = val[i-n];
    }
    val[2*n-1] = val[n-1];
    memset(dp, -127, sizeof(dp));
    memset(dp2, 127, sizeof(dp2));
    for(int i = 0; i < 2*n; i++)
    {
        dp[i][i] = val[i];
        dp2[i][i] = val[i];
    }
    for(int start = 0; start < n; start++)
    {
        for(int i = 1; i < n; i++)
        {
            //dp[i-1][i] = cal(val[i-1], val[i], a[i-1][i]);
            for(int j = start; j < 2*n-i; j++)
            {

                //区间为j~j+i
                for(int k = j; k < j+i; k++)
                {
                    //底下三种任意选两种都可以，不知道什么情况
                    //dp2[j][j+i] = min(cal(dp[j][k], dp2[k+1][j+i], a[k][k+1]), dp2[j][j+i]);
                    dp2[j][j+i] = min(cal(dp2[j][k], dp[k+1][j+i], a[k][k+1]), dp2[j][j+i]);
                    dp2[j][j+i] = min(cal(dp2[j][k], dp2[k+1][j+i], a[k][k+1]), dp2[j][j+i]);

                    dp[j][j+i] = max(cal(dp[j][k], dp[k+1][j+i], a[k][k+1]), dp[j][j+i]);
                    dp[j][j+i] = max(cal(dp2[j][k], dp2[k+1][j+i], a[k][k+1]), dp[j][j+i]);
                }
            }
        }
    }
    int ans = dp[0][n-1];
    int p[MAXN], cp = 0;
    for(int start = 0; start < n; start++)
    {
        ans = max(ans, dp[start][start+n-1]);
    }
    for(int i = 0; i < n; i++)
    {
        if(dp[i][i+n-1] == ans)
        {
            p[cp++] = i+1;
        }
    }
    cout << ans << endl;
    for(int i = 0; i < cp; i++)
    {
        if(i != 0) cout << " ";
        cout << p[i];
    }
    cout << endl;

    return 0;
}