CloudCompare源码分析_八叉树（Octree）算法基础CC中的八叉树结构

官方参考地址：CloudCompare octree - CloudCompareWiki

CC的octree算法主要体现在DgmOctree.h和DgmOctree.cpp中，他采用了一种分级的结构，最大支持21级，如下，

static const int MAX_OCTREE_LEVEL = 21;

然后，会事先计算得到一个分级表，

预先计算好的数据表

CC这么做的原因是，把事先能计算好的数据先存储起来，用空间换时间的办法，来加速运算速度。

(1) PRE_COMPUTED_BIT_SHIFT_VALUES

//! Pre-computed bit shift values (one for each level)
struct BitShiftValues
{
    //! Default initialization
    BitShiftValues()
    {
        //we compute all possible values
        for (unsigned char level = 0; level <= DgmOctree::MAX_OCTREE_LEVEL; ++level)
        {
            values[level] = (3 * (DgmOctree::MAX_OCTREE_LEVEL - level));
        }
    }

    //! Values
    unsigned char values[DgmOctree::MAX_OCTREE_LEVEL+1];
};
static BitShiftValues PRE_COMPUTED_BIT_SHIFT_VALUES;

unsigned char DgmOctree::GET_BIT_SHIFT(unsigned char level)
{
    //return (3 * (DgmOctree::MAX_OCTREE_LEVEL - level));
    return PRE_COMPUTED_BIT_SHIFT_VALUES.values[level];
}

所以这个value实际相当于这样一个表，

[0]    63
[1]    60
[2]    57
[3]    54
[4]    51
[5]    48
[6]    45
[7]    42
[8]    39
[9]    36
[10]    33
[11]    30
[12]    27
[13]    24
[14]    21
[15]    18
[16]    15
[17]    12
[18]    9
[19]    6
[20]    3
[21]    0

(2) PRE_COMPUTED_POS_CODES

static const int MAX_OCTREE_LENGTH = (1 << MAX_OCTREE_LEVEL);

//! Pre-computed cell codes for all potential cell positions (along a unique dimension)
struct MonoDimensionalCellCodes
{
    //! Total number of positions/values
    /** There are 1024 possible values at level 10, and 2M. at level 21.
        \warning Never pass a 'constant initializer' by reference
    **/
    static const int VALUE_COUNT = DgmOctree::MAX_OCTREE_LENGTH;

    //! Default initialization
    MonoDimensionalCellCodes()
    {
        //we compute all possible values for cell codes
        //(along a unique dimension, the other ones are just shifted)
        for (int value = 0; value < VALUE_COUNT; ++value)
        {
            int mask = VALUE_COUNT;
            DgmOctree::CellCode code = 0;
            for (unsigned char k = 0; k < DgmOctree::MAX_OCTREE_LEVEL; k++)
            {
                mask >>= 1;
                code <<= 3;
                if (value & mask)
                {
                    code |= 1;
                }
            }
            values[value] = code;
        }

        //we compute all possible masks as well! (all dimensions)
        //DgmOctree::CellCode baseMask = (1 << (3 * DgmOctree::MAX_OCTREE_LEVEL));
        //for (int level = DgmOctree::MAX_OCTREE_LEVEL; level >= 0; --level)
        //{
        //    masks[level] = baseMask - 1;
        //    baseMask >>= 3;
        //}
    }

    //! Mono-dimensional cell codes
    DgmOctree::CellCode values[VALUE_COUNT];

    //! Mono-dimensional cell masks
    //DgmOctree::CellCode masks[DgmOctree::MAX_OCTREE_LEVEL + 1];
};
static MonoDimensionalCellCodes PRE_COMPUTED_POS_CODES;

这里，MAX_OCTREE_LENGTH == (1<<21) == 2097152 == 0x200000 ，是一个位置的极限值，这个表实际上相当于，

[0]    0
[1]    1
[2]    8
[3]    9
[4]    64
[5]    65
[6]    72
[7]    73
[8]    512
[9]    513
[10]    520
[11]    521
[12]    576
[13]    577
[14]    584
[15]    585
[16]    4096
[17]    4097
[18]    4104
[19]    4105
[20]    4160
[21]    4161
[22]    4168
[23]    4169
[24]    4608
[25]    4609
[26]    4616
[27]    4617
[28]    4672
[29]    4673
[30]    4680
[31]    4681
......

计算基础之cellCode

在设计算法之前，我们需要了解一下OcTree层级的概念。

比如我的所有点都在一个64x64x64的立方体内，那第0层级的边长就是64，也就是最大的cube框的边长，那么一个立方体包含8个cube框，下一级第1层级框的边长大小就是64/2，依此类推，再下一级就是64/4，64/8......

另外，给一个相关讲解的参考地址，

参考：数据立方体_点云空间数据组织——八叉树-白红宇的个人博客

作者对八叉树进行了讲解，我摘录了其中的一点。如下，

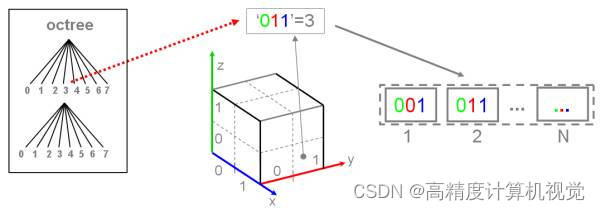
八叉树将空间分割成八块，根据2进制， 3位2进制即可表示8个数字，3位中的顺序:zyx ，顺序区分，从小递增到大，如： 011，即z为0，x为1，y为 1的块位置。所以 64位操作系统最多可分割为64/3 = 21级， 32位操作系统最多可分割为32/3 = 10级。

建立单维索引( CellCode)

将原有的1位2进制转为3位，如：001转为000 000 001，010 转为 000 001 000，以此类推。另外两个维度的code分别左移1位和2位即可。

软件初始化时就计算完了所有CellCode。

具体可参考前面讲到的结构体
static MonoDimensionalCellCodes PRE_COMPUTED_POS_CODES;

好了，前面的这个要怎么理解和使用呢？

比如，我计算得到cellPos=(2,2,2)，那
PRE_COMPUTED_POS_CODES.values[2] == 8 == 000 001 000
假设对应的层级也是21，那么，GenerateTruncatedCellCode中，返回的数据结果就是

return    (
     PRE_COMPUTED_POS_CODES.values[cellPos.x << shift]
|    (PRE_COMPUTED_POS_CODES.values[cellPos.y << shift] << 1)
|    (PRE_COMPUTED_POS_CODES.values[cellPos.z << shift] << 2)
) >> GET_BIT_SHIFT(level);

具体可以参考DgmOctree::GenerateTruncatedCellCode函数。
也就是
000 001 000 | 000 001 000 << 1 | 000 001 000 << 2 == 000 111 000

再比如，我计算得到cellPos=(3,3,3)，那
PRE_COMPUTED_POS_CODES.values[3] == 9 == 000 001 001
那么，在21级，相应的cellcode就是
000 001 001 | 000 001 001 << 1 | 000 001 001 << 2 == 000 111 111

又比如，我计算得到cellPos=(4,4,4)，那
PRE_COMPUTED_POS_CODES.values[3] == 64 == 001 000 000
那么，在21级，相应的cellcode就是
001 000 000 | 001 000 000 << 1 | 001 000 000 << 2 == 111 000 000

看出规律了吗？

作者的意思，就是要设计一个像c++中std::map这样的一个结构，能够迅速通过这个cellCode，找到任意层级的cellPos。

例如，前面在第21层级的cellPos=(4,4,4)，到了第20层级，就要右移3位，因为

GET_BIT_SHIFT(20) == 3

不难判断，这个cellCode对应的cellPos正是(2,2,2)。

好了，有了这些相关基础知识之后， 我们开始讲解点云的八叉树算法的架构与原理。

ccPointCloud : ccGenericPointCloud

class QCC_DB_LIB_API ccPointCloud : public CCCoreLib::PointCloudTpl<ccGenericPointCloud, QString>
{
}

这里，ccGenericPointCloud的父类是GenericIndexedCloudPersist

class QCC_DB_LIB_API ccGenericPointCloud : public ccShiftedObject,  public CCCoreLib::GenericIndexedCloudPersist
{
    friend class ccMesh;

这是一个纯虚类，GenericIndexedCloudPersist，其所有的上级父类也都是纯虚类，或者说是接口，包括GenericIndexedCloud，GenericIndexedCloud， 以及GenericCloud，

class CC_CORE_LIB_API GenericIndexedCloudPersist : virtual public GenericIndexedCloud
{
    ......
}

class CC_CORE_LIB_API GenericIndexedCloud : virtual public GenericCloud {
    ......
}

class CC_CORE_LIB_API GenericCloud{
    ......
}

计算过程（程序结构）

当在CloudCompare中按下Edit-->Octree-->Compute之后，就会启动ocTree的计算，

void MainWindow::doActionComputeOctree()
{
    if ( !ccEntityAction::computeOctree(m_selectedEntities, this) )
        return;

    refreshAll();
    updateUI();
}

computeOctree会对所有选中的实际进行计算，在该函数中，先是得到entity的点云clouds，然后逐个对其进行计算，octree = cloud->computeOctree(..)，或者直接生成octree = ccOctree::Shared(new ccOctree(cloud))，

bool computeOctree(const ccHObject::Container &selectedEntities, QWidget* parent)
{

    for (ccHObject* ent : selectedEntities)
    {
        ......
        ccGenericPointCloud* cloud = ccHObjectCaster::ToGenericPointCloud(ent, &lockedVertices);
        ......
        clouds.insert(cloud);
        ......
    }

    .......
    for (const auto cloud : clouds)
    {
        ......
        switch (coDlg.getMode())
        {
        case ccComputeOctreeDlg::DEFAULT:
            octree = cloud->computeOctree(&pDlg);
            break;
        case ccComputeOctreeDlg::MIN_CELL_SIZE:
        case ccComputeOctreeDlg::CUSTOM_BBOX:
        {
            ......
            octree = ccOctree::Shared(new ccOctree(cloud));
            ......
        }
        break;
        }
    }
    ......
}

接下，调用ccGenericPointCloud::computeOctree，

ccOctree::Shared ccGenericPointCloud::computeOctree(CCCoreLib::GenericProgressCallback* progressCb, bool autoAddChild/*=true*/)
{
    deleteOctree();

    ccOctree::Shared octree = ccOctree::Shared(new ccOctree(this));
    if (octree->build(progressCb) > 0)
    {
        setOctree(octree, autoAddChild);
    }
    else
    {
        octree.clear();
    }

    return octree;
}

在这里面，会先new出一个ccOcTree，并把this也就是ccGenericPointCloud传入进去给m_theAssociatedCloud，然后通过build进行octree的计算，

int DgmOctree::build(GenericProgressCallback* progressCb)
{
    if (!m_theAssociatedCloud)
    {
        assert(false);
        return -1;
    }

    if (!m_thePointsAndTheirCellCodes.empty())
    {
        clear();
    }

    m_theAssociatedCloud->getBoundingBox(m_pointsMin, m_pointsMax);

    m_dimMin = m_pointsMin;
    m_dimMax = m_pointsMax;

    //we make this bounding-box cubical (+0.1% growth to avoid round-off issues when projecting points in the octree)
    CCMiscTools::MakeMinAndMaxCubical(m_dimMin, m_dimMax, 0.001);

    return genericBuild(progressCb);
}

这里要注意，ccOctree的父类正是DgmOctree，

class QCC_DB_LIB_API ccOctree : public QObject, public CCCoreLib::DgmOctree

计算OcTree

结构体IndexAndCode中，给出的是点的index和所在的cube的code，大体上是这样定义的，

    struct IndexAndCode
    {
        //! index
        unsigned theIndex;
        //! cell code
        CellCode theCode;
        ......
    }

    using cellsContainer = std::vector<IndexAndCode>;

    //! The coded octree structure
    cellsContainer m_thePointsAndTheirCellCodes;

接下来我们看一下DgmOctree::genericBuild函数的主体，

int DgmOctree::genericBuild(GenericProgressCallback* progressCb)
{
    ......
    try
    {
        m_thePointsAndTheirCellCodes.resize(pointCount); 
    }
    ......

    updateCellSizeTable();


    //for all points
    cellsContainer::iterator it = m_thePointsAndTheirCellCodes.begin();
    for (unsigned i = 0; i < pointCount; i++)
    {
        const CCVector3* P = m_theAssociatedCloud->getPoint(i);

        //does the point falls in the 'accepted points' box?
        //(potentially different from the octree box - see DgmOctree::build)
        if (    (P->x >= m_pointsMin[0]) && (P->x <= m_pointsMax[0])
            &&    (P->y >= m_pointsMin[1]) && (P->y <= m_pointsMax[1])
            &&    (P->z >= m_pointsMin[2]) && (P->z <= m_pointsMax[2]) )
        {
            //compute the position of the cell that includes this point
            Tuple3i cellPos;
            getTheCellPosWhichIncludesThePoint(P, cellPos);

            ......

            it->theIndex = i;
            it->theCode = GenerateTruncatedCellCode(cellPos, MAX_OCTREE_LEVEL);
            ......

            ++it;
            ++m_numberOfProjectedPoints;
        }

    ......

    //we sort the 'cells' by ascending code order
    ParallelSort(m_thePointsAndTheirCellCodes.begin(), m_thePointsAndTheirCellCodes.end(), IndexAndCode::codeComp);

    //update the pre-computed 'number of cells per level of subdivision' array
    updateCellCountTable();

    ......    
}

下面我们来看这个函数是如何计算octree的，

(1) 函数中先是通过m_thePointsAndTheirCellCodes.resize分配内存，

m_thePointsAndTheirCellCodes.resize(pointCount); 

（2）然后，通过updateCellSizeTable不断分割尺寸，得到每一级cube框的大小，例如，假设最大的框的边长为64，那么一个立方体包含8个cube框，下一级框的边长大小就是64/2，依此类推，再下一级就是64/4，64/8......

void DgmOctree::updateCellSizeTable()
{
    //update the cell dimension for each subdivision level
    m_cellSize[0] = m_dimMax.x - m_dimMin.x;

    unsigned long long d = 1;
    for (int k = 1; k <= MAX_OCTREE_LEVEL; k++)
    {
        d <<= 1;
        m_cellSize[k] = m_cellSize[0] / d;
    }
}

然后，函数开始逐个点逐个点地计算。

(3) 通过getTheCellPosWhichIncludesThePoint计算点的cellPos。这里的cellPos是指最小的cube的序号，和前面的讲解一样，假设0级cell大小是64，那么第20级的cell大小就是cs = 64/2^20 = 0.00006103515625，那么在某个维度上其序号就是(x-xmin)/cs，如下，

//! Type of the coordinates of a (N-D) point
using PointCoordinateType = float;

//! Returns the position FOR THE DEEPEST LEVEL OF SUBDIVISION of the cell that includes a given point
    /** The cell coordinates can be negative or greater than 2^MAX_OCTREE_LEVEL-1
    as the point can lie outside the octree bounding-box.
    \param thePoint the query point
    \param cellPos the computed position
    **/
inline void getTheCellPosWhichIncludesThePoint(const CCVector3* thePoint, Tuple3i& cellPos) const
{
    const PointCoordinateType& cs = getCellSize(MAX_OCTREE_LEVEL);
    //DGM: if we admit that cs >= 0, then the 'floor' operator is useless (int cast = truncation)
    cellPos.x = static_cast<int>(/*floor*/(thePoint->x - m_dimMin.x) / cs);
    cellPos.y = static_cast<int>(/*floor*/(thePoint->y - m_dimMin.y) / cs);
    cellPos.z = static_cast<int>(/*floor*/(thePoint->z - m_dimMin.z) / cs);
}

(4) 获取点的cellCode，

这个，是我们在基础部分讲过的函数DgmOctree::GenerateTruncatedCellCode，

DgmOctree::CellCode DgmOctree::GenerateTruncatedCellCode(const Tuple3i& cellPos, unsigned char level)
{
    assert(cellPos.x >= 0 && cellPos.x < MonoDimensionalCellCodes::VALUE_COUNT
    &&cellPos.y >= 0 && cellPos.y < MonoDimensionalCellCodes::VALUE_COUNT
    &&cellPos.z >= 0 && cellPos.z < MonoDimensionalCellCodes::VALUE_COUNT);

    const unsigned char shift = MAX_OCTREE_LEVEL - level;

    return(PRE_COMPUTED_POS_CODES.values[cellPos.x << shift]
          |(PRE_COMPUTED_POS_CODES.values[cellPos.y << shift] << 1)
          |(PRE_COMPUTED_POS_CODES.values[cellPos.z << shift] << 2)
    ) >> GET_BIT_SHIFT(level);
}

(5)按cellCode大小排序

ParallelSort(m_thePointsAndTheirCellCodes.begin(), m_thePointsAndTheirCellCodes.end(), IndexAndCode::codeComp);

值得说明的是，在函数中，对变量m_fillIndexes也进行了计算，因为源码比较简单，一目了然，这里就不展开讲了。

本文结束。