uva 12627 Erratic Expansion

原题：
Piotr found a magical box in heaven. Its magic power is that if you place any red balloon inside it
then, after one hour, it will multiply to form 3 red and 1 blue colored balloons. Then in the next hour,
each of the red balloons will multiply in the same fashion, but the blue one will multiply to form 4 blue
balloons. This trend will continue indefinitely. The arrangements of the balloons after the 0-th, 1-st, 2-nd and 3-rd hour are depicted in the following diagram.

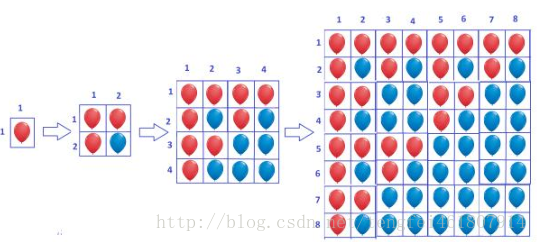
As you can see, a red balloon in the cell (i,j) (that is i-th row and j-th column) will multiply to
produce 3 red balloons in the cells (i ∗ 2 − 1,j ∗ 2 − 1), (i ∗ 2 − 1,j ∗ 2), (i ∗ 2,j ∗ 2 − 1) and a blue
balloon in the cell (i∗2,j ∗2). Whereas, a blue balloon in the cell (i,j) will multiply to produce 4 blue
balloons in the cells (i∗2−1,j ∗2−1), (i∗2−1,j ∗2), (i∗2,j ∗2−1) and (i∗2,j ∗2). The grid size
doubles (in both the direction) after every hour in order to accommodate the extra balloons.
In this problem, Piotr is only interested in the count of the red balloons; more specifically, he would
like to know the total number of red balloons in all the rows from A to B after K-th hour.
Input
The first line of input is an integer T (T < 1000) that indicates the number of test cases. Each case
contains 3 integers K, A and B. The meanings of these variables are mentioned above. K will be in
the range [0,30] and 1 ≤ A ≤ B ≤ 2 K .
Output
For each case, output the case number followed by the total number of red balloons in rows [A,B] after
K-th hour.
Sample Input
3
0 1 1
3 1 8
3 3 7
Sample Output
Case 1: 1
Case 2: 27
Case 3: 14

中文：
给你一个二维网格，一开始有一个红气球，一个红球没隔一个小时可以分裂成三个红气球和一个蓝气球，蓝气球在右下角。
问你最后在k个小时以后，第a行到b行之间有多少个红气球。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll K,A,B;
ll power3[31],power2[31];


ll dfs(ll i,ll j)//i小时  j行
{
    if(j<=0)
        return 0;
    if(i==0)
        return 1;
    if(j<=power2[i-1])
        return dfs(i-1,j)*2;
    else
        return power3[i-1]*2+dfs(i-1,j-power2[i-1]);
}

int main()
{
    ios::sync_with_stdio(false);
    power2[0]=power3[0]=1;
    for(int i=1;i<=30;i++)
    {
        power3[i]=power3[i-1]*3;
        power2[i]=power2[i-1]*2;
    }
    int t;
    cin>>t;
    int k=1;
    while(t--)
    {
        cin>>K>>A>>B;
        cout<<"Case "<<k++<<": "<<dfs(K,B)-dfs(K,A-1)<<endl;
    }
    return 0;
}

解答：

紫书上面的例题

规律很好找，设第n个图的样式为f(n)，那么如图，X代表蓝气球

由于n值可以取到30，所以没有办法打表，只能一个一个的算。

设dfs(i,j)为第i个小时的以后，前j行的红气球数。

分成两种情况，当j大于$2^{n-1}$时，红气球的个数可以递推给$3^{n-1}×2+dfs(i-1,j-2^{n-1})$

其中$3^{n-1}$是f(n-1)的图样式时红气球的个数，很好理解。

当j小于$2^{n-1}$时，红气球的个数可以递推为$2×dfs(i-1,j)$