KMP&扩展KMP学习笔记（多图预警）

最新推荐文章于 2020-07-20 18:00:08 发布

ILoveFujibayashiRyou

最新推荐文章于 2020-07-20 18:00:08 发布

阅读量532

点赞数 3

分类专栏： C++模板系列文章标签： KMP 字符串匹配毒瘤失配数组

本文链接：https://blog.csdn.net/the_oier/article/details/102765796

版权

C++模板系列专栏收录该内容

11 篇文章 0 订阅

订阅专栏

震惊，KMP加上扩展KMP的学习笔记字数竟然破万了（令人窒息）

KMP部分

例子：一个文本串A，一个模式串B，A的长度为n，B的长度为m，求B在A中出现的位置。（ $n,m<=10^6$ ）
题目链接：洛咕3375 【模板】kmp字符串匹配
暴力：枚举文本串中的位置 $i$ ，暴力比较A的 $[i, i + m - 1]$ 这个区间是否与B相同。时间复杂度最坏情况是A，B都只有一种字符（比如A是aaaaa，B是aaa），此时时间复杂度为 $O (n m)$ 。
燃鹅 $n,m<=10^6$ ，所以要优化到线性。

发现暴力比较的过程中有很多冗余的操作，所以考虑优化这个过程。

一、next数组

令 $n e x t [i]$ 表示模式串B中，假设前缀 $[1, i]$ 构成的字符串为 $a$ ，使 $a$ 的前缀与后缀相同的最大长度，不算前、后缀为 $a$ 本身的情况（也就是规定 $n e x t [i] < i$ ）。
其中字符串 $s$ 的前缀 $[1, i]$ 表示 $s_1s_2...s_i$ ，后缀 $[i, n]$ 表示 $s_is_{i+1}...s_n$

例子：字符串为ABABA。
珂以得出， $n e x t [1] = 0, n e x t [2] = 0, n e x t [3] = 1, n e x t [4] = 2, n e x t [5] = 3$ 。
next[1]：考虑的是 $" A "$ 。因为前、后缀不能取整个字符串，所以next[1]=0
next[2]：考虑的是 $" A B "$ 。因为 $" A "$ 不等于 $" B "$ ，所以next[2]=0
next[3]：考虑的是 $" A B A "$ 。最长前、后缀相等的长度为1，此时前缀为 $" A "$ ，后缀为 $" A "$ 。前、后缀相等的长度不能为2，因为长度为2的前缀为 $" A B "$ ，后缀为"BA"。
next[4]：考虑的是 $" A B A B " 。$ 前、后缀长度均为2时，前、后缀均为 $" A B "$ 。前、后缀长度为3时，前缀为 $" A B A "$ ，后缀为 $" B A B "$ 。
next[5]：考虑的是 $" A B A B A "$ 。同理珂得，使前、后缀相同的最大长度为3，即前后缀均为 $" A B A "$ 。

求出next数组的方式：
让B自己与自己比较：
比如 $B = " A B A B A "$ ，现在要求出它的next[5]。
由于不能前、后缀为整个字符串，所以先把第二个B串往右移一格：

ABABA
 ABABA

忽略空出的部分，那么珂以发现，比较的是第一个B串的后缀 $" B A B A "$ ，和第二个B串的 $" A B A B "$ 。
发现并不相同，所以再把第二个B串往右移一格：

ABABA
  ABABA

同样地比较两串都非空的部分，即比较A串的后缀"ABA"和B串的前缀"ABA"。
因为后缀和前缀相同，所以next[5]=3。

正确性证明：
让B串和自己比较，把第二个B串往右移动一格，那么非空部分就分别表示第一个B串的后缀和第二个B串的前缀，然后让第一个B串的后缀和第二个B串的前缀比较。
如果第一个B串的后缀和第二个B串的前缀相同，那么表示这个长度是最大的能让B串的前后缀相同的长度。

然鹅这样仍然不是线性，所以还要优化：
假设对于一个字符串，需要求出 $n e x t [i]$ 的值。
考虑一个一个把字符加进去，那么现在已经加入了前 $i - 1$ 个字符（如图所示）。
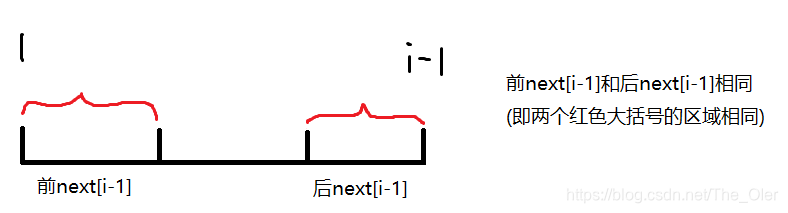
由 $n e x t$ 数组的定义，这个字符串的前 $n e x t [i - 1]$ 个字符和后 $n e x t [i - 1]$ 个字符相同（如图所示）。
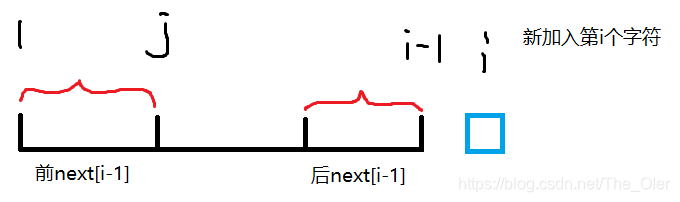
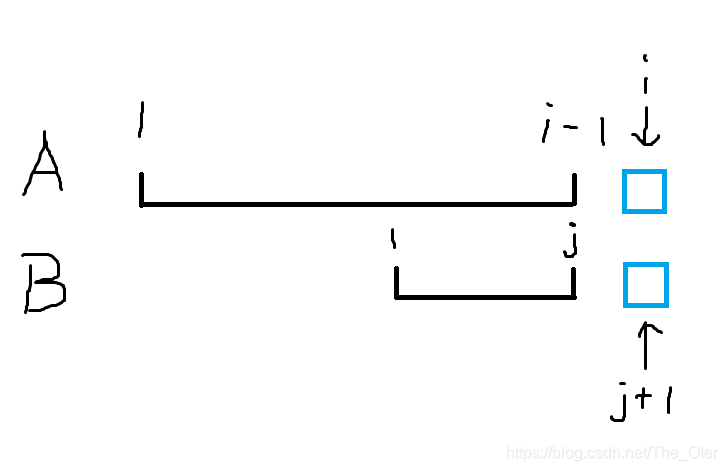
在这里插入图片描述
然后加入第 $i$ 个字符，如图，蓝色方框表示第 $i$ 个字符。令 $j = n e x t [i - 1]$ 。

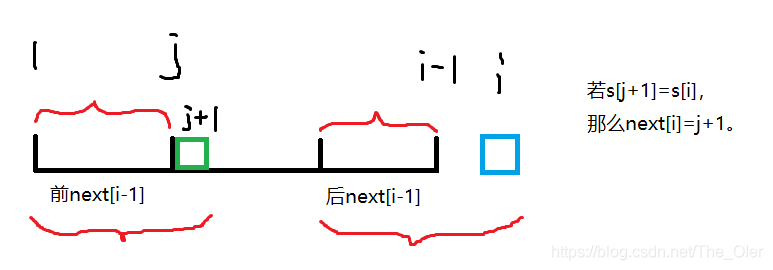
情况1：第 $j + 1$ 个字符与第 $i$ 个字符相同
因为 $n e x t [i - 1]$ 已经是让前 $i - 1$ 个字符的前、后缀相同的最大长度，
因为 $j = n e x t [i - 1]$ ，所以若第 $j + 1$ 个字符与第 $i$ 个字符相同，则 $n e x t [i] = j + 1$ 。
证明：若存在比 $j + 1$ 更长的长度，使前 $i$ 个字符前、后缀相同，那么 $n e x t [i - 1]$ 不是最大长度，所以矛盾。
因此这样有正确性qwq。
在这里插入图片描述
情况2：第 $j + 1$ 个字符与第 $i$ 个字符不相同
然后考虑一个孙臭的情况：第 $j + 1$ 个字符和第 $i$ 个字符不同。
这种情况 $j + 1$ 不符合（因为前后缀不一样）。
珂以证明，最长的长度一定不超过 $j$ ：
若有比 $j$ 更长的长度使前 $i$ 个字符的前后缀相同，则假设长度为 $k$ 。
根据 $n e x t$ 数组的定义，前 $k$ 个字符与后 $k$ 个字符相同，那么珂以推出前 $k - 1$ 个字符与倒数第 $k$ 个字符至第 $i - 1$ 个字符相同，所以 $n e x t [i - 1] = k - 1$ （因为 $k > j$ ），与 $n e x t [i - 1] = j$ 矛盾。
因此 $next[i]\le j$ 。

所以我们需要从 $1$ 到 $j$ 中找到一个长度，使得 $i$ 个字符中，前 $k$ 个字符和后 $k$ 个字符相同。
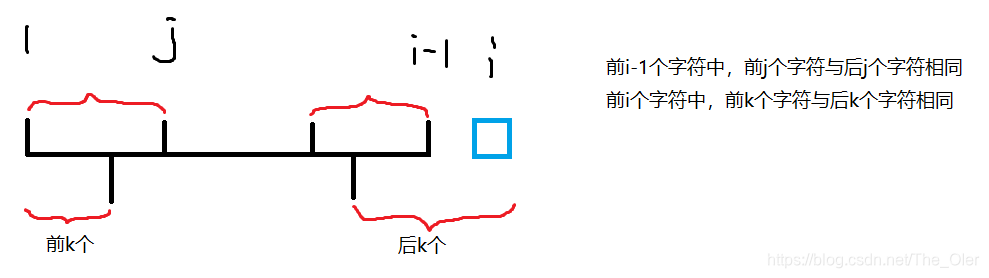
不妨去掉“前 $k$ 个字符”与“后 $k$ 个字符”两者的最后一个字符，即前 $k - 1$ 个字符与倒数第 $k$ 个字符至第 $i - 1$ 个字符分别相等（如图所示）。
在这里插入图片描述
所以，前 $j$ 个字符中，长度为 $k - 1$ 的前缀、后缀相等。
next数组的定义： $n e x t [j]$ 表示使前 $j$ 个字符前缀、后缀相等的最大长度。
所以此时我们让 $j = k$ ，然后检验第 $k + 1$ 个字符是否与 $i$ 相等。
如果相等那么回到情况1，否则回到情况2。
代码实现：

int j=0;
for(int i=2; i<=n; i++) {	//next[1]=0
	//此时j存储的使next[i-1]的值 
	while(j>0 && str[j+1]!=str[i]) {	//注意判断j>0 
		//若第j+1个字符不等于第i个字符 
		//那么j+1不能使前i个字符前后缀相同，应继续循环（重复情况2） 
		j=nxt[j];
	}
	//判断，如果第j+1个字符与第i个字符相同，那么next[i]=j+1 
	if(str[j+1]==str[i])	j++;
	nxt[i]=j;
}

二、求出B在A中的位置

燃鹅仅知道一个字符串的 $n e x t$ 数组是布星的，再回顾问题：
一个文本串A，一个模式串B，A的长度为n，B的长度为m，求B在A中出现的位置。（ $n,m<=10^6$ ）
同样遍历A，假设当前遍历到字符串A的第 $i$ 个字符，且A的前 $i - 1$ 个字符的后 $j$ 个字符与B的前 $j$ 个字符相同。
假设不存在更大的 $j$ ，使得A的后 $j$ 位与B的前 $j$ 位相同。
在这里插入图片描述
如图，若B串的第 $j + 1$ 个字符与A串的第 $i$ 个字符相同，那么现在B就匹配到了第 $j + 1$ 个字符。（不珂能匹配到更多字符，证明过程类似求 $n e x t$ 数组中的情况1，这里不写了）

若第 $j + 1$ 个字符与第 $i$ 个字符不相同，B串就不能匹配 $j + 1$ 位。因此现在需要求出在A串加入第 $i$ 个字符后，B串与A串的后缀最多匹配几位。
首先可以知道能匹配的字符数不会超过 $j + 1$ （证明过程类似求 $n e x t$ 的情况1）。
所以应该把B数组往右移。
在这里插入图片描述
假设移到如图所示的位置时，A串的后 $k$ 位与B串的前 $k$ 位相同。
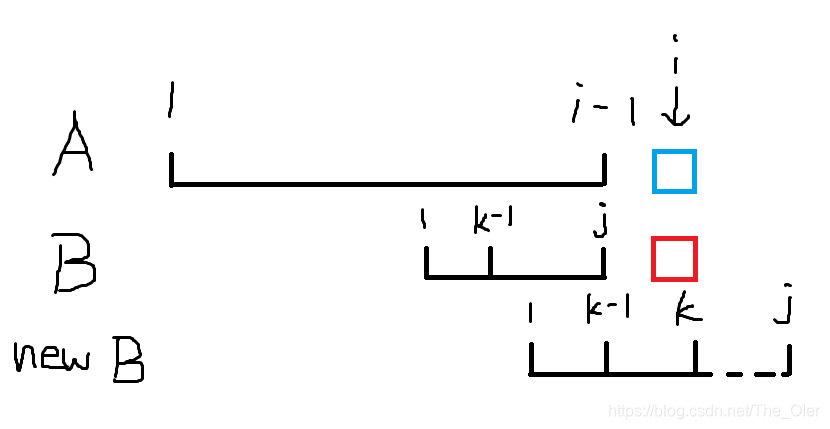
那么我们珂以发现，新的B串（图中的new B）的前 $k - 1$ 个字符，和原B串的前 $j$ 个字符的后 $k - 1$ 个字符重合了。
而因为新的B串和原B串相同，所以B串的前 $j$ 个字符的前 $k - 1$ 个和后 $k - 1$ 个字符相同。
考虑 $n e x t$ 的定义： $n e x t [i]$ 表示前 $i$ 个字符的前后缀相同的最大长度。
因此 $k - 1$ 的最大值为 $n e x t [j]$ ！
但是还需要保证B串的第 $k$ 个字符与A串的第 $i$ 个字符相同。
所以类似求 $n e x t$ 数组的过程，每次让 $j$ 跳到 $n e x t [j]$ 的位置，然后判B串第 $n e x t [j] + 1$ 个字符是否与A串第 $i$ 个字符相等即珂。

代码实现：

for(int i=1; i<=n; i++) {
	//跳到第一个B串的第j+1个字符与A[i]相等的位置（或跳到0，此时表示最大的匹配长度为0） 
	while(j>0 && B[j+1]!=A[i])	j=nxt[j];
	if(B[j+1]==A[i])	j++;
	if(j==m) {
		printf("%d\n",i-m+1);	//输出B在A串中的起始位置 
		j=nxt[j];	//j已经匹配到最后一位，所以重新开始匹配 
	}
}

（可能出现的）疑问

Q：以第二部分求B在A中的位置为例，每次都是把 $j$ 跳到 $n e x t [j]$ 的位置，也就是说， $j$ 会先后变为 $n e x t [j], n e x t [n e x t [j]], . . . . . .$ 那么会不会错过一些本来能使B的前 $j + 1$ 个字符与A的后 $j + 1$ 个字符成立的 $j$ ？
A：不会。错过本来能使B的前 $j + 1$ 个字符与A的后 $j + 1$ 个字符成立的 $j$ ，意味着错过使B前后缀相等的长度 $j$ 。
可以证明， $n e x t [j]$ 是最大的使前 $j$ 个字符前后缀相等的长度， $n e x t [n e x t [j]]$ 是第二大的使前 $j$ 个字符前后缀相等的长度， $n e x t [n e x t [n e x t [j]]$ 是……
过程如下：
由定义， $n e x t [j]$ 是最大的使前 $j$ 个字符前后缀相等的长度，没毛病qwq。
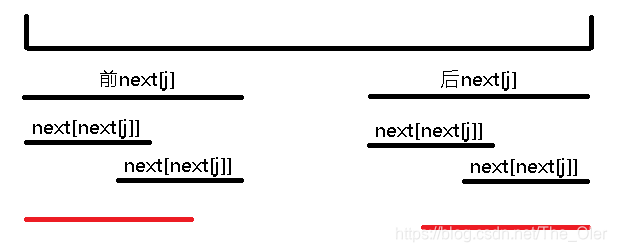
假设第二长的使前 $j$ 个字符前后缀相同的长度不是 $n e x t [n e x t [j]]$ ，而是比 $n e x t [n e x t [j]]$ 长的长度（如图中红线所示）。
在这里插入图片描述
假设红线长度为 $L (L > n e x t [n e x t [j]])$ 。因为红线与前 $n e x t [j]$ 个字符的前 $L$ 个、后 $L$ 个字符均相等，所以 $n e x t [n e x t [j]]$ 应为 $L$ ，矛盾。
所以比 $n e x t [n e x t [j]]$ 大的 $L$ 是不存在的qwq
因此 $n e x t [n e x t [j]]$ 是第二大的使……（不想打了）的长度。
同理 $n e x t [n e x t [n e x t [j]]]$ 是……（懒qwq）
这说明从 $j$ 开始不断取 $n e x t$ 相当于从大到小遍历让前后缀相同的长度，故一定能取到这些长度中最大的一个qwq。

毒瘤代码

//Luogu P3375
#include<stdio.h>
#include<cstring>
#include<algorithm>
#include<math.h>
#define re register int
using namespace std;
typedef long long ll;
int read() {
	re x=0,f=1;
	char ch=getchar();
	while(ch<'0' || ch>'9') {
		if(ch=='-')	f=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9') {
		x=10*x+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int Size=1000005;
int n,m,nxt[Size];
char A[Size],B[Size];
int main() {
	scanf("%s",A+1);
	scanf("%s",B+1);
	n=strlen(A+1);
	m=strlen(B+1);
	int j=0;
	for(re i=2; i<=n; i++) {
		//此时j存储的使next[i-1]的值 
		while(j>0 && B[j+1]!=B[i]) {	//注意判断j>0 
			//若第j+1个字符不等于第i个字符 
			//那么j+1不能使前i个字符前后缀相同，应继续循环（重复情况2） 
			j=nxt[j];
		}
		//判断，如果第j+1个字符与第i个字符相同，那么next[i]=j+1 
		if(B[j+1]==B[i])	j++;
		nxt[i]=j;
	}
	for(re i=1; i<=n; i++) {
		//跳到第一个B串的第j+1个字符与A[i]相等的位置（或跳到0，此时表示最大的匹配长度为0） 
		while(j>0 && B[j+1]!=A[i])	j=nxt[j];
		if(B[j+1]==A[i])	j++;
		if(j==m) {
			printf("%d\n",i-m+1);	//输出B在A串中的起始位置 
			j=nxt[j];	//j已经匹配到最后一位，所以重新开始匹配 
		}
	}
	for(re i=1; i<=m; i++)	printf("%d ",nxt[i]);
	return 0;
}

常用推论

推论1. $n e x t [n e x t [i]]$ 表示第二大的前 $i$ 个字符的前后缀相同的长度， $n e x t [n e x t [n e x t [i]]]$ 表示第三大的使……的长度。
证明：上面已证。

推论2.用若干个串拼在一起（不重叠）把整个字符串覆盖，这样的串的长度最小为 $n - n e x t [n]$ 。
证明：若可以找到更小的长度覆盖整个字符串，则可以证明 $n e x t [n]$ 应该更大。图略。

扩展KMP部分

网上的题解大多是下标从0开始，看着不刁惯并且难受……
推荐一个讲得很好的博客（不过下表是从0开始的）：传送门

给定长度为 $n$ 的串 $S$ ，长度为 $m$ 的串 $T$ ，令 $S [a, b]$ 表示 $S_aS_{a+1}S_{a+2}...S_b$ ， $T [a, b]$ 同理。
令 $e x t e n d [i]$ 表示 $T$ 与 $S [i, n]$ 的最长公共前缀， $n e x t [i]$ 表示 $T$ 与 $T [i, m]$ 的最长公共长度。
（即 $e x t e n d$ 是 $T$ 串与 $S$ 的第 $i$ 位之后的串的最长公共前缀， $n e x t$ 为 $T$ 串与 $T$ 的第 $i$ 位之后的串的最长公共前缀，注意 $n e x t$ 的定义发生了改变）

题外话：为什么这个看起来奇怪的东西叫扩展kmp呢？因为当 $e x t e n d [i] = m$ 时， $T$ 就相当于在 $S$ 中出现了……

规定：
为了方便（和写代码的时候不发生奇怪的变量重名）， $e x t e n d$ 写作 $e x t$ ， $n e x t$ 写作 $n x t$ 。
$S [i]$ 表示 $S$ 的第 $i$ 位， $T [i]$ 同理。

暴莉求 $e x t e n d$ 显然是 $O (n m)$ 的（同 $k m p$ 的暴莉），考虑优化。
假设现在已经求出了 $e x t [1]$ 到 $e x t [i - 1]$ ，现在要求 $e x t [i]$ （先不管 $n x t$ 数组怎么求）。
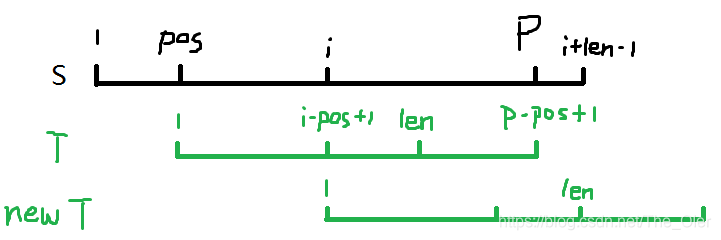
假设之前让 $T$ 与所有的 $S [i, n]$ 匹配时， $S$ 串匹配到的最远位置为 $P$ ，且最远位置是从 $p o s$ 匹配到的。
也就是说， $P = p o s + e x t [p o s] - 1$ ，且 $S [p o s, P] = T [1, P - p o s + 1]$ 。

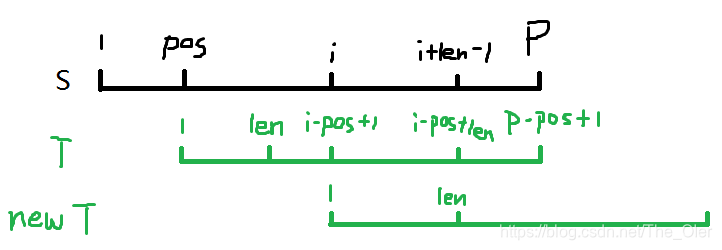
观察此图，发现 $S [i, P] = T [i - p o s + 1, P - p o s + 1]$ 。
而现在我们需要求出 $S [i, n]$ 与 $T [1, m]$ 的最长公共前缀。
根据 $n e x t$ 数组的定义， $n x t [i]$ 表示 $T [i, m]$ 与 $T [1, m]$ 的最长公共前缀。
设 $l e n = n x t [i - p o s + 1]$ ，然后分类讨论：

一、 $\small i+len-1<=P$

$l e n = n x t [i - p o s + 1]$ 表示 $T [1, l e n] = T [i - p o s + 1, i - p o s + l e n]$ ，因为 $i + l e n - 1$ 在 $P$ 左边。
那么 $i + l e n - 1 < = P$ 表示 $S$ 串中 $S [i, i + l e n - 1] = T [i - p o s + 1, i - p o s + l e n] = T [1, l e n]$ （如图）。
在这里插入图片描述
此时 $e x t [i] = l e n$ ，因为
（1） $S [i, i + l e n - 1] = T [1, l e n]$
（2）若 $e x t [i] > l e n$ ，则说明 $T [l e n + 1] = T [i - p o s + l e n + 1]$ ，则 $n x t [i - p o s + 1] > l e n$ ，与 $n x t$ 的定义不符。
因此 $e x t [i] = l e n$ 。

二、 $\small i+len-1>P$

在这里插入图片描述
如图， $S [P + 1, i + l e n - 1]$ 是一段没有比较过的位置，无法确定与 $T$ 是否相等。
而 $S [i, P] = T [1, P - i + 1]$ ，所以从 $S$ 的第 $P + 1$ 位， $T$ 的第 $P - i + 2$ 位开始暴力匹配，失配时表示这个长度是 $e x t [i]$ 的值。

讲到这里，读者应该能写出求解 $e x t$ 数组的方法。
我的代码写得比较毒瘤，仅供参考qwq

void GetExtend() {
	int j=1;
	while(j<=n && j<=m && s[j]==t[j])	j++;
	ext[1]=j-1;
	int pos=1;
	for(re i=2; i<=n; i++) {
		//这个地方比较玄学，不能写i+nxt[i-pos+1]-1<=pos+ext[pos]-1
		if(i+nxt[i-pos+1]<=pos+ext[pos]-1) {
			ext[i]=nxt[i-pos+1];
		} else {
			j=max(pos+ext[pos],i);
			while(j<=n && j-i+1<=m && s[j]==t[j-i+1]) {
				j++;
			}
			ext[i]=j-i;
			pos=i;
		}
	}
}

求解 $n x t$ 数组的方法比较类似。因为 $n x t [i]$ 表示的是 $T [i, m]$ 与 $T$ 的最长公共前缀，而 $e x t [i]$ 表示的是 $S [i, m]$ 与 $T$ 的最长公共前缀，所以求 $n x t$ 时就让 $T$ 和 $T$ 本身执行求 $e x t$ 的过程即珂。
由于求 $n x t [i]$ 过程中，需要用到的 $n x t$ 的下标都比 $i$ 小，所以不会出现调用没有被求出的 $n x t$ 值。

void GetNext() {
	nxt[1]=m;
	int j=1;
	while(j<m && t[j]==t[j+1])	j++;
	nxt[2]=j-1;
	int pos=2;
	for(re i=3; i<=m; i++) {
		if(i+nxt[i-pos+1]<=pos+nxt[pos]-1) {
			nxt[i]=nxt[i-pos+1];
		} else {
			j=max(pos+nxt[pos],i);
			while(j<=m && t[j]==t[j-i+1]) {
				j++;
			}
			nxt[i]=j-i;
			pos=i;
		}
	}
}

毒瘤代码

输出 $e x t e n d$ 数组：

#include<stdio.h>
#include<cstring>
#include<algorithm>
#include<math.h>
#define re register int
using namespace std;
typedef long long ll;
int read() {
	re x=0,f=1;
	char ch=getchar();
	while(ch<'0' || ch>'9') {
		if(ch=='-')	f=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9') {
		x=10*x+ch-'0';
		ch=getchar();
	}
	return x*f;
}
const int Size=100005;
int n,m,nxt[Size],ext[Size];
char s[Size],t[Size];
void GetNext() {
	nxt[1]=m;
	int j=1;
	while(j<m && t[j]==t[j+1])	j++;
	nxt[2]=j-1;
	int pos=2;
	for(re i=3; i<=m; i++) {
		if(i+nxt[i-pos+1]<=pos+nxt[pos]-1) {
			nxt[i]=nxt[i-pos+1];
		} else {
			j=max(pos+nxt[pos],i);
			while(j<=m && t[j]==t[j-i+1]) {
				j++;
			}
			nxt[i]=j-i;
			pos=i;
		}
	}
}
void GetExtend() {
	int j=1;
	while(j<=n && j<=m && s[j]==t[j])	j++;
	ext[1]=j-1;
	int pos=1;
	for(re i=2; i<=n; i++) {
		if(i+nxt[i-pos+1]<=pos+ext[pos]-1) {
			ext[i]=nxt[i-pos+1];
		} else {
			j=max(pos+ext[pos],i);
			while(j<=n && j-i+1<=m && s[j]==t[j-i+1]) {
				j++;
			}
			ext[i]=j-i;
			pos=i;
		}
	}
}
int main() {
//	freopen("data.txt","r",stdin);
//	freopen("WA.txt","w",stdout);
	scanf("%s",s+1);
	scanf("%s",t+1);
	n=strlen(s+1);
	m=strlen(t+1);
	GetNext();
	GetExtend();
	for(re i=1; i<=n; i++) {
		printf("%d ",ext[i]);
	}
	return 0;
}
/*
dadab
dad
*/

例题

还没写题，待续qwq

ILoveFujibayashiRyou

关注

3
点赞
踩
3

收藏

觉得还不错? 一键收藏
0
评论
KMP&扩展KMP学习笔记（多图预警）

例子：一个文本串A，一个模式串B，A的长度为n，B的长度为m，求B在A中出现的位置。（n,m<=106n,m<=10^6n,m<=106）暴力：枚举文本串中的位置iii，暴力比较A的[i,i+m−1][i,i+m-1][i,i+m−1]这个区间是否与B相同。时间复杂度最坏情况是A，B都只有一种字符（比如A是aaaaa，B是aaa），此时时间复杂度为O(nm)O(nm)O(nm)...
复制链接

扫一扫