可视化红黑树详解（gif图演示，洛谷P3369 普通平衡树）

已于 2024-04-02 22:15:40 修改
阅读量1k 收藏 18
点赞数 33
文章标签： 红黑树 数据结构 平衡树
于 2024-04-02 21:53:41 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/the_oier/article/details/137172427
版权

文章目录

写在前面

推荐一个很实用的工具：红黑树可视化

本文参考OI wiki中的红黑树代码，读者也可以参考该篇解析（写得还是很不错的），不过OI Wiki里删除后平衡维护的Case 4和Case 5在代码细节上稍微有些问题（把 c c c, d d d 均为红色算进Case 4了，这样不会出bug，只是相当于绕了个弯）。

大部分红黑树代码都采用 rotateLeft 和 rotateRight 两个函数来进行旋转，而且在找close/distant nephew的时候也是分类讨论，这样比较麻烦。
我们其实可以使用 node *ch[2] 来表示左右孩子，ch[0] 表示左孩子，ch[1] 表示右孩子。在后续使用中，我们#define left ch[0], #define right ch[1]，从而兼容用 left, right 找左右孩子的方法。这种存储方式的好处是，我们可以通过异或1来轻松切换左右分支，而不是采用三目运算符来找兄弟节点。
再考虑 rotate，其实 rotate 相当于把某个子节点往上转到其父节点的位置，因此我们可以用同一个 rotate 函数来表示左旋或右旋，使用时旋转左孩子即为 rotateLeft，旋转右孩子即为 rotateRight。

红黑树是什么

如果能把一个又一个节点积累起来，也许就能变成一棵红黑树。 ——高松灯

红黑树是一棵满足特殊性质的二叉搜索树。它的特殊性质有：

  1. 节点均为红色/黑色（顾名思义）
  2. NIL 节点（空叶子节点，有时也叫外部节点）为黑色
  3. 红色节点的子节点均为黑色
  4. 从根节点（不含根节点本身）到 NIL 节点的每条路径上的黑色节点数量相同

（注：有的教材/解析要求根节点一定是黑色，不过这个没有太大影响，根节点是红色也不会影响树的平衡性）

我们把第 4 条性质中，从某节点出发（不含节点本身），到任意 NIL 节点路径上的黑节点数，称为节点的“黑高”（black height）。
这里黑高的定义是比较反直觉的（究竟是谁定义的？），因为既要去掉节点本身，又要加上一个额外的 NIL 节点。
可以用以下递推式来加深对黑高的理解：
b h [ N I L ] = 0 bh[NIL] = 0 bh[NIL]=0
∀ s ∈ s o n ( x ) , \forall s \in son(x), ∀s∈son(x), b h [ x ] = b h [ s ] + [ c o l o r ( s ) = = B L A C K ] bh[x] = bh[s] + [color(s) == BLACK] bh[x]=bh[s]+[color(s)==BLACK]，中括号表示该表达式的bool值，若表达式成立则为1，表达式不成立则为0.

我们把粉色头发的ano酱作为红节点，黑色头发的Rikki作为黑节点，那么下面这棵树是一棵红黑树：
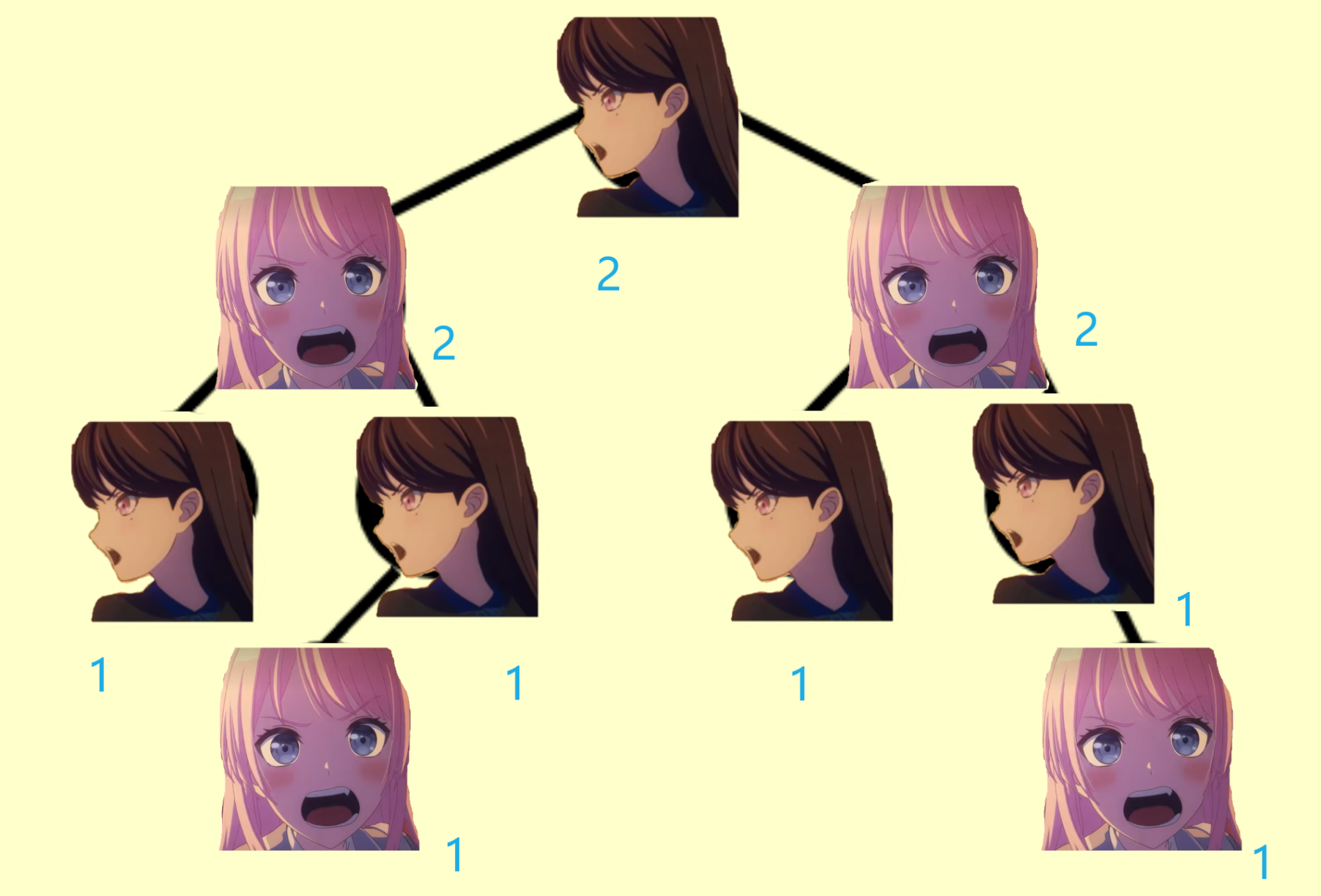
在这里插入图片描述

其中蓝色数字标注的是节点的黑高。
假如给上面这棵树的节点填入权值，就是一棵标准的红黑树：
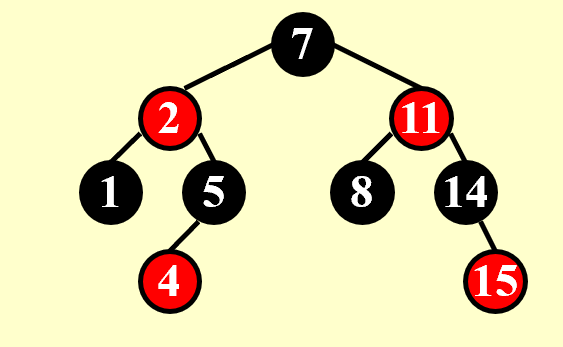
在这里插入图片描述

红黑树的平衡性

考虑这样一个问题：一棵“黑高”为 h h h的红黑树，至少会有多少节点？（“黑高”是指根到任意NIL节点路径上的黑节点数）
其实可以用归纳法证明结果是 2 h − 1 2^h-1 2h−1，这里提供另一种思路：

对于黑高确定的红黑树，我们要想节点数最少，直接全部放黑节点就可以了。因为往里面放红节点不会对黑高产生任何影响，而且由于红节点的子节点必须是黑节点，放红节点还会让总节点数变得更多。
而全为黑节点的红黑树必然是一棵满二叉树，因为根节点到任意NIL节点路径上的黑节点数相同，如果某个部分缺了一块，那这部分的黑高就会减少。
那么，黑高为 h h h的红黑树，节点最少的情况是一棵高为 h h h，全是黑节点的满二叉树（注意高是 h h h而不是 h + 1 h+1 h+1，因为计算黑高时多统计了一次NIL节点，又少统计一次自身，二者抵消了）。这样的树有 2 h − 1 2^h-1 2h−1个节点。
因此，一棵“黑高”为 h h h的红黑树，至少有 2 h − 1 2^h-1 2h−1个节点。（ N = s i z e o f ( x ) ≥ 2 b h ( x ) − 1 N = \rm sizeof(x)\ge 2^{bh(x)}-1 N=sizeof(x)≥2bh(x)−1）

我们还知道，红节点的两个孩子一定为黑节点，所以说，根节点到NIL节点的路径上，一个红节点就必定有一个黑节点与之对应，所以红节点数一定不超过黑节点数。
因此， b h ( T r e e ) ≥ h ( T r e e ) / 2 \rm bh(Tree)\ge h(Tree)/2 bh(Tree)≥h(Tree)/2。

根据上面两个不等式，可以推出：

一棵有 N N N个节点的红黑树，树高不超过 2 log ⁡ ( N + 1 ) 2\log (N+1) 2log(N+1)。

也就是说，红黑树天生就是平衡的，树高在 O ( log ⁡ N ) O(\log N) O(logN)级别。
假如我们能在插入和删除时维护好红黑树的几条性质，我们就能得到一棵高恒为 O ( log ⁡ N ) O(\log N) O(logN)的二叉搜索树。

红黑树整体框架

红黑树类定义为：

template<typename T>
class RedBlackTree {
	private:
		struct node;
		node* root;		//根节点
		//...
	public:
		int size();
		void insert(T);
		bool remove(T);
		//...
};

节点定义为：

#define RED 1
#define BLACK 0
#define left ch[0]
#define right ch[1] 
template<typename T>
struct RedBlackTree<T>::node {
	T val;			//权值
	bool color;		//1 is red, 0 is black 
	node *father, *ch[2];
	int siz;		//子树大小
	int direction() {
		if(father == NULL)	return 0;
		return father->right == this;
	}
	node* sibling() {
		if(father == NULL)	return NULL;
		return father->ch[direction() ^ 1];
	}
	node* uncle() {
		if(father == NULL)	return NULL;
		return father->sibling();
	}
	void pushup() {
		siz = (left?left->siz:0) + (right?right->siz:0) + 1;
	}
	//......
}

其中val代表节点权值，siz代表子树大小，ch[0] 和 ch[1] 分别代表左右孩子。
direction() 表示当前节点所在分支（0为左孩子，1为右孩子），sibling(), uncle() 是在插入/删除中需要经常用到的亲戚节点。为了方便，我们统一提前写好。

旋转操作

可以参考splay树的旋转操作。这里我们不需要区分左旋和右旋，rotate(x) 表示把节点 x x x 旋转到它父亲的位置。

template<typename T>
void RedBlackTree<T>::connect(node *x, node *fa, int k) {
	if(x != NULL)	x->father = fa;
	if(fa != NULL) {
		fa->ch[k] = x;
	} else {
		root = x;
	}
}

template<typename T>
void RedBlackTree<T>::rotate(node *x) {
	//rotate x to its parent's position
	node* y = x->father;
	node* z = y->father;
	int yson = x->direction();	//the branch of x, 0 is left, 1 is right
	if(z == NULL) {
		root = x;
		x->father = NULL;
	} else {
		int zson = y->direction();
		connect(x, z, zson);
	}
	connect(x->ch[yson^1], y, yson);
	connect(y, x, yson^1);
	y->pushup();
	x->pushup();
}

插入操作

从今天开始，我们就是一起演奏音乐的命运共同体！ ——丰川祥子

红黑树的插入与普通的 BST 的插入操作类似。
我们将新节点作为红节点插入到树中对应位置，再根据相关节点状态进行调整，使整棵树满足红黑树的性质。
具体地说，红黑树要求红节点的子节点均为黑节点，而插入一个红节点可能会使父节点和子节点均为红色，所以在插入后，我们需要进行双红修正。
插入操作的代码实现如下：

template<typename T>
void RedBlackTree<T>::insert(T v) {
	node *x = root, *fa = NULL;
	while(x != NULL) {
		x->siz++;
		fa = x;
		if(v < x->val) {
			x = x->left;
		} else {
			x = x->right;
		}
	}
	x = new node(v, RED, fa);	//create a new node
	if(fa == NULL) {
		root = x;
	} else if(v < fa->val) {
		fa->left = x;
	} else {
		fa->right = x;
	}
	SolveDoubleRed(x);
}

双红修正

不过，为了下次不失败而努力不就好了？就算失败一次，也要有重来的信心。 ——千早爱音

上面的插入过程中，可能会出现父节点和子节点都是红色的连续双红情况，这违反了红黑树的性质。
在 SolveDoubleRed(x) 函数中， x x x 为红节点，我们检查 x x x 的父节点是否为红节点，如果是，则进行修正。（也就是说，这里 x x x 表示连续双红节点的子节点）
修正时，我们要保证红黑树的性质成立，即不出现连续的双红节点，以及保证黑高相同。

在下面的所有注释中，我们用<X>来表示红节点，[X]表示黑节点，{X}表示任意颜色的节点。

Case 1, 2

x x x 为根（父节点为空），或 x x x 的父节点为黑，此时无需修正。下面都是需要修正的情况。

Case 3

x x x 的父节点 p p p 为根节点，此时把 p p p 染黑即可。

if(p == root) {
	// Case 3: Parent is root and is RED
	//   Paint parent to BLACK.
	//    <P>         [P]
	//     |   ====>   |
	//    <X>         <X>
	p->color = BLACK;
	return;
}

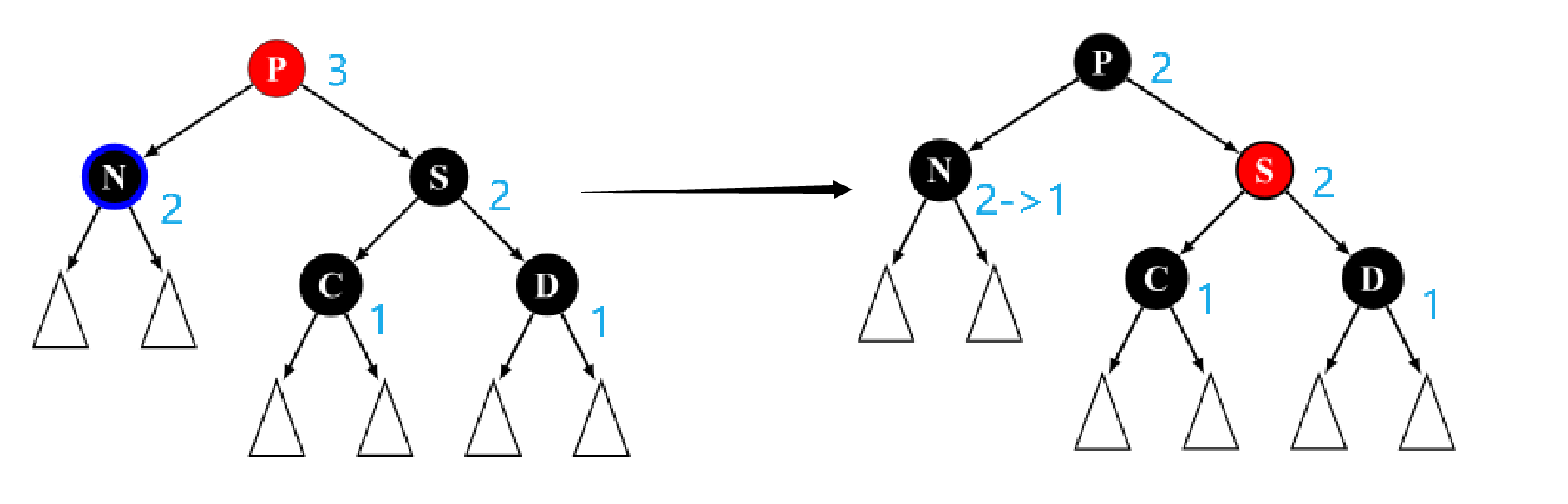
Case 4

x x x （图中的 N）的父节点 p p p，叔节点 u u u 均为红色。由于该树原本是一棵合法的红黑树，所以 x x x 的祖父节点 g g g 一定是黑色。
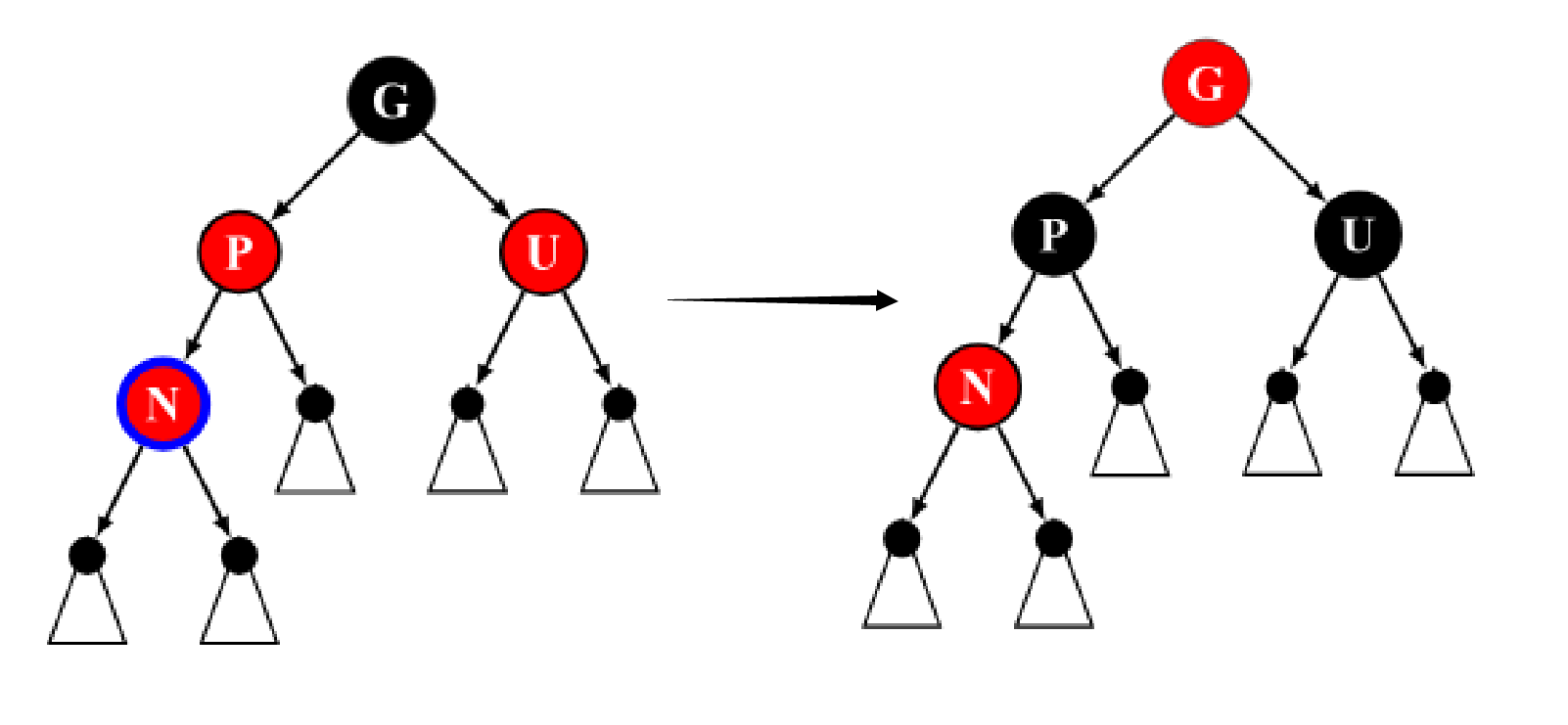
在这里插入图片描述

此时我们将 p p p 和 u u u 染黑，将 g g g 染红，这样在 g g g 以下就不会有连续的红节点。
由于插入前 g g g 到 NIL 节点经历的黑节点数都相同，所以把 p p p, u u u 都染黑后黑节点数仍然相同。且因为又把 g g g 染为了红色，所以不会对 g g g 往上的节点的黑高产生影响。
不过这时节点 g g g 与 g g g 的父亲又有可能是连续的红节点，因此我们递归对 g g g 进行双红修正。
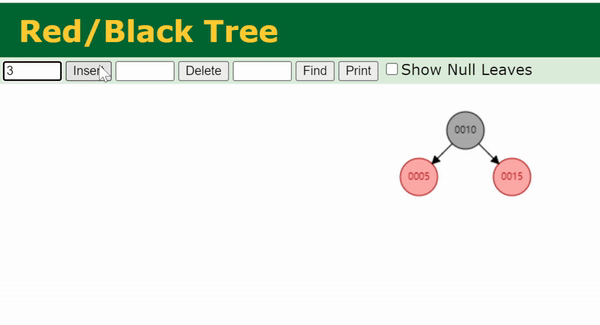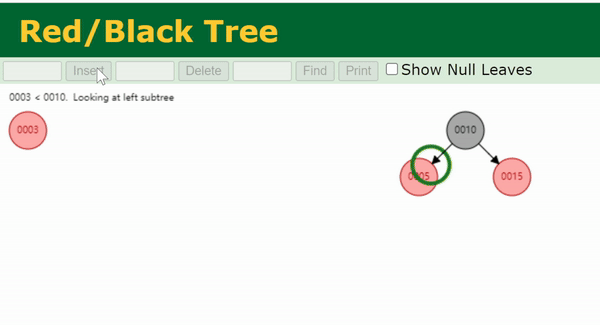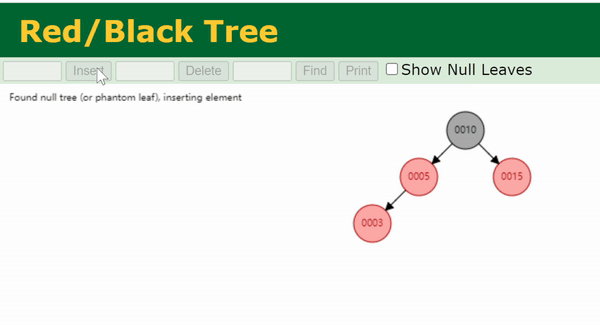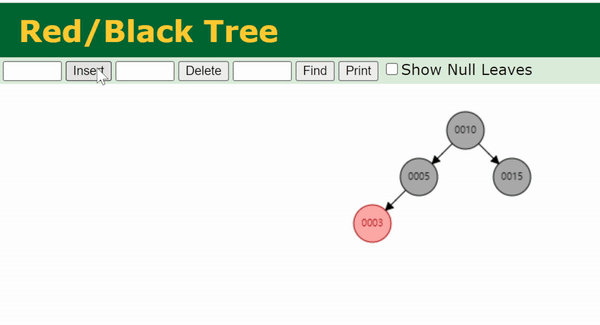
请添加图片描述

if(x->hasUncle() && x->uncle()->color == RED) {
	// Case 4: Both parent and uncle are RED
	//   Paint parent and uncle to BLACK;
	//   Paint grandparent to RED;
	//   Maintain grandparent recursively.
	//        [G]             <G>
	//        / \             / \
	//      <P> <U>  ====>  [P] [U]
	//      /               /
	//    <X>             <X>
	p->color = BLACK;			//parent -> black
	x->uncle()->color = BLACK;	//uncle  -> black
	p->father->color = RED;		//grandparent -> red
	SolveDoubleRed(p->father);
	return;
}

Case 5

叔节点为黑色，且当前节点 x x x 与父节点 p p p 的方向相反（即一个为左子节点，一个为右子节点）。
这种情况无法直接维护，我们把节点 x x x 旋转上来，然后就转化为了Case 6。
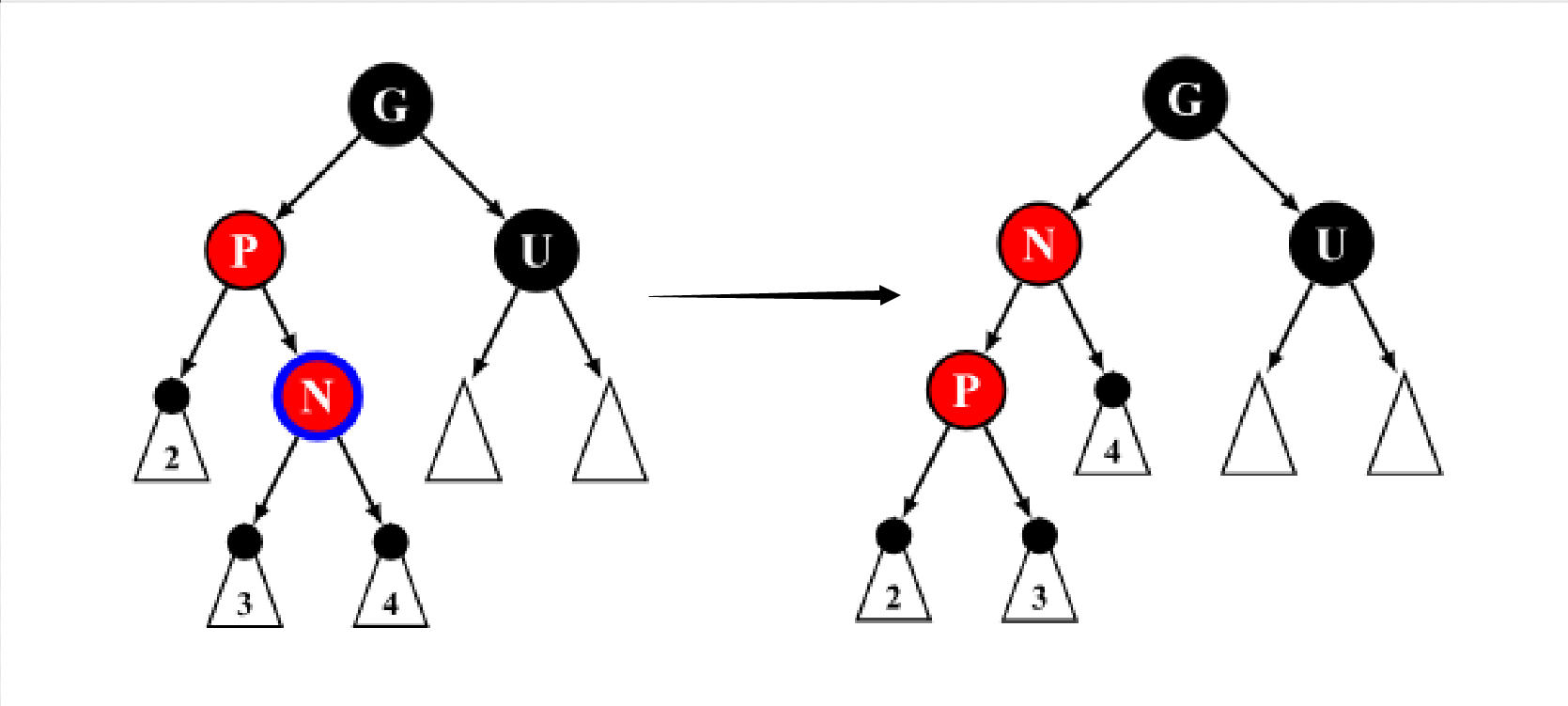
在这里插入图片描述
把 x x x 转上来后， x x x 与 p p p 的方向就一致了，这时 p p p 成为了 x x x 的父节点，于是我们需要处理的节点变成了 p p p。
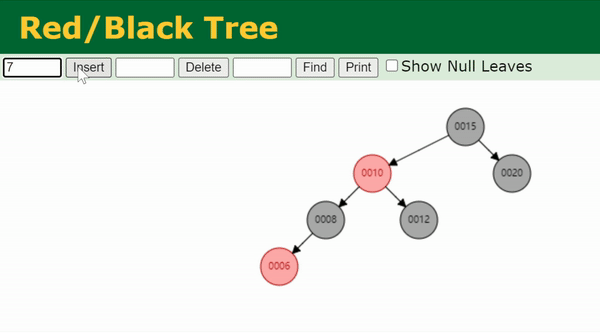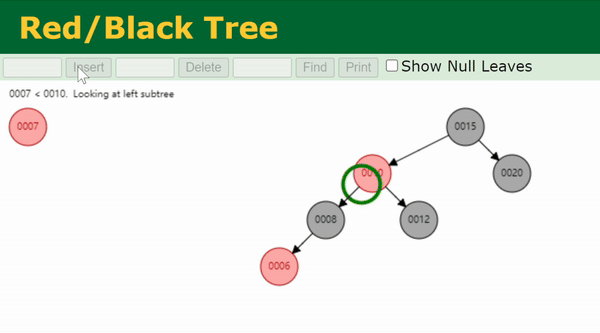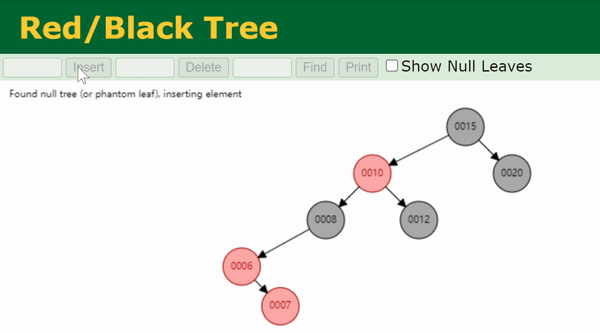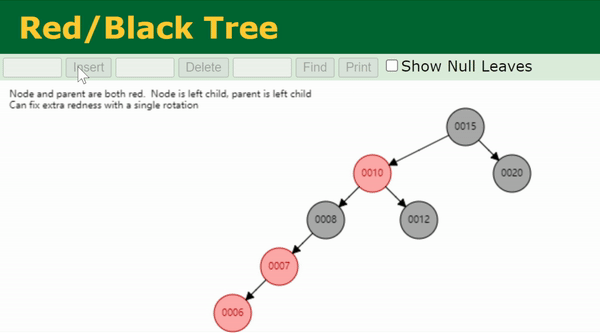
请添加图片描述

// Case 5 & 6: parent is RED, uncle is BLACK(or NULL)
if(x->direction() != p->direction()) {
	// Case 5: Current node is the opposite direction as parent
	//   Step 1. Rotate x to parent's position.
	//   Step 2. Goto Case 6.
	//      [G]                 [G]
	//      / \    rotate(X)    / \
	//    <P> [U]  ========>  <X> [U]
	//      \                 /
	//      <X>             <P>
	rotate(x);
	x = p;			//Now P is the child of double red.
	p = x->father;	//reset p to x's father
}

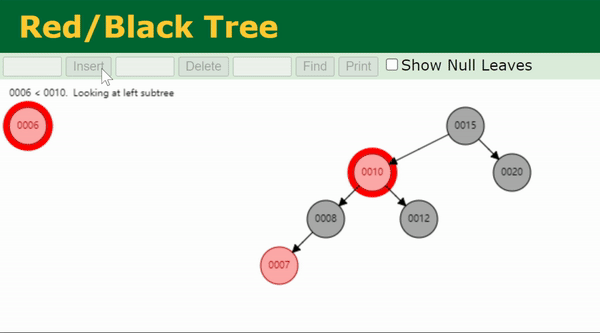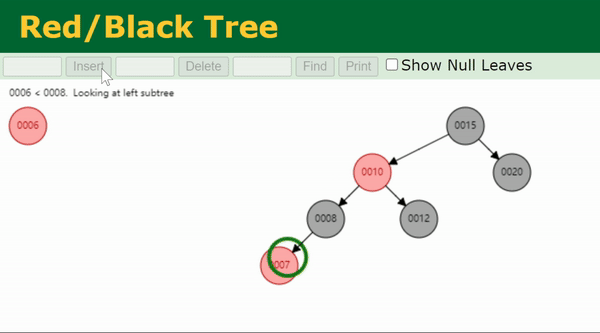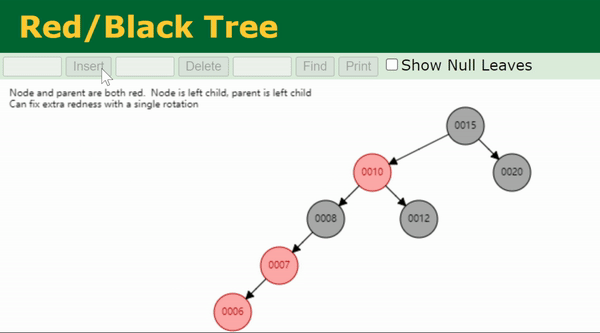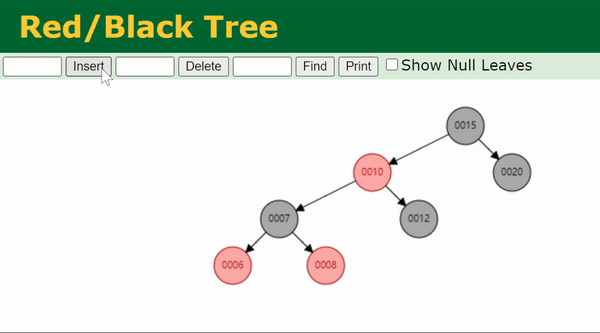
Case 6

叔节点为黑色，且当前节点 x x x 与父节点 p p p 的方向相同（即同为左子节点或右子节点）。
由于父节点 p p p 是红色，所以祖父节点 g g g 一定是黑色。这种情况下，我们先向上转一次 p p p，再把 p p p 染黑， g g g 染红。
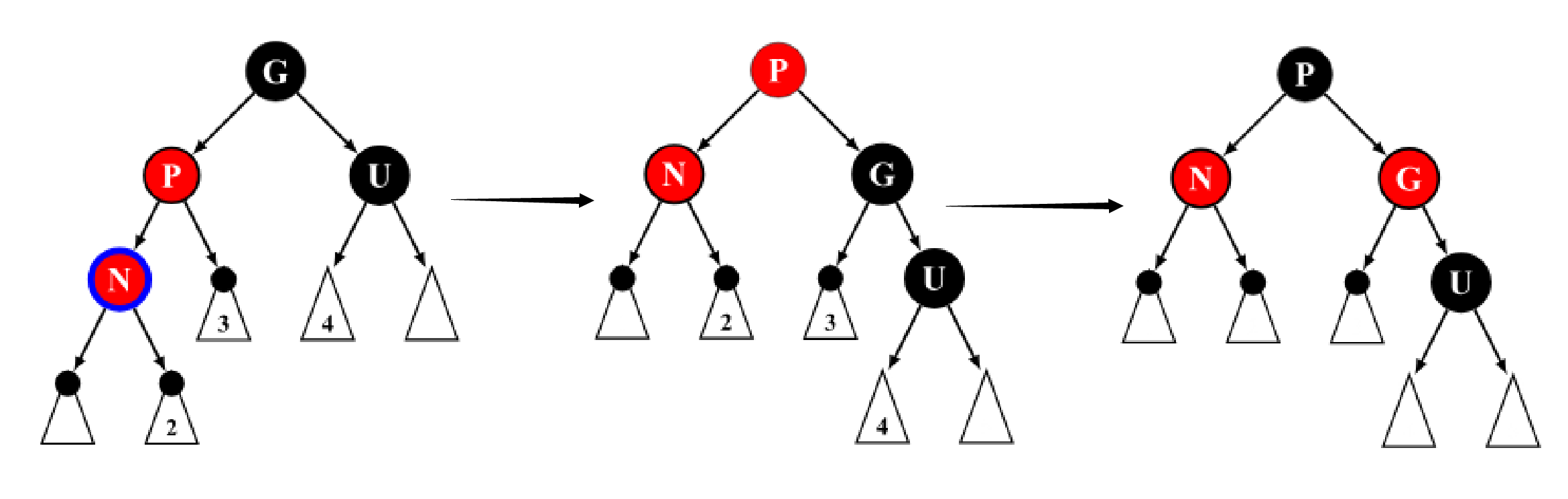
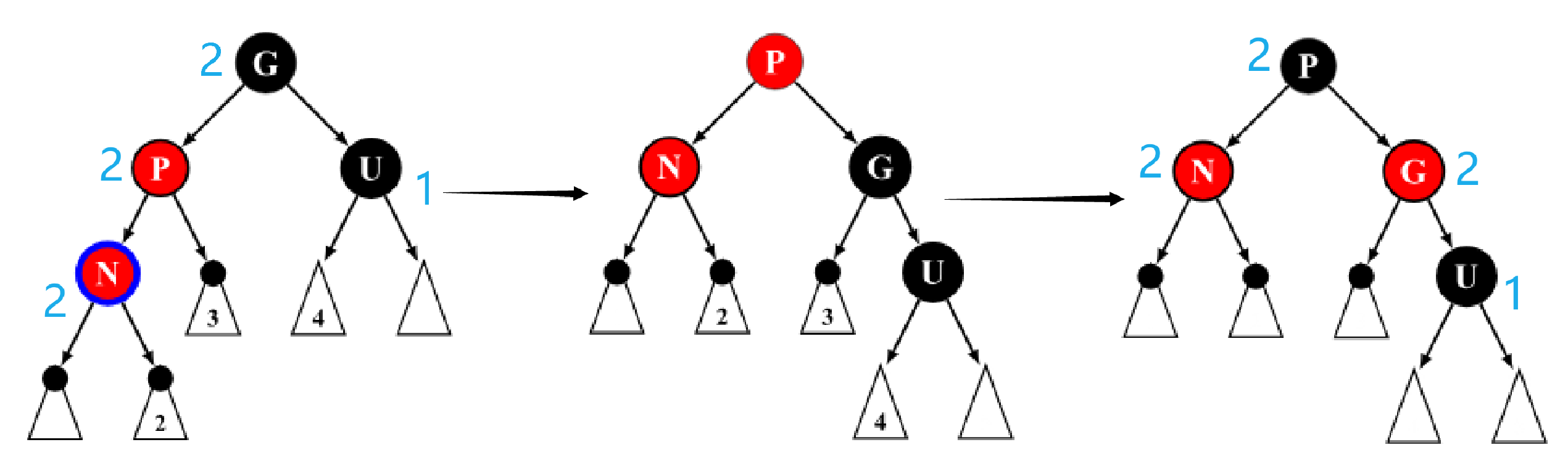
在这里插入图片描述
这里可以证明，这样操作后，树的黑高是不变的。我们假设最左边的图中 u u u 的黑高是1（即两个子节点均为 NIL），那么 g g g 的黑高是2，则由于黑高相同的性质， p p p 和 x x x（图中的N）黑高也为2.
在旋转+重新染色后， x x x 和 u u u 的子树结构和颜色没有变化，因此 x x x 的黑高仍为2， u u u 的黑高仍为1. 那么 g g g 的黑高为2， p p p 的黑高为2，与开始时 g g g 的黑高一致。
在这里插入图片描述
请添加图片描述

	// Case 6: Current node is the same direction as parent
	//   Step 1. Rotate parent to grandparent's position
	//   Step 2. Paint parent (before rotate) to BLACK;
	//           Paint grandparent (before rotate) to RED.
	//        [G]                 <P>               [P]
	//        / \    rotate(P)    / \    repaint    / \
	//      <P> [U]  ========>  <X> [G]  ======>  <X> <G>
	//      /                         \                 \
	//    <X>                         [U]               [U]
	rotate(p);				//rotate x's parent
	p->color = BLACK;
	x->sibling()->color = RED;	//repaint

删除操作

这个，不需要了！ ——长崎素世

二叉查找树

我们先考虑单纯的二叉搜索树怎么删除一个节点。
根据要删除的节点的子节点数，可以分为三种情况：0个子节点（即叶节点），1个子节点（一条链的正中间），以及2个子节点（内部节点）。

删除叶节点是最简单的，直接把这个节点去掉就行了。
如果是1个子节点的情况，就与链表的删除比较类似，我们用这个子节点来代替原来被删除的节点。
2个子节点的情况，我们找到删除节点的后继节点，也就是右子树中权值最小的节点。找后继节点的方法是从右子节点开始一直往左走，直到没有左子节点为止。
（后继节点一定没有左子节点，也就是说，它只有0或1个子节点）
由于后继节点是原来右子树中最小的节点，所以把它原来的权值放到被删除节点的位置，仍然满足左子树 < 根 < 右子树的性质。
因此，我们交换删除节点和后继节点的权值，然后把后继节点删除，这就转化成了对有0或1个子节点的节点进行删除的情况。

红黑树

考虑删除有0或1个子节点的节点的情况。（有2个子节点的情况是可以转化成这两种情况的，所以不用讨论）
删除有1个子节点的节点时，是用它唯一的子节点代替本身。删除叶节点（0个子节点）时，可以看作用一个 NIL 节点代替它本身。
我们再考虑红黑树关键的两条性质：不能出现连续双红节点，以及黑高相同。
假如我们删除的是红节点，那么它的替代节点一定是黑节点，所以删除它既不会使树中出现双红节点，也不会影响黑高相同的性质。
但是如果删除的是黑节点，那么会使经过这个节点的路径的黑高-1，而且如果父节点、子节点都是红色，就会出现连续的双红了。
这里双红是很容易处理的，我们的重点在于处理黑高（“双黑”）。如果我们可以简单通过重新染色解决黑高不同的问题，那就简单处理就好了。但是有的时候这样行不通，我们就需要进行双黑修正。
具体地说，我们需要调整树的结构和颜色，把目标黑色节点放在一个比兄弟节点黑高多1的位置，再把目标节点删掉，这样黑高就相同了。

template<typename T>
bool RedBlackTree<T>::remove(T v, node* x) {
	if(x == NULL)	return false;
	if(v != x->val) {
		int branch = (v > x->val);	//v > x->val : branch = 1, goto right child
		if(x->ch[branch] != NULL) {
			//the structure of the subtree may change
			//node x may have new children after remove
			//so first update the size of subtree
			//if fail to remove then rollback size changes
			x->siz--;
			bool result = remove(v, x->ch[branch]);
			if(result == false) {
				x->siz++;
			}
			return result;
		}
		return false;
	}
	//Remove x from the tree
	//......
}

Case 0

删除节点为根，且整棵树只有这一个节点，直接删就完了。

Case 1

删除节点 x x x 有2个子节点，则交换当前节点与后继节点的权值，然后问题转化为删除后继节点。

if(x->left != NULL && x->right != NULL) {
	// Case 1: If the node is strictly internal
	//   Step 1. Find the successor S with the smallest key
	//           and its parent P on the right subtree.
	//   Step 2. Swap the data (key and value) of S and X,
	//           S is the node that will be deleted in place of X.
	//   Step 3. X = S, goto Case 2, 3
	//     |                    |
	//     X                    S
	//    / \                  / \
	//   L  ..   swap(X, S)   L  ..
	//       |   =========>       |
	//       P                    P
	//      / \                  / \
	//     S  ..                X  ..
	x->siz--;
	//Step 1
	node* rt = x->right;
	rt->siz--;
	while(rt->left) {
		rt = rt->left;
		rt->siz--;
	}
	//Step 2, 3
	node* succ = rt;
	swap(x->val, succ->val);
	x = succ;
}

Case 2

删除叶子节点。如果是红叶子就直接删掉，如果是黑叶子，就要重新维护黑高。
在维护操作中，由于我们只是把目标节点放到了比兄弟节点黑高多1的地方，而没有改变目标节点的子树结构和数据，所以我们可以先对其维护，让它的黑高比兄弟多1，再把它删除。

if(x->left == NULL && x->right == NULL) {
	// Case 2: Current node is a leaf
	//   Step 1. Put X to a position where its black height
	//           is greater than its sibling by 1.(if X is black)
	//   Step 2. remove X

	// The maintain operation won't change the node itself,
	//  so we can perform maintain operation before unlink the node.
	x->siz = 0;
	if(x->color == BLACK) {
		SolveDoubleBlack(x);	//Step 1
	}
	x->father->ch[x->direction()] = NULL;
	x->father->pushup();
	return true;
}

Case 3

目标节点刚好有一个子节点，我们用它唯一的子节点来代替它本身。
这时唯一的孩子只可能是红色，否则一边为黑，一边为NIL，两边的黑高是不同的。
因此，我们直接把替代节点染成黑色，就可以解决黑高-1的问题。

	// Case 3: Current node has a single left or right child
	//   Step 1. Paint its child to black(the child must be red).
	//   Step 2. Remove X
	node* replacement = (x->left != NULL ? x->left : x->right);
	if(x->color == BLACK) {
		replacement->color = BLACK;
	}
	if(x == root) {
		root = replacement;
		replacement->father = NULL;
	} else {
		node* parent = x->father;
		parent->ch[x->direction()] = replacement;
		replacement->father = parent;
		parent->pushup();
	}

OI Wiki上这一段代码和最后给出的完整版里不一样，最后的完整版还写了唯一孩子是黑色时维护孩子的 if 分支，这个可能是出于工程上代码完整性的考虑（？

双黑修正

致命的黑影啊，翩翩起舞吧！ ——Ave Mujica《黑色生日》

双黑维护，其实就是目标节点的黑高因为某些情况（如删除了一个黑节点）减少了1（或者即将要减少1），导致它比兄弟节点的黑高少1.
我们需要把它放在一个比兄弟黑高多1的位置，从而抵消黑高-1的影响。

Case 1

兄弟节点 s s s 为红色，则父节点 p p p 和两个侄节点 c c c 和 d d d 必为黑色。这种情况与双红修正的Case 5类似，无法直接使其满足所有性质，我们将其转化为其他Case进行处理。
Step 1. 往上转一次兄弟节点 s s s
Step 2. 把 s s s 染黑， p p p 染红，并转到其他Case
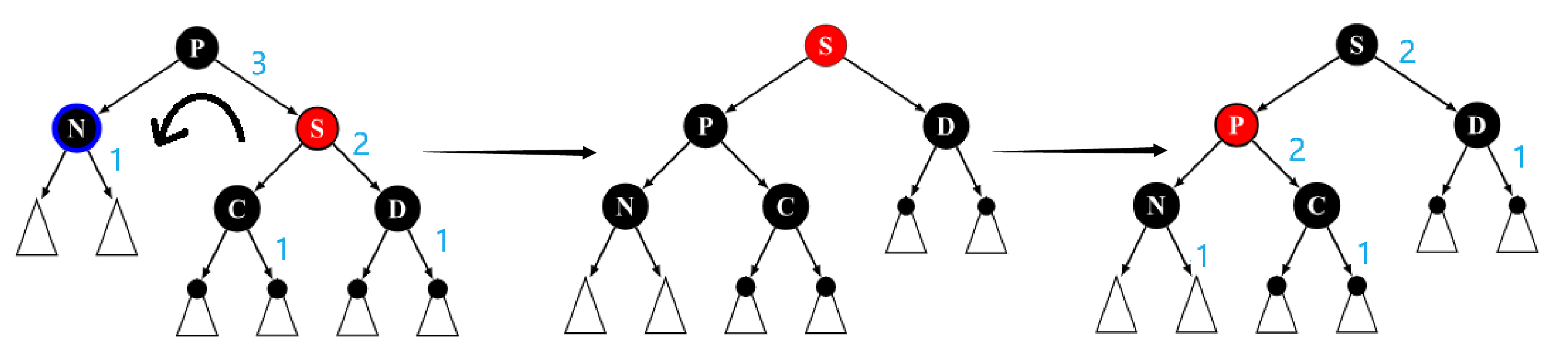
在这里插入图片描述
假设原来黑高为上面最左边蓝色数字标注的值，则这样操作后目标节点与新的兄弟节点 c c c 黑高相同。由于我们需要目标节点比兄弟黑高多1，所以我们转到其它Case，继续对该节点进行处理。
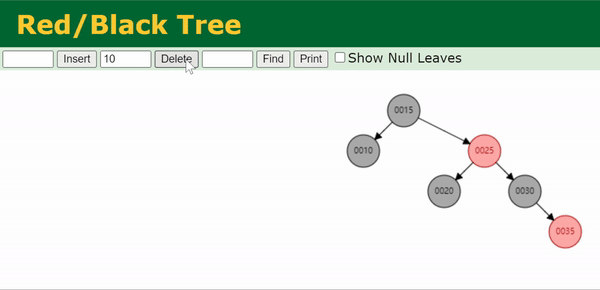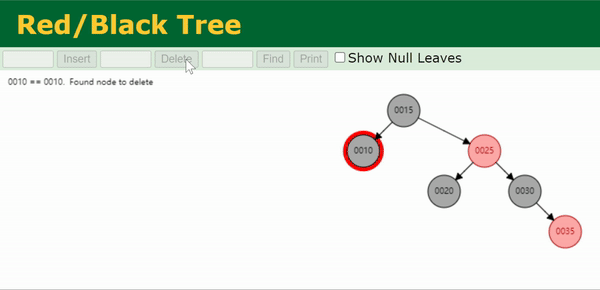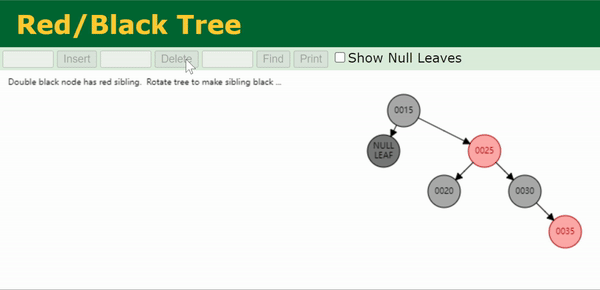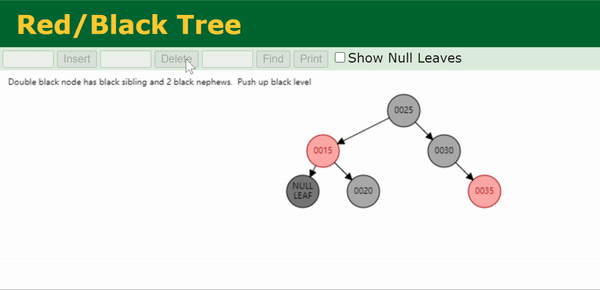
请添加图片描述

if(sibling->color == RED) {
	// Case 1: Sibling is RED, parent and nephews must be BLACK
	//   Step 1. Rotate X's sibling to P's position
	//   Step 2. Paint S to BLACK, P to RED
	//   Step 3. Goto Case 2, 3, 4, 5
	//      [P]                   <S>               [S]
	//      / \     rotate(S)     / \    repaint    / \
	//    [X] <S>  ==========>  [P] [D]  ======>  <P> [D]
	//        / \               / \               / \
	//      [C] [D]           [X] [C]           [X] [C]
	node* parent = x->father;
	//Step 1
	rotate(sibling);
	//Step 2
	sibling->color = BLACK;
	parent->color = RED;
	sibling = x->sibling();		//update sibling after rotation
}

Case 2

兄弟节点 s s s 和侄节点 c c c, d d d 均为黑色，且父节点 p p p 为红色。
此时将父节点 p p p 染红，将 s s s 染黑即可。
在这里插入图片描述

假设原来的黑高如左图所示，那么重新染色之后，再删除目标节点，则其替代节点的黑高由2变为1。删除后， p p p 的黑高为2。
假如 p p p 有一个父节点，则原来 p p p 的父节点黑高为3（因为原来 p p p 是红色），调整后父节点黑高也为3（ p p p 为黑，父节点黑高为 p p p 的黑高+1）.
请添加图片描述

bool closeBlack = (closeNephew == NULL) || (closeNephew->color == BLACK);
bool distantBlack = (distantNephew == NULL) || (distantNephew->color == BLACK);
if(closeBlack && distantBlack) {
	if(x->father->color == RED) {
		// Case 2: Sibling and nephews are BLACK, parent is RED
		//   Swap the color of P and S
		//      <P>             [P]
		//      / \             / \
		//    [X] [S]  ====>  [X] <S>
		//        / \             / \
		//      [C] [D]         [C] [D]
		sibling->color = RED;
		x->father->color = BLACK;
	}
	//Other cases
}

Case 3

兄弟节点 s s s 和侄节点 c c c, d d d 均为黑色，且父节点 p p p 也为黑色。
我们先把兄弟节点 s s s 染红，这样删除目标节点后，父节点 p p p 的所有黑高就相同了。但是这样 p p p 节点的黑高会比兄弟节点少1，所以我们递归维护 p p p。
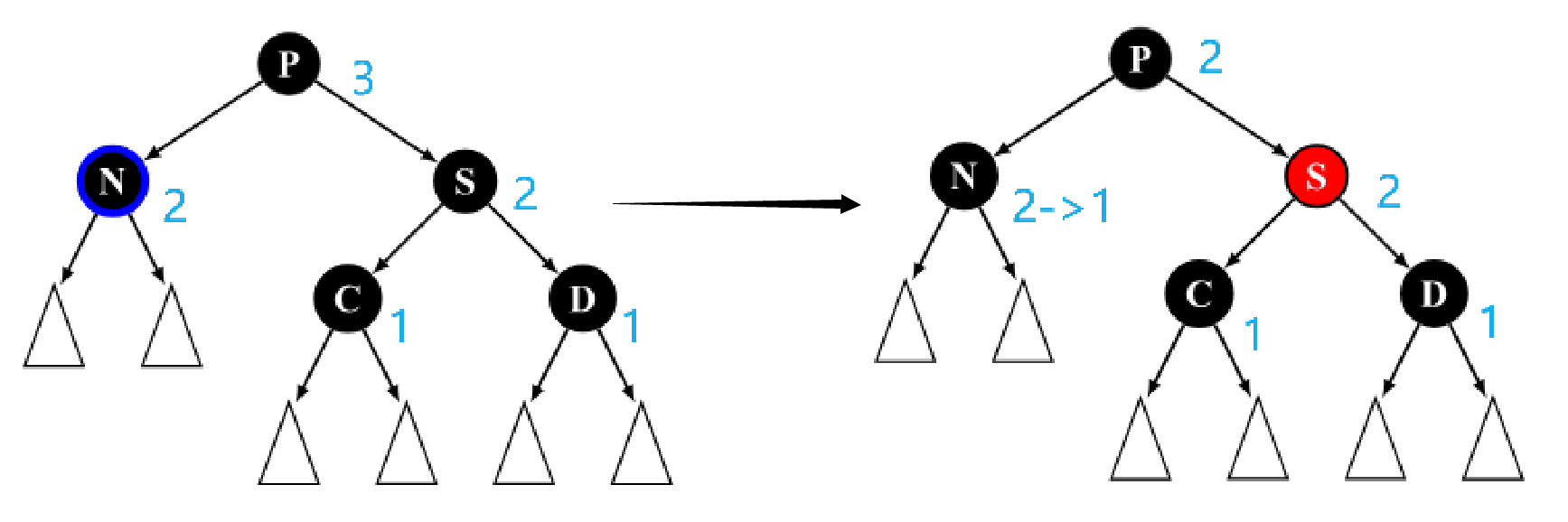
在这里插入图片描述
重新染色后黑高的变化如上图所示。
请添加图片描述

//Assume that both nephews are black
if(x->father->color == BLACK) {
	// Case 3: Sibling, parent and nephews are all black
	//   Step 1. Paint S to RED
	//   Step 2. Recursively maintain P
	//      [P]             [P]
	//      / \             / \
	//    [X] [S]  ====>  [X] <S>
	//        / \             / \
	//      [C] [D]         [C] [D]
	sibling->color = RED;
	SolveDoubleBlack(x->father);
	return;
}

Case 4

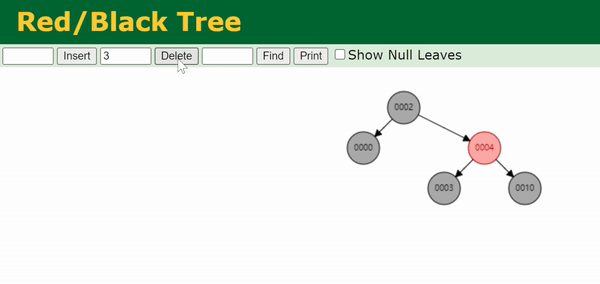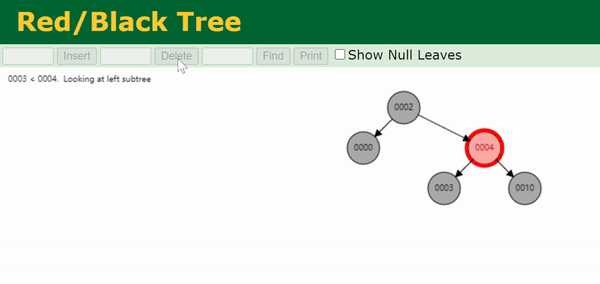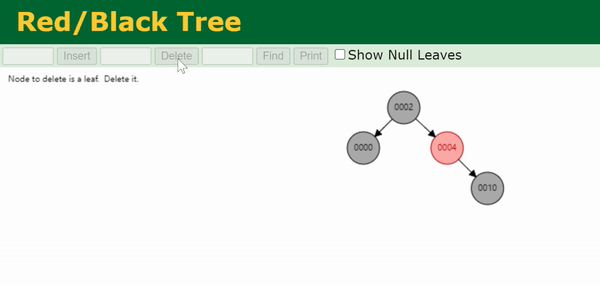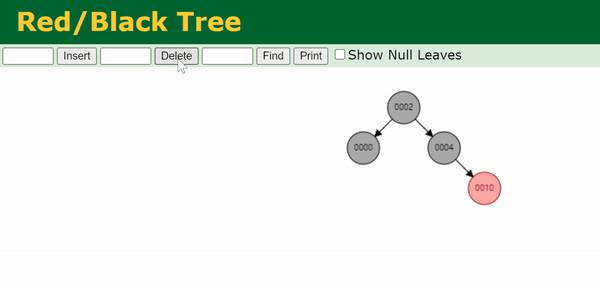
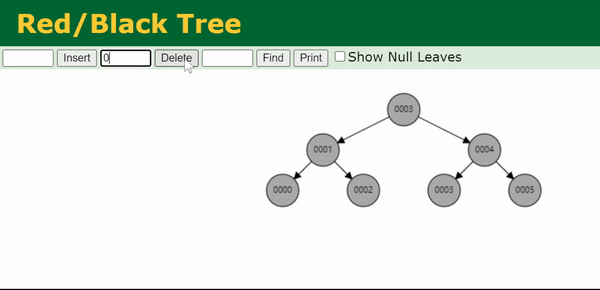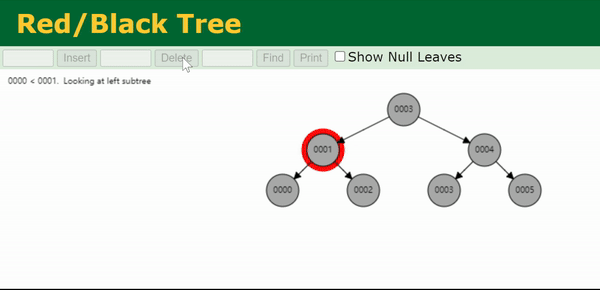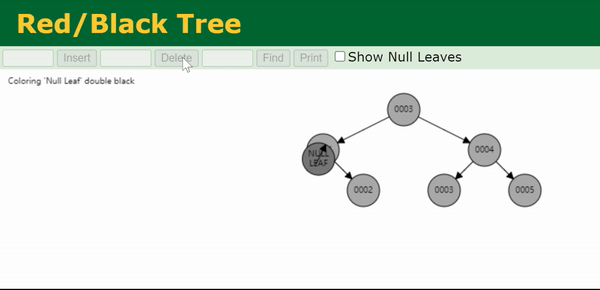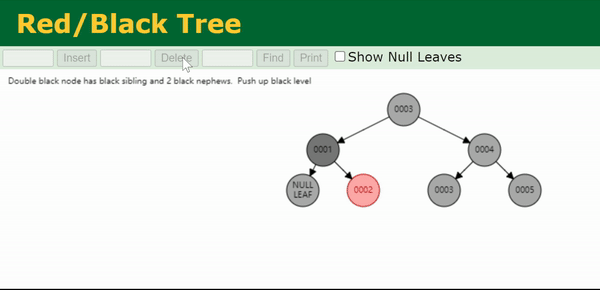
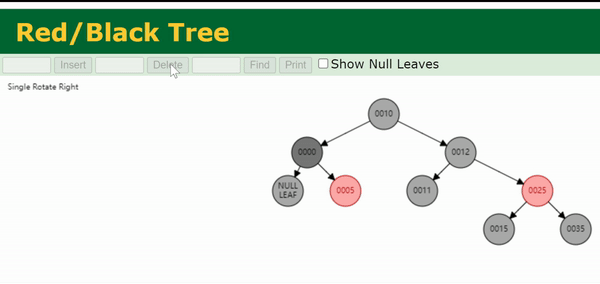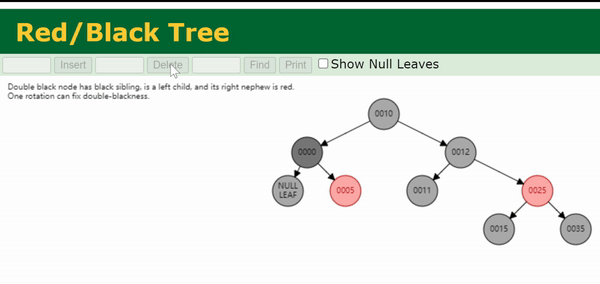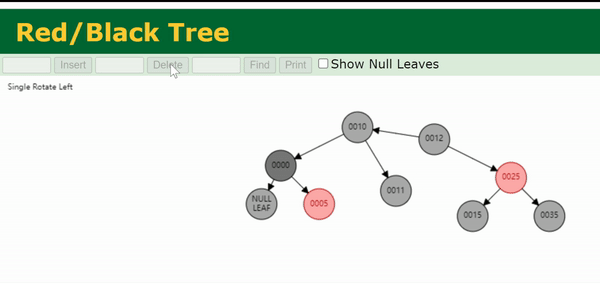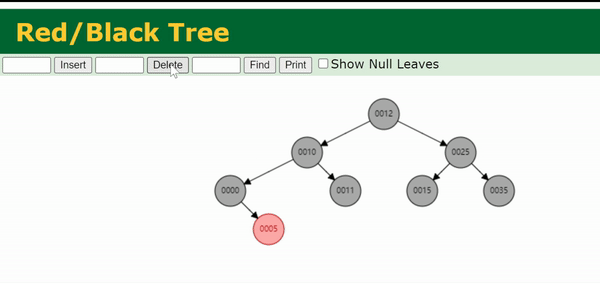
我们把与目标节点同向（即同为左孩子/同为右孩子）的侄节点称为close nephew，用 c c c 表示。反向的侄节点称为distant nephew，用 d d d 表示。在图中可以看出，close nephew就是离目标节点（图中的N）比较近的侄节点，distant nephew就是离得比较远的侄节点。

Case 4为，兄弟节点 s s s 为黑色， c c c 为红， d d d 为黑。父节点 p p p 红黑均可。
这种情况同样无法直接维护，因此将其转变为 Case 5 的状态，利用后续 Case 5 的维护过程进行修正。
Step 1. 向上旋转 c c c
Step 2. 将 c c c 染黑， s s s 染红。
Step 3. 转到 Case 5.
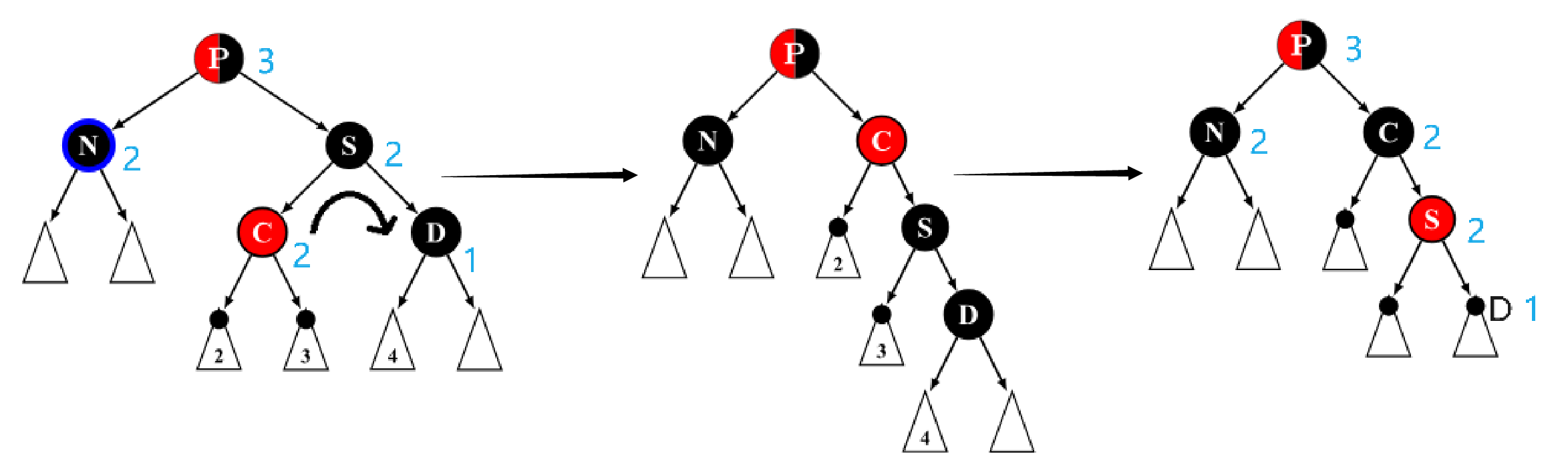
在这里插入图片描述
黑高变化如上图所示。
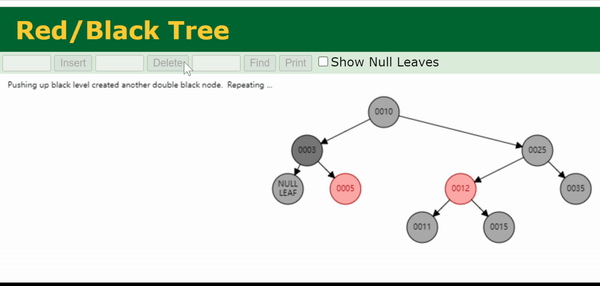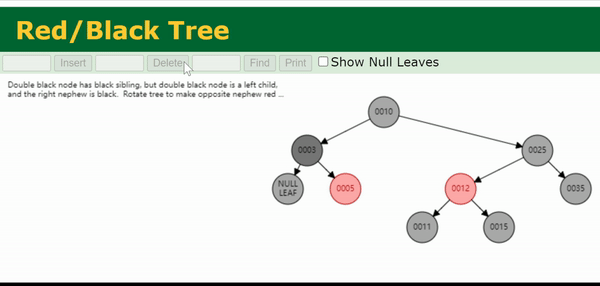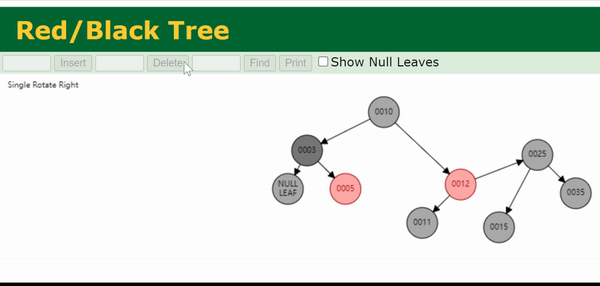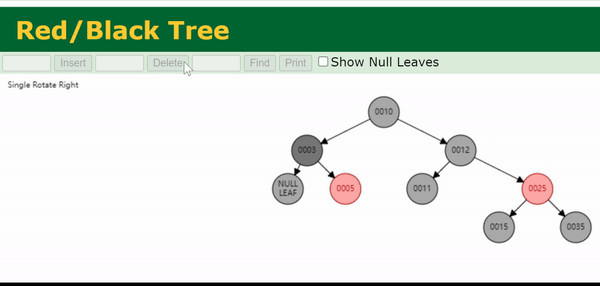
请添加图片描述
注：上面这个gif处理的是0003节点的双黑问题。

bool closeRed = (closeNephew != NULL) && (closeNephew->color == RED);
if(closeRed && distantBlack) {
	// Case 4: Sibling is BLACK, close nephew is RED,
	//         distant nephew is BLACK
	//   Step 1. Rotate close nephew to sibling's position
	//   Step 2. Swap the color of close nephew and sibling
	//   Step 3. Goto case 5
	//                            {P}                {P}
	//      {P}                   / \                / \
	//      / \     rotate(C)   [X] <C>   repaint  [X] [C]
	//    [X] [S]  ==========>        \   ======>        \
	//        / \                     [S]                <S>
	//      <C> [D]                     \                  \
	//                                  [D]                [D]
	//Step 1
	rotate(closeNephew);
	//Step 2
	closeNephew->color = BLACK;
	sibling->color = RED;
	// Update sibling and nephews after rotation
	sibling = x->sibling();
	xdir = x->direction();
	closeNephew = sibling->ch[xdir];
	distantNephew = sibling->ch[xdir ^ 1];
}

Case 5

兄弟节点 s s s 为黑色，distant nephew节点 d d d 为红色，close nephew节点 c c c 为任意颜色，父节点 p p p 为任意颜色。

Step 1. 向上旋转兄弟节点 s s s
Step 2. 把 s s s 染成 p p p 的颜色，把 p p p 染黑（即交换两者颜色）。
Step 3. 将 d d d 染黑。

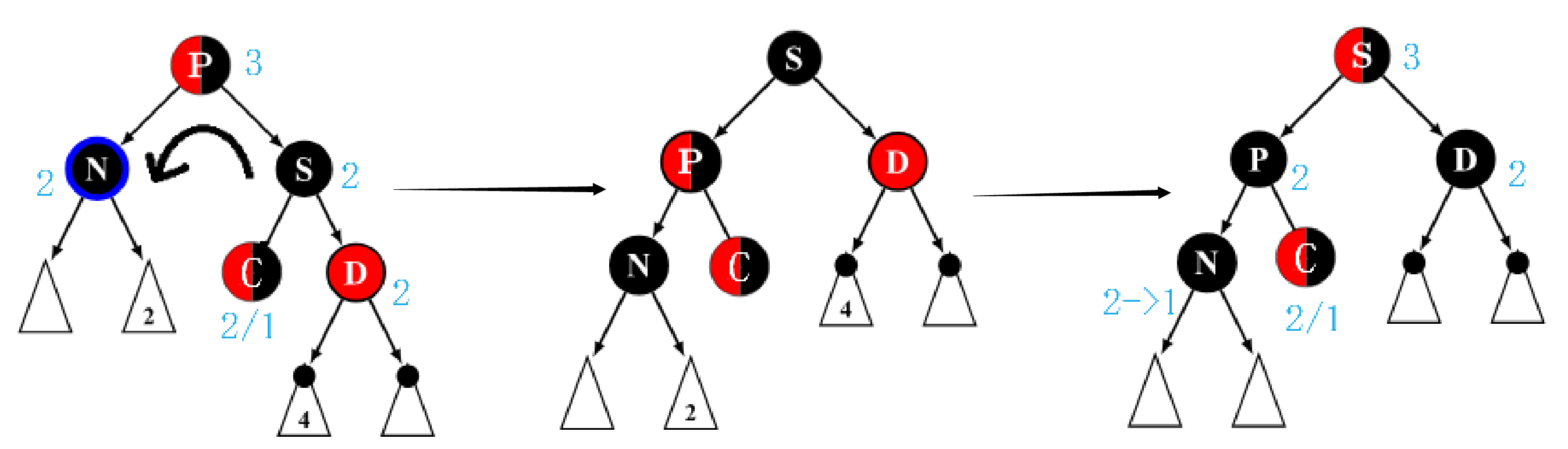
在这里插入图片描述
黑高变化如上图所示。这样操作后删除目标节点，目标节点黑高由2变为1，整棵树满足红黑树性质。
请添加图片描述

	// Case 5: Sibling is BLACK, close nephew is unknown,
	//         distant nephew is RED
	//      {P}                   [S]                 {S}
	//      / \     rotate(S)     / \    repaint     /  \
	//    [X] [S]  ==========>  {P} <D>  =======>  [P]  [D]
	//        / \               / \                / \
	//      {C} <D>           [X] {C}            [X] {C}
	//   Step 1. Rotate sibling to P's position
	//   Step 2. Swap the color of parent and sibling.
	//			 Paint distant nephew to BLACK if it is not null.
	//Step 1
	rotate(sibling);
	//Step 2
	sibling->color = x->father->color;
	x->father->color = BLACK;
	if(distantNephew != NULL) {
		distantNephew->color = BLACK;
	}

其他查询操作

其他查询操作就和二叉查找树完全一致了。下面几个查询操作对应洛谷P3369中的操作3-6.

查询排名

template<typename T>
int RedBlackTree<T>::get_rank(T v, node* x) {
	if(x == NULL)	return 0;
	if(v <= x->val)	return get_rank(v, x->left);
	int lsiz = (x->left != NULL ? x->left->siz : 0);
	return lsiz + 1 + get_rank(v, x->right);
}
template<typename T>
int RedBlackTree<T>::get_rank(T v) {
	return get_rank(v, root);
}

查询第k大

template<typename T>
T RedBlackTree<T>::kth(int k, node* x) {
	if(!(x->left)) {
		if(k == 1)	return x->val;
		return kth(k - 1, x->right);
	}
	if(k <= x->left->siz)	return kth(k, x->left);
	if(k == x->left->siz + 1)	return x->val;
	return kth(k - x->left->siz - 1, x->right);
}
template<typename T>
T RedBlackTree<T>::kth(int k) {
	return kth(k, root);
}

寻找前驱

template<typename T>
T RedBlackTree<T>::get_prev(T v) {
	node *x = root;
	T ans;
	while(x != NULL) {
		if(x->val < v) {
			ans = x->val;
			x = x->right;
		} else {
			x = x->left;
		}
	}
	return ans;
}

寻找后继

template<typename T>
T RedBlackTree<T>::get_succ(T v) {
	node *x = root;
	T ans;
	while(x != NULL) {
		if(x->val > v) {
			ans = x->val;
			x = x->left;
		} else {
			x = x->right;
		}
	}
	return ans;
}

最终代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

template<typename T>
class RedBlackTree {
	private:
		struct node;
		node* root;
		void SolveDoubleRed(node*);
		void SolveDoubleBlack(node*);
		node* Find(T);
		void connect(node*, node*, int);
		void rotate(node*);
		void checkNodeSize(node*);
		
		bool remove(T, node*);
		int get_rank(T, node*);
		T kth(int, node*);
	public:
		RedBlackTree() : root(NULL) {}
		int size();
		void insert(T);
		bool remove(T);
		int get_rank(T);
		T kth(int);
		T get_prev(T);
		T get_succ(T);

		void previs(node*);
		void invis(node*);
		void postvis(node*);
		void print();
		void checkNodeSize();
};

#define RED 1
#define BLACK 0
#define left ch[0]
#define right ch[1]
template<typename T>
struct RedBlackTree<T>::node {
	/*
	 * <X>	X is red.
	 * [X]	X is black.
	 * {X}	X is unknown(red/black).
	 */
	T val;
	bool color;		//1 is red, 0 is black 
	node *father, *ch[2];
	int siz;
	node(T v = T(), bool col = true, node* f = NULL,
	     node* l = NULL, node* r = NULL , int s = 1)
		: val(v), color(col), father(f), siz(s) {
		left = l;
		right = r;
	}
	int direction() {
		if(father == NULL)	return 0;
		return father->right == this;
	}
	node* sibling() {
		if(father == NULL)	return NULL;
		return father->ch[direction() ^ 1];
	}
	bool hasSibling() {
		return sibling() != NULL;
	}
	node* uncle() {
		if(father == NULL)	return NULL;
		return father->sibling();
	}
	bool hasUncle() {
		return uncle() != NULL;
	}
	void pushup() {
		siz = (left?left->siz:0) + (right?right->siz:0) + 1;
	}
	void print() {
		cout << "key = " << val << ", color = " << (color ? "Red" : "Black") << endl;
	}
};

template<typename T>
int RedBlackTree<T>::size() {
	return root->siz;
}

template<typename T>
void RedBlackTree<T>::connect(node *x, node *fa, int k) {
	if(x != NULL)	x->father = fa;
	if(fa != NULL) {
		fa->ch[k] = x;
	} else {
		root = x;
	}
}

template<typename T>
void RedBlackTree<T>::rotate(node *x) {
	//rotate x to its parent's position
	node* y = x->father;
	node* z = y->father;
	int yson = x->direction();
	if(z == NULL) {
		root = x;
		x->father = NULL;
	} else {
		int zson = y->direction();
		connect(x, z, zson);
	}
	connect(x->ch[yson^1], y, yson);
	connect(y, x, yson^1);
	y->pushup();
	x->pushup();
}

template<typename T>
void RedBlackTree<T>::insert(T v) {
	node *x = root, *fa = NULL;
	while(x != NULL) {
		x->siz++;
		fa = x;
		if(v < x->val) {
			x = x->left;
		} else {
			x = x->right;
		}
	}
	x = new node(v, RED, fa);	//create a new node
	if(fa == NULL) {
		root = x;
	} else if(v < fa->val) {
		fa->left = x;
	} else {
		fa->right = x;
	}
	SolveDoubleRed(x);
}
template<typename T>
void RedBlackTree<T>::SolveDoubleRed(node* x) {
	if(x == root || x->father->color == BLACK) {
		return;
	}
	node* p = x->father;
	if(p == root) {
		// Case 3: Parent is root and is RED
		//   Paint parent to BLACK.
		//    <P>         [P]
		//     |   ====>   |
		//    <X>         <X>
		p->color = BLACK;
		return;
	}
	if(x->hasUncle() && x->uncle()->color == RED) {
		// Case 4: Both parent and uncle are RED
		//   Paint parent and uncle to BLACK;
		//   Paint grandparent to RED;
		//   Maintain grandparent recursively.
		//        [G]             <G>
		//        / \             / \
		//      <P> <U>  ====>  [P] [U]
		//      /               /
		//    <X>             <X>
		p->color = BLACK;			//parent -> black
		x->uncle()->color = BLACK;	//uncle  -> black
		p->father->color = RED;		//grandparent -> red
		SolveDoubleRed(p->father);
		return;
	}
	// Case 5 & 6: parent is RED, uncle is BLACK(or NULL)
	if(x->direction() != p->direction()) {
		// Case 5: Current node is the opposite direction as parent
		//   Step 1. Rotate x to parent's position.
		//   Step 2. Goto Case 6.
		//      [G]                 [G]
		//      / \    rotate(X)    / \
		//    <P> [U]  ========>  <X> [U]
		//      \                 /
		//      <X>             <P>
		rotate(x);
		x = p;			//Now P is the child of double red.
		p = x->father;	//reset p to x's father
	}
	// Case 6: Current node is the same direction as parent
	//   Step 1. Rotate parent to grandparent's position
	//   Step 2. Paint parent (before rotate) to BLACK;
	//           Paint grandparent (before rotate) to RED.
	//        [G]                 <P>               [P]
	//        / \    rotate(P)    / \    repaint    / \
	//      <P> [U]  ========>  <X> [G]  ======>  <X> <G>
	//      /                         \                 \
	//    <X>                         [U]               [U]
	rotate(p);				//rotate x's parent
	p->color = BLACK;
	x->sibling()->color = RED;	//repaint
}

#define col(a) (a == RED ? "Red" : "Black")

template<typename T>
void RedBlackTree<T>::previs(node* x) {
	if(x == NULL)	return;
	printf("%d %s %d\n", x->val, col(x->color), x->siz);
	previs(x->left);
	previs(x->right);
}
template<typename T>
void RedBlackTree<T>::invis(node* x) {
	if(x == NULL)	return;
	invis(x->left);
	printf("%d %s %d\n", x->val, col(x->color), x->siz);
	invis(x->right);
}
template<typename T>
void RedBlackTree<T>::postvis(node* x) {
	if(x == NULL)	return;
	postvis(x->left);
	postvis(x->right);
	printf("%d %s %d\n", x->val, col(x->color), x->siz);
}
template<typename T>
void RedBlackTree<T>::print() {
	printf("------pre-vis------\n");
	previs(root);
	printf("------in-vis------\n");
	invis(root);
	printf("------post-vis------\n");
	postvis(root);
}

template<typename T>
void RedBlackTree<T>::checkNodeSize(node* x) {
	int before = x->siz;
	if(x->left)	checkNodeSize(x->left);
	if(x->right)	checkNodeSize(x->right);
	x->pushup();
	if(x->siz != before) {
		printf("node of key %d : size changed from %d to %d\n", x->val, before, x->siz);
	}
}

template<typename T>
void RedBlackTree<T>::checkNodeSize() {
	checkNodeSize(root);
}

template<typename T>
bool RedBlackTree<T>::remove(T v) {
	return remove(v, root);
}

template<typename T>
bool RedBlackTree<T>::remove(T v, node* x) {
	if(x == NULL)	return false;
	if(v != x->val) {
		int branch = (v > x->val);	//v > x->val : branch = 1, goto right child
		if(x->ch[branch] != NULL) {
			//the structure of the subtree may change
			//node x may have new children after remove
			//so first update the size of subtree
			//if fail to remove then rollback size changes
			x->siz--;
			bool result = remove(v, x->ch[branch]);
			if(result == false) {
				x->siz++;
			}
			return result;
		}
		return false;
	}
	if(x == root && x->siz == 1) {
		root = NULL;
		return true;
	}
	if(x->left != NULL && x->right != NULL) {
		// Case 1: If the node is strictly internal
		//   Step 1. Find the successor S with the smallest key
		//           and its parent P on the right subtree.
		//   Step 2. Swap the data (key and value) of S and X,
		//           S is the node that will be deleted in place of X.
		//   Step 3. X = S, goto Case 2, 3
		//     |                    |
		//     X                    S
		//    / \                  / \
		//   L  ..   swap(X, S)   L  ..
		//       |   =========>       |
		//       P                    P
		//      / \                  / \
		//     S  ..                X  ..
		x->siz--;
		//Step 1
		node* rt = x->right;
		rt->siz--;
		while(rt->left) {
			rt = rt->left;
			rt->siz--;
		}
		//Step 2, 3
		node* succ = rt;
		swap(x->val, succ->val);
		x = succ;
	}
	if(x->left == NULL && x->right == NULL) {
		// Case 2: Current node is a leaf
		//   Step 1. Put X to a position where its black height
		//           is greater than its sibling by 1.(if X is black)
		//   Step 2. remove X

		// The maintain operation won't change the node itself,
		//  so we can perform maintain operation before unlink the node.
		x->siz = 0;
		if(x->color == BLACK) {
			SolveDoubleBlack(x);	//Step 1
		}
		x->father->ch[x->direction()] = NULL;
		x->father->pushup();
		return true;
	}
	// Case 3: Current node has a single left or right child
	//   Step 1. Paint its child to black(the child must be red).
	//   Step 2. Remove X
	node* replacement = (x->left != NULL ? x->left : x->right);
	if(x->color == BLACK) {
		replacement->color = BLACK;
	}
	if(x == root) {
		root = replacement;
		replacement->father = NULL;
	} else {
		node* parent = x->father;
		parent->ch[x->direction()] = replacement;
		replacement->father = parent;
		parent->pushup();
	}
	return true;
}

template<typename T>
void RedBlackTree<T>::SolveDoubleBlack(node* x) {
	if(x == root)	return;
	node* sibling = x->sibling();
	if(sibling->color == RED) {
		// Case 1: Sibling is RED, parent and nephews must be BLACK
		//   Step 1. Rotate X's sibling to P's position
		//   Step 2. Paint S to BLACK, P to RED
		//   Step 3. Goto Case 2, 3, 4, 5
		//      [P]                   <S>               [S]
		//      / \     rotate(S)     / \    repaint    / \
		//    [X] <S>  ==========>  [P] [D]  ======>  <P> [D]
		//        / \               / \               / \
		//      [C] [D]           [X] [C]           [X] [C]
		node* parent = x->father;
		//Step 1
		rotate(sibling);
		//Step 2
		sibling->color = BLACK;
		parent->color = RED;
		sibling = x->sibling();		//update sibling after rotation
	}
	//close nephew: sibling's child with the same direction as x
	int xdir = x->direction();		//the direction of x
	node* closeNephew = sibling->ch[xdir];
	node* distantNephew = sibling->ch[xdir ^ 1];
	//NIL nodes are always black
	bool closeBlack = (closeNephew == NULL) || (closeNephew->color == BLACK);
	bool distantBlack = (distantNephew == NULL) || (distantNephew->color == BLACK);
	if(closeBlack && distantBlack) {
		if(x->father->color == RED) {
			// Case 2: Sibling and nephews are BLACK, parent is RED
			//   Swap the color of P and S
			//      <P>             [P]
			//      / \             / \
			//    [X] [S]  ====>  [X] <S>
			//        / \             / \
			//      [C] [D]         [C] [D]
			sibling->color = RED;
			x->father->color = BLACK;
		} else {
			// Case 3: Sibling, parent and nephews are all black
			//   Step 1. Paint S to RED
			//   Step 2. Recursively maintain P
			//      [P]             [P]
			//      / \             / \
			//    [X] [S]  ====>  [X] <S>
			//        / \             / \
			//      [C] [D]         [C] [D]
			sibling->color = RED;
			SolveDoubleBlack(x->father);
		}
	} else {
		bool closeRed = (closeNephew != NULL) && (closeNephew->color == RED);
		if(closeRed && distantBlack) {
			// Case 4: Sibling is BLACK, close nephew is RED,
			//         distant nephew is BLACK
			//   Step 1. Rotate close nephew to sibling's position
			//   Step 2. Swap the color of close nephew and sibling
			//   Step 3. Goto case 5
			//                            {P}                {P}
			//      {P}                   / \                / \
			//      / \     rotate(C)   [X] <C>   repaint  [X] [C]
			//    [X] [S]  ==========>        \   ======>        \
			//        / \                     [S]                <S>
			//      <C> [D]                     \                  \
			//                                  [D]                [D]
			//Step 1
			rotate(closeNephew);
			//Step 2
			closeNephew->color = BLACK;
			sibling->color = RED;
			// Update sibling and nephews after rotation
			sibling = x->sibling();
			xdir = x->direction();
			closeNephew = sibling->ch[xdir];
			distantNephew = sibling->ch[xdir ^ 1];
		}
		// Case 5: Sibling is BLACK, close nephew is unknown,
		//         distant nephew is RED
		//      {P}                   [S]                 {S}
		//      / \     rotate(S)     / \    repaint     /  \
		//    [X] [S]  ==========>  {P} <D>  =======>  [P]  [D]
		//        / \               / \                / \
		//      {C} <D>           [X] {C}            [X] {C}
		//   Step 1. Rotate sibling to P's position
		//   Step 2. Swap the color of parent and sibling.
		//			 Paint distant nephew to BLACK if it is not null.
		//Step 1
		rotate(sibling);
		//Step 2
		sibling->color = x->father->color;
		x->father->color = BLACK;
		if(distantNephew != NULL) {
			distantNephew->color = BLACK;
		}
	}
}

template<typename T>
T RedBlackTree<T>::kth(int k, node* x) {
	if(!(x->left)) {
		if(k == 1)	return x->val;
		return kth(k - 1, x->right);
	}
	if(k <= x->left->siz)	return kth(k, x->left);
	if(k == x->left->siz + 1)	return x->val;
	return kth(k - x->left->siz - 1, x->right);
}
template<typename T>
T RedBlackTree<T>::kth(int k) {
	return kth(k, root);
}

template<typename T>
T RedBlackTree<T>::get_prev(T v) {
	node *x = root;
	T ans;
	while(x != NULL) {
		if(x->val < v) {
			ans = x->val;
			x = x->right;
		} else {
			x = x->left;
		}
	}
	return ans;
}
template<typename T>
T RedBlackTree<T>::get_succ(T v) {
	node *x = root;
	T ans;
	while(x != NULL) {
		if(x->val > v) {
			ans = x->val;
			x = x->left;
		} else {
			x = x->right;
		}
	}
	return ans;
}

template<typename T>
int RedBlackTree<T>::get_rank(T v, node* x) {
	if(x == NULL)	return 0;
	if(v <= x->val)	return get_rank(v, x->left);
	int lsiz = (x->left != NULL ? x->left->siz : 0);
	return lsiz + 1 + get_rank(v, x->right);
}
template<typename T>
int RedBlackTree<T>::get_rank(T v) {
	return get_rank(v, root);
}
RedBlackTree<int> Tree;
int main() {
	int n;
	cin >> n;
	while(n--) {
		int op, x;
		cin >> op >> x;
		if(op == 1) {
			Tree.insert(x);
		} else if(op == 2) {
			Tree.remove(x);
		} else if(op == 3) {
			cout << Tree.get_rank(x) + 1 << endl;
		} else if(op == 4) {
			cout << Tree.kth(x) << endl;
		} else if(op == 5) {
			cout << Tree.get_prev(x) << endl;
		} else {
			cout << Tree.get_succ(x) << endl;
		}
//		Tree.checkNodeSize();
	}
	return 0;
}
ILoveFujibayashiRyou
关注
  • 33
    点赞
  • 踩
  • 18
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
通过Java实现红黑树及其可视化
12-09
通过Java实现红黑树及其可视化 对于节点的定义，包含节点的数值、节点的颜色、节点的父节点、节点的左右叶子结点 通过Java实现红黑树，包括红黑树的插入操作、删除操作、维护红黑树性质的操作以及常用的方法函数...
机器学习-决策树实现可视化
01-20
机器学习- 决策树实现可视化 要安装库sklearn，pandas，graphviz在cmd中安装 pip install sklearn pip install pandas pip install graphviz 下载graphviz，装环境变量 下载网址：在下载的时候有点慢...
KD树详解
weixin_39568744的博客
05-17 8516
转载自：https://blog.csdn.net/xbmatrix/article/details/63683614 2.1、什么是KD树 Kd-树是K-dimension tree的缩写，是对数据点在k维空间（如二维(x，y)，三维(x，y，z)，k维(x1，y，z..)）中划分的一种数据结构，主要应用于多维空间关键数据的搜索（如：范围搜索和最近邻搜索）。本质上说，Kd-树就是一种...
KD树详解及KD树最近邻算法
生活不止眼前的枸杞， 还有蜂蜜和咖啡！
06-08 5318
&amp;nbsp; &amp;nbsp; 一般说来，索引结构中相似性查询有两种基本的方式： 一种是范围查询，范围查询时给定查询点和查询距离阈值，从数据集中查找所有与查询点距离小于阈值的数据另一种是K近邻查询，就是给定查询点及正整数K，从数据集中找到距离查询点最近的K个数据，当K=1时，它就是最近邻查询。&amp;nbsp; &amp;nbsp; 同样，针对特征点匹配也有两种方法： 最容易的办法就是线性扫描，也就是我们常...
机器学习算法（二十五）：KD树详解及KD树最近邻算法
热门推荐
weixin_39910711的博客
03-06 1万+
目录 1 KD树 1.1什么是KD树 1.2KD树的构建 1.3 KD树的插入 1.4KD树的删除 1.5KD树的最近邻搜索算法 1.5.1举例：查询点（2.1,3.1） 1.5.2 举例：查询点（2，4.5） 2 kd树近邻搜索算法的改进：BBF算法 3 球树、M树、VP树、MVP树 3.1球树 3.2VP树与MVP树简介 特征点匹配和数据库查、图像检索本质上是同一个问题，都可以归结为一个通过距离函数在高维矢量之间进行相似性检索的问题，如何快速而准确...
KNN（三）--KD树详解及KD树最近邻算法
__kingzone__的专栏
05-22 5115
之前blog内曾经介绍过SIFT特征匹配算法，特征点匹配和数据库查、图像检索本质上是同一个问题，都可以归结为一个通过距离函数在高维矢量之间进行相似性检索的问题，如何快速而准确地找到查询点的近邻，不少人提出了很多高维空间索引结构和近似查询的算法。    一般说来，索引结构中相似性查询有两种基本的方式：一种是范围查询，范围查询时给定查询点和查询距离阈值，从数据集中查找所有与查询点距离小于阈值的数据另一...
决策树可视化.rar决策树可视化.rar
03-17
决策树可视化.rar
基于QT实现B树可视化程序设计.zip
06-24
本例在实现基础功能的基础上，用QT做了B树的可视化： 1."/src/BTree"文件中的是原始代码，可以通过控制台对B树操作，并在控制台中可视化； 2."/src/BTreeDisplay"文件中是QT可视化工程代码。用对话框和QT绘制实现B树...
Python决策树可视化代码.zip
02-06
id3算法创建决策树，用matplotlib库实现决策树可视化（机器学习入门）
栈和队列--数据结构
m0_72565784的博客
04-25 613
一种特殊的线性表，其只。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵循“后进先出”（LIFO）的原则。
【数据结构】图的应用（最小生成树、拓扑排序、最短路径等）
2201_75475240的博客
04-27 1263
本文章介绍数据结构中的图的应用，包括最小生成树的Prim算法和Kruskal算法，拓扑排序和最短路径，且还包含408习题（附有解析）。此外，含有关于Prim算法，Kruskal算法和Dijkstra算法全部具体实现代码。
【数据结构】二叉树（带图详解）
Z1tai的博客
04-27 1501
链表和数组都是线性结构，而树是非线性的结构。树是依靠分支关系定义出的一种层次结构。社会亲缘关系和组织结构图都可以用树来形象地表示。
数据结构系列-二叉树之前序遍历
in_seattle的博客
04-26 466
这篇文章，我们主要的内容是对二叉树当中的前历的算法进行讲解，二叉树中的算法所要求实现的是 从根到左子树再到右子树的遍历顺序，可能这样不太好理解，我们拿一张图片进行解释，我们先来分析一下这个的实现逻辑是什么，按照根节点，左子树，右子树的顺序，我们先来判断一下这个应该实现的结果是什么。在这里，我们将空也表现了出来，那下面，我们就讲解一下怎么用代码实现这个过程。假设在这个二叉树当中，我们要实现二叉树遍历当中的前历，我们应该怎么做呢。这些代码我们在前面就详细的进行了展开，在这里我们就不进行详细的讲解。
【数据结构】第二章 线性数据结构.线性表.顺序表
KX_52517的博客
04-26 1334
线性数据结构章节
《数据结构》（学习笔记）（王道）
qiqi_liuliu的博客
04-23 620
Personal study notes, please point out any errors, thank you!
数据结构––队列
最新发布
2301_80190473的博客
04-27 240
【代码】数据结构––队列。
数据结构练习：链表扩容
2301_80369371的博客
04-25 289
一：创建一个新链表，遍历原链表的同时，将原链表的值复制给新链表。二：将新链表插入到原链表中（大致如下）3.*&是c++的写法，等同于c中的*2.记得malloc后要free。1.头结点是不存有数据的。
数据结构(八)——排序
señoritaw的博客
04-25 1054
排序(Sort)，就是重新排列表中的元素，使表少的元素满足按关键字有序的过程。输入∶n个记录R1,R2...., Rn，对应的关键字为k1, k2,... , kn输出:输入序列的一个重排R1',R2'....,Rn'，使得有k1'≤k2'≤...≤kn'(也可递减)算法的稳定性。若待排序表中有两个元素R,和R，其对应的关键字相同即key = keyj，且在排序前R;在R,的前面，若使用某一排序算法排序后，R仍然在R的前面，则称这个排序算法是稳定的，否则称排序算法是不稳定的。
graphviz决策树可视化代码详解
11-06
graphviz是一个开源的可视化工具，可以用来绘制各种图形，包括决策树。下面是对上述代码的详细解释： 1. 首先导入需要的库：from sklearn.tree import export_graphviz, import graphviz, os 2. 接着，我们需要将Graphviz的bin目录添加到环境变量中，这样才能在Python中调用Graphviz。这里使用了os.environ['PATH'] = os.pathsep + r'C:\Program Files (x86)\Graphviz2.38\bin'来手动进行环境变量配置。 3. 然后，我们使用export_graphviz函数将决策树模型导出为Graphviz格式的数据。其中，model是我们训练好的决策树模型，class_names是我们分类的类别名称。 4. 接着，我们使用graphviz.Source函数将Graphviz格式的数据转换为可视化的图形。 5. 最后，我们使用graph.render函数将可视化的图形保存为一个PDF文件，文件名为'决策树可视化'。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值