机器学习论文及代码浅读：LassoNet

thorn_r

已于 2024-01-01 14:07:28 修改

阅读量1.5k

点赞数 20

文章标签：机器学习 python

于 2023-12-28 17:01:14 首次发布

本文链接：https://blog.csdn.net/thorn_r/article/details/135241976

版权

论文地址：https://arxiv.org/abs/1907.12207

代码地址：GitHub - lasso-net/lassonet: Feature selection in neural networks

在机器学习的过程中，特征筛选能够过滤冗余信息，增加模型可解释性，提高计算速度减少内存，甚至提升模型的泛化能力。然而，尽管在线性回归中有着广泛的研究，如Lasso，Ridge，Elastic-Net；神经网络中的特征筛选依然是一项“公开的挑战”。

零、相关工作

一般的特征选择方法可以分为三类：过滤器，包装器和嵌入式。

使用过滤器筛选特征通常是独立于学习器（模型）方法的。如Fisher score，用各个数据点的距离来做特征筛选。这也限制了此类的特征筛选方法无法检测到交互特征。

而使用包装法来筛选特征主要依赖于学习器的算法本身在学习的过程中做特征筛选。

嵌入式则是融合了过滤器与包装器两个方法：在使用正式的学习器进行学习前，先使用1个模型专门用来做特征筛选或预处理。

论文中的LassoNet实际上就是提出的一种“包装法”特征筛选。

一、模型架构

LassoNet的核心思想，是使用一个“Skip层”（绿色）的结构来控制要进入后面隐层的特征数量，从而实现特征的稀疏化。它的目标函数是：

$minimize_{\theta,W} L(\theta,W) + \lambda ||\theta||_1$

且对于神经网络中的每一个隐藏层，都有如下限制：

$|W_{jk}^{(1)}|\leq M\cdot |\theta_j|,k=1,...,d$

其中， $\theta$ 表示skip层的权重，其范数也是正则项，同时也是损失函数中的L1正则项； $\lambda$ 表示L1正则项的系数；而 $W_{jk}^{(1)}$ 代表第一层隐藏层中第j个特征的权重，当 $\theta_j=0$ 时，j特征不会参与到后面隐藏层的计算；M代表层次系数，控制线性和非线性强度的一个系数。

其中， $\lambda$ 和 $M$ 这2个参数可以被视作超参数。对于M在没有专家知识的情况下，我们可以使用朴素搜索等方式根据验证集验证这个超参。而对于 $\lambda$ 而言，尽管在论文中说是LassoNet的两大“超参数”之一，但实际上在LassoNet的训练过程中，是会更新这一值的，详细的过程笔者会在第四节说明。

二、算法大致流程

下图是LassoNet的算法流程：

从第6到第8行就是普通的隐藏层反向传播的过程，在此过程中已经加上了，之后还使用了一个“Hier-Prox”算法；这个算法的主要作用应该就是针对第一层隐藏层和skip层根据 $\lambda$ 和M做二次更新；其具体原理以及实现笔者具体写在第三节。

具体在代码中如下实现：

n_train = len(X_train)
if batch_size is None:
	batch_size = n_train
	randperm = torch.arange
else:
	randperm = torch.randperm
batch_size = min(batch_size, n_train)

for epoch in range(epochs):
	indices = randperm(n_train)
	model.train()
	loss = 0
	for i in range(n_train // batch_size):
		# don't take batches that are not full
		batch = indices[i * batch_size : (i + 1) * batch_size]

		#closure的作用是在optimizer.step梯度下降时对loss做的函数；
		#在做优化前就会运行；此处将loss的backward函数放在这个closure函数里面
		#这样就相当于在计算梯度之前，先把loss加上了惩罚项
		def closure():
			nonlocal loss
			optimizer.zero_grad()
			ans = (
				self.criterion(model(X_train[batch]), y_train[batch])
				+ self.gamma * model.l2_regularization()
				+ self.gamma_skip * model.l2_regularization_skip()
			)
			if ans + 1 == ans:
				print(f"Loss is {ans}", file=sys.stderr)
				print(f"Did you normalize input?", file=sys.stderr)
				print(
					f"Loss: {self.criterion(model(X_train[batch]), y_train[batch])}"
				)
				print(f"l2_regularization: {model.l2_regularization()}")
				print(
					f"l2_regularization_skip: {model.l2_regularization_skip()}"
				)
				assert False
			ans.backward() #相当于第7行Compute gradient of the loss
			loss += ans.item() * len(batch) / n_train
			return ans

		optimizer.step(closure) #相当于第8行Update theta and W
		model.prox(lambda_=lambda_ * optimizer.param_groups[0]["lr"], M=self.M) #Hier-Prox算法

这里定义的closure函数会在optimizer.step()的过程中首先运行，相当于将loss.backward()过程和optimizer.step()过程做了合并。这里的closure函数最大的作用，其实就是替代了原本的loss.backward()；重新在原本的损失函数（self.criterion）上增加了模型的正则项（l2_regularization；l1部分只会在验证时使用）。之后，运行Hier-Prox算法再次根据超参 $\lambda$ 和M再次更新第一层隐藏层与skip层。

唯一和伪代码不同之处就在于，伪代码中的K循环直至所有的特征全部都筛选出去，而此处是将它改变为了将所有计算出可能的 $\lambda$ 值遍历一遍：

for current_lambda in itertools.chain([lambda_start], lambda_seq):
	if self.model.selected_count() == 0:
		break
	last = self._train(
		X_train,
		y_train,
		X_val,
		y_val,
		batch_size=self.batch_size,
		lambda_=current_lambda,
		epochs=self.n_iters_path,
		optimizer=optimizer,
		patience=self.patience_path,
		return_state_dict=return_state_dicts,
	) #Compute gradient of the loss

三、Hier-Prox算法

这是一个“近端梯度优化问题”。原本模型损失函数的正则项部分 $\lambda ||\theta||_1$ 导致了这个损失函数本身是不可微的，故而需要使用一个特殊的优化方法（近端梯度优化；更准确地说，这里被称为迭代收缩阈值suanfa(ISTA)）来寻求全局最优。

论文中给出了这个目标优化公式，是Hier-Prox算法的优化对象，但是这个公式中的u,v和b的含义都没有给出，因为论文中只是给出了Hier-Prox算法优化对对象的“通用形式”（finds the global minimum of an optimization problem of the form）。我的理解是：u代表第一个隐藏层的权重矩阵，v代表skip层的权重；b和W分别代表能够使得网络全局最优的skip层的权重与第一个隐藏层的权重。这个公式的限制条件是一个不等式。这样的不等式约束求最优解，需要用到KKT条件，笔者的最优化领域知识与代数能力有限，此处只给出论文中的结论，具体证明可参考论文的附录B。

2024-01-01更新：附上了Hier-Prox算法的证明，但是只有W部分的证明看懂了，b部分的证明尚在整理。

这个伪代码中的各个公式就是KKT条件优化之后得到的结果，但是如果看代码的话，可能会觉得“货不对板”，因为代码中的prox函数实际上是一个更为“一般化”的Hier-Prox算法，其中的a_s，u，v等变量实际上是应该看附录B中的证明过程得来的。

def prox(v, u, *, lambda_, lambda_bar, M):
    """
    v has shape (m,) or (m, batches)
    u has shape (k,) or (k, batches)

    
    最初此处v传入beta,u传入theta
    beta为skip层，theta为网络第一层； 此处与论文里的希腊字母theta应该是反的
    不断迭代更新beta和theta，直至beta收敛到1e-5以下

    此处就是论文中的Algorithm 2:Hier-Prox

    supports GPU tensors
    """
    onedim = len(v.shape) == 1
    if onedim:
        v = v.unsqueeze(-1)
        u = u.unsqueeze(-1)

    u_abs_sorted = torch.sort(u.abs(), dim=0, descending=True).values

    k, batch = u.shape

    s = torch.arange(k + 1.0).view(-1, 1).to(v) #公式中的m
    zeros = torch.zeros(1, batch).to(u)#这个zeros我推测是常数项？

    a_s = lambda_ - M * torch.cat(
        [zeros, torch.cumsum(u_abs_sorted - lambda_bar, dim=0)]
    ) #后半段是s_lambda函数中的那个M*累加的公式

    norm_v = torch.norm(v, p=2, dim=0)

    x = F.relu(1 - a_s / norm_v) / (1 + s * M ** 2) 
    #前面那个"1-"和relu函数应该是论文里面的函数S_lambda=sign(x)*max{|x|-lambda,0}
    # 此处的带有"1-"的公式就是证明里面的b_s

    w = M * x * norm_v #wm；但是缺示性函数
    intervals = soft_threshold(lambda_bar, u_abs_sorted)
    lower = torch.cat([intervals, zeros]) #示性函数最后单独写在这里

    idx = torch.sum(lower > w, dim=0).unsqueeze(0)

    x_star = torch.gather(x, 0, idx).view(1, batch)
    w_star = torch.gather(w, 0, idx).view(1, batch) #w_star应该是论文中的w_m^~


    beta_star = x_star * v #x_star相当于w_star/(M*norm_v)；之后又乘上原始的v，此处没有看懂
    theta_star = sign_binary(u) * torch.min(soft_threshold(lambda_bar, u.abs()), w_star) #没看懂为什么这里有个soft_threshold；而且lambda_bar=0……

    if onedim:
        beta_star.squeeze_(-1)
        theta_star.squeeze_(-1)

    return beta_star, theta_star

文中介绍说Hier-Prox算法的时间复杂度为O(p·log p)，p=dK+d，d是特征数量，K是第一层隐藏层的单元数；认为这个算法在相较于普通的BP算法而言降低了许多开销。

四、Warm Start计算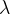 $\lambda$

论文中只是简短地提到了在优化lambda时，使用上一个用完的lambda作为下一个warm start的启动项，并且从密集到稀疏的过程效果优化效果更好，这边还是看一下代码吧。

# build lambda_seq
if lambda_seq is not None:
	pass
elif self.lambda_seq is not None:
	lambda_seq = self.lambda_seq
else:

	def _lambda_seq(start):
		while start <= lambda_max:
			yield start
			start *= self.path_multiplier #path_multiplier:1+epsilon

	if self.lambda_start == "auto":
		# divide by 10 for initial training
		self.lambda_start_ = (
			self.model.lambda_start(M=self.M) #计算lambda_start的值
			/ optimizer.param_groups[0]["lr"]
			/ 10
		)
		lambda_seq = _lambda_seq(self.lambda_start_)
	else:
		lambda_seq = _lambda_seq(self.lambda_start)

# extract first value of lambda_seq
lambda_seq = iter(lambda_seq)
lambda_start = next(lambda_seq)

is_dense = True


for current_lambda in itertools.chain([lambda_start], lambda_seq):
    # ** 之后开始Algorithm 1 **
	...

可以看出，在实际训练神经网络时这个lambda是被定死为一个值的；但是在训练之前，就已经会根据初值计算出一系列的lambda值然后在这一些列的lambda中做循环了。

所有的lambda值其实就是根据之前的lambda乘以一个定值（默认是1.02）以此加大惩罚项的系数，实现“从密集到稀疏”的过程。

而lambda初值，出去固定给一个值以外，还有个“auto”的计算初值的方法：

def lambda_start(
	self,
	M=1,
	lambda_bar=0,
	factor=2,
):
	"""Estimate when the model will start to sparsify."""

	def is_sparse(lambda_):
		with torch.no_grad():
			beta = self.skip.weight.data
			theta = self.layers[0].weight.data

			for _ in range(10000):
				new_beta, theta = prox(
					beta,
					theta,
					lambda_=lambda_,
					lambda_bar=lambda_bar,
					M=M,
				)
				if torch.abs(beta - new_beta).max() < 1e-5:
					break
				beta = new_beta
			return (torch.norm(beta, p=2, dim=0) == 0).sum()

	start = 1e-6
	while not is_sparse(factor * start):
		start *= factor
	return start

我对此处的个人理解是：此处的beta和theta是尚未训练的权重；而使用is_parse函数就是在模拟做Hier-Prox算法；倘若在Hier-Prox算法完成后，没有特征被筛选出去（即特征依然密集），那么就可以将这个lambda作为最初始的lambda。

五、总结

论文提出了一个在神经网络中能够做特征提取的结构：LassoNet，其核心思想，是使用一个“Skip层”的结构来控制要进入后面隐层的特征数量，从而实现特征的稀疏化。尽管原理看上去很简单，但是针对其进行反向传播的优化算法（Warm Start和Hier-Prox算法），实际上有着相当的数学最优化原理。这篇论文实际上结合了原本线性模型种的L1正则化与ResNet的思路，可以说有着借鉴价值。

附：Hier-Prox算法的证明

Hier-Prox算法是希望能够解决上图的凸优化问题；LassoNet中的优化问题是 $\overline{\lambda}=0$ 的一个特殊形式。（因为Lasso部分是加在skip层而非后续隐藏层）。我们希望能够找到全局最优的 $W^*$ 与 $b^*$ 。

首先，对于 $W^*$ 而言，这个问题能够等价转换为求解下图优化问题中的最优解：

图中的 $b^*$ 是一个定值。由于Slater条件成立，所以这个问题是强对偶的，也就是说，求它的对偶问题的最优解等价于求它的最优解。（Slater条件：在可行域内存在一个W，使得约束条件成立。但是为什么说这里Slater条件成立？）

像这样的情况，就可以使用KKT条件去求解了：

我们将原问题转化为求解：

其中， $s_j$ 是KKT乘子，我们对这个式子求梯度，满足以下KKT条件：

当 $s_j=0$ 时， $W_j^* = U_j-\overline{\lambda} v_j^*$ 。其中 $v_j^*$ 是 $|W_j^*|$ 的梯度，可以看作是示性函数 $sgn(W_j^*)$ ；这个方程求解出来的解便是软阈值函数 $W_j^*=S_{\overline{\lambda}}(U_j)$ (ISTA算法)；并且更具最下面的约束，它的绝对值应当小于 $M||b^*||_2$ 。

当 $s_j>0$ 时，根据KKT条件的第二个等式， $|W_j^*| = w=M||b^*||_2$ 。又根据第一个等式， $U_j = W_j^*+\overline{\lambda} v_j^*$ ，我们可以得出 $sgn(U_j)=sgn(W_j^*)$ ，进一步得出 $W_j^* = sgn(U_j)w$ 。倘若 $w!=0$ 那么由于 $W_j^* = U_j-(\overline{\lambda}+s_j)v_j^*= S_{\overline{\lambda}}(U_j)-s_jsgn(W_j^*)$ 我们能够得出它的约束： $|S_{\overline{\lambda}}(U_j)|>w$ 。

综上， $W^*$ 必须满足 $W^*_j = sgn(Uj)min{w,S_{\overline{\lambda}}(|U_j|)}$ 。

接下来就是找b的最优点了，这部分由于笔者的代数知识能力有限，这部分的转换并没有看懂，只是将论文中的证明贴在这里了：

将W看作是关于b的函数，则 $W_j(b)=sgn(Uj)min{M||b||_2,S_{\overline{\lambda}}(|U_j|)}$

于是我们就得到了关于b的函数：

$F(b)=\frac{1}{2}(||v-b||_2^2+||U-W(b)||_F^2)+\lambda||b||_2+\overline{\lambda}||W(b)||_1$

论文中将 ${|U_i|}$ 从大到小排列，当 $w=M||b||_2$ 属于 $[S_{\overline{\lambda}}(|U_{s+1}|),S_{\overline{\lambda}}(|U_{s}|))$ 时，我们有以下等式：

$F(b) = \frac{1}{2}(1+sM^2)||b-\frac{1}{1+sM^2}b||_2^2 + (\lambda-M\Sigma_{i=1}^s(|U_{(i)}|-\overline{\lambda}))||b||_2+r_s$

（这个式子是怎么化出来的我没看明白）

其中 $r_s$ 是与b无关的部分，我们将除了 $r_s$ 以外的部分看做与b相关的函数，则在 $F_s$ 处的全局最优点为

$b_s = \frac{1}{1+sM^2}(1-\frac{a_s}{||v||_2})_{+}v$

其中 $a_s = \lambda-M\Sigma_{i=1}^s(|U_{(i)}|-\overline{\lambda})$

（这里我依然没有看明白）

接下来的主要证明是 $s_*$ 是只有一个唯一值，且全局最优点正好是 $b_*=b_{s^*}$ 。此处笔者尚未理清他的思路，故而省略。

thorn_r

关注

20
点赞
踩
26

收藏

觉得还不错? 一键收藏
0
评论
机器学习论文及代码浅读：LassoNet

论文提出了一个在神经网络中能够做特征提取的结构：LassoNet，其核心思想，是使用一个“Skip层”的结构来控制要进入后面隐层的特征数量，从而实现特征的稀疏化。尽管原理看上去很简单，但是针对其进行反向传播的优化算法（Warm Start和Hier-Prox算法），实际上有着相当的数学最优化原理。这篇论文实际上结合了原本线性模型种的L1正则化与ResNet的思路，可以说有着借鉴价值。
复制链接

扫一扫