隐式马尔科夫链与维特比算法

1. 隐式马尔科夫链： 马尔科夫链是一系列的状态转换，设为x1...xn,其中xn至于xn-1相关，假设xi 会以p(i)的概率产生yi, 如下图所示：

 

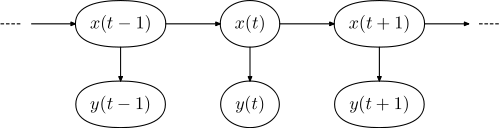
观察到的是Y的序列，由于X序列不可见，是隐式的，因此称为隐式马尔科夫链

 

真实系统中，x与y之间有可能不是一一对应的关系，但总有一个从X到Y的概率

 

现在我们观察到了一个Y的序列，要计算如下两件事情：

1. Y这个序列出现的概率多大？

2. 要出现Y这个序列，则概率最大的X序列是什么？

 

第一个问题:

假设X序列初始状态是Xi的概率为Ii, P(Xi|Xj) = Aij, P(Yi|Xi) = Bi

则Y序列的初始状态是Yi的概率为：P(Yi) =  Ii * Bi

P(Yi + 1) = sum(P(Xi + 1) | Xi) * Bi + 1

 

即，因此要计算序列Y1...Yn的概率，需要计算P(Xn | Y1...Yn-1),计算过程如下：

观察到事实Y1， 计算从状态Xi到所有其他状态在Xj这个事实下的转换概率，计算出在Y1这个事实下，所有X1...Xn的出现概率，依次如此计算，最后计算出Y1...Yn的概率

 

第二个问题：

由于马尔科夫链的关系，假设我们已经求出对应这Y1...Yi的最大概率X序列，那么对Yi +1, 我们只需计算Yi 到 Yi + 1的最大概率序列即可，即是从状态1到状态2的最大概率与状态2到状态3的最大概率无关。

 

举例如下：

例子来自于wiki：http://en.wikipedia.org/wiki/Viterbi_algorithm

#!/usr/bin/python #隐式马尔科夫链的后选事件集 states = ('Rainy', 'Sunny') #观察到的事件集 observations = ('walk', 'shop', 'clean') #后选事件集的初始概率 start_probability = {'Rainy': 0.6, 'Sunny': 0.4} #后选事件集的转换概率 transition_probability = { 'Rainy' : {'Rainy': 0.7, 'Sunny': 0.3}, 'Sunny' : {'Rainy': 0.4, 'Sunny': 0.6}, } #后选事件集到观察事件集的转换概率 emission_probability = { 'Rainy' : {'walk': 0.1, 'shop': 0.4, 'clean': 0.5}, 'Sunny' : {'walk': 0.6, 'shop': 0.3, 'clean': 0.1}, } def forward_viterbi(obs, states, start_p, trans_p, emit_p): T = {} for state in states: #初始化状态，T记录的是在观察事件序列发生的情况下，各个状态的概率 ## prob. V. path V. prob. T[state] = (start_p[state], [state], start_p[state]) for output in obs: U = {} for next_state in states: total = 0 argmax = None valmax = 0 for source_state in states: (prob, v_path, v_prob) = T[source_state] #计算在观察到的状态下，下一个后选状态，假设当前状态为rain，观察到的状态为walk,解释如下： #由于在rain的情况下walk的概率为0.1,因此可以认为rain的概率为0.1, 而在rain的情况下到下一个状态的概率为trans_p[source_state][next_state] #因此计算p，因此当前状态，在观察状态下，可以计算出所有下一个状态的概率，依次计算 p = emit_p[source_state][output] * trans_p[source_state][next_state] print output,source_state,next_state prob *= p v_prob *= p total += prob #计算最大概率路径 if v_prob > valmax: argmax = v_path + [next_state] valmax = v_prob U[next_state] = (total, argmax, valmax) T = U ## apply sum/max to the final states: total = 0 argmax = None valmax = 0 for state in states: (prob, v_path, v_prob) = T[state] total += prob if v_prob > valmax: argmax = v_path valmax = v_prob return (total, argmax, valmax) def example(): return forward_viterbi(observations, states, start_probability, transition_probability, emission_probability) print example()

 

网上还有一篇非常详细地介绍hmm的文章：

http://jedlik.phy.bme.hu/~gerjanos/HMM/node2.html#SECTION00200000000000000000