由于离学习数字图像处理已经有一段时间,之后一直涉及到的都是机器学习的内容。虽然期间也在做视频监控的项目,但是都是用别人现成的程序,并不涉及到图像的预处理和分析过程,我感觉到自己在图像方面的知识,仍有不足。趁此机会,对之前的学习课本,进行一次系统的整理。一来,熟悉图像处理的内容;二来,训练自己对书本内容的概括总结能力。
本来是打算参照贾永红版数字图像处理来写整个系列的,但是书里面这一章的内容,和我平时接触到的概念有出入。所以,这里我打算,按照自己的思路,整理本章。主要从傅里叶变换和小波变换2个变换入手,谈谈自己对冲激函数、采样定理、傅里叶变换以及小波变换的理解。
要点:
- 1.傅里叶变换与傅里叶逆变换
- 2.从连续、离散;周期、非周期方面讨论傅里叶变换
- 3.由傅里叶变换理解采样定理
- 4.唯一适用于计算机的傅里叶变换(DFT),如何处理?——循环卷积
- (其间,穿插着介绍一些必备知识,以及自己的一些思考)
一、傅里叶变换和傅里叶逆变换
在介绍“傅里叶变换”之前,我们先介绍2个概念:正交性和完备性。
(1)正交性
连续情况时,

离散情况时,
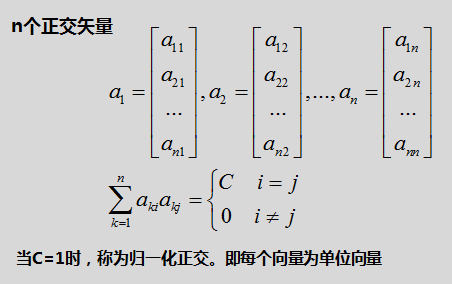
(2)完备性
介绍正交性和完备性,是为了引出“正交完备函数集”的概念:顾名思义,一组函数集,既满足两两正交,又具有完备性,那么则称这组函数集为正交完备函数集。
而三角函数集正好是一组正交完备函数集。(这里我们只给出三角函数正交性的结果;而三角函数的完备性证明较复杂,我们在此略过,记住这一结论就行)
在了解傅里叶变换之前,我们还有必要了解这么一个事实:
周期信号在它的一个周期内,可以展开成在完备正交函数空间中的无穷级数。如果完备的正交函数集是三角函数或指数函数集,那么周期信号所展开的无穷级数称为“傅立叶级数”。
所以,对于一个周期为T的函数f(t),角频率为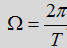
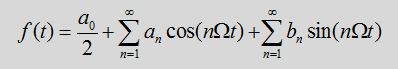
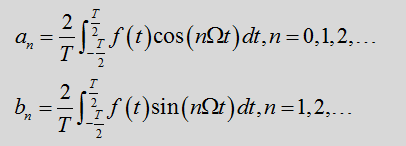
【求解推导如下所示:】
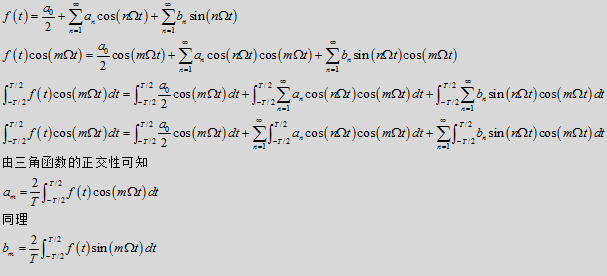
傅里叶级数合并同频率项表示为:
我们知道,三角函数和指数函数直接存在着某种联系,而且我们可以用欧拉公式来表示这一关系:
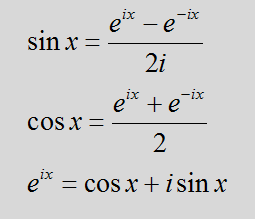
所以f(t)傅里叶级数可进一步表示为
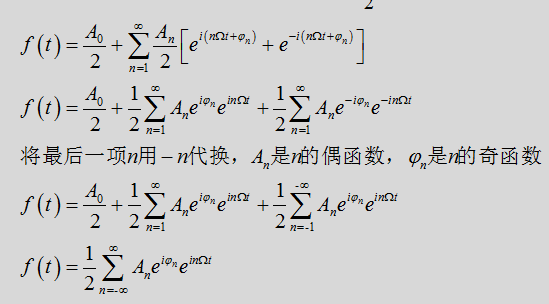
最后,得到傅里叶级数(展开)和傅里叶变换,结果为
由上式我们得到傅里叶展开结果,并且我们把第一个红框中的式子称为傅里叶逆变换或傅里叶展开;第二个红框中的式子称为傅里叶变换。
对于非周期函数f(t)而言,我们可认为其周期T无穷大。其傅里叶变换和逆变换分别为
傅里叶变换具有很多有用的性质:

这里我们仅给出卷积定理的证明(因为最重要):
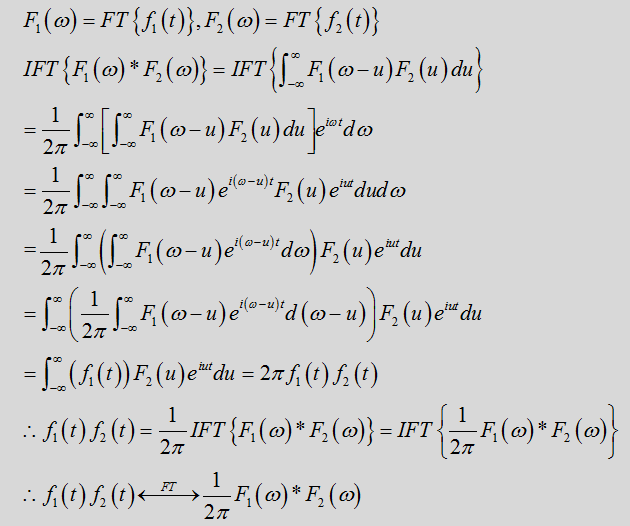
卷积定理出现,建立空间域和频率域之间的关系,它是图像处理中空间域和频率域之间的转换桥梁。
同样,我们可以将傅里叶变换拓展到二维连续信号,其傅里叶变换和逆变换为

而且,将傅里叶变换拓展到二维,使得它还具备在一维中不存在的特性:可分性和旋转性(若空间域函数旋转某一角度,则变换域中该函数的傅立叶变换函数也将旋转同样的角度)
二、讨论连续、非连续;周期、非周期配对组合的傅里叶变换
(1)首先,假设空间域中函数f(t)连续;
- 若f(t)为连续周期函数,其傅里叶变换及逆变换为
- 若f(t)为连续非周期函数,其傅里叶变换及逆变换为
(2)假设空间域中函数f(t)离散;
- 若f(t)为离散周期函数,其傅里叶变换及逆变换为
若f(t)为离散非周期函数,其傅里叶变换及逆变换为
对以上4种情况考虑,我们发现以下规律:
当函数f(t)为周期函数时,其傅里叶变换在频率轴上取值离散(只在
处取值);
- 当函数f(t)为非周期函数时,其傅里叶变换在频率轴上取值连续;
当函数f(t)为离散函数时,
(1)周期函数时,
(2)非周期函数时
无论f(t)是周期还是非周期函数,其傅里叶变换均为周期函数;当函数f(t)为连续函数时,由上述连续周期和连续非周期对应的F(
)和F(w)公式可知,F(
)和F(w)均为非周期函数。
所以,总结有如下对应关系:(无论空间域,还是频率域)均有
连续——非周期;离散——周期。
三、由傅里叶变换理解采样定理
插播:
之前一直没搞清采样、DTFT(Discrete-Time Fourier Transform)、DFT(Discrete Fourier Transform)之间的关系,在反复阅读相关材料后,终于领悟,下面用一张图来表示它们之间的关系:
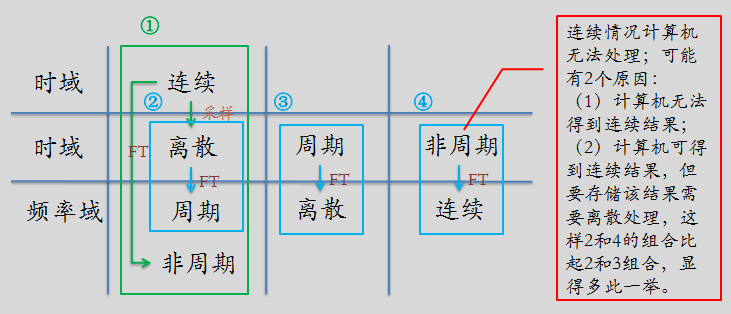
- 采样定理及采样分析:其研究的是方框1中的内容,即连续函数经采样变成离散函数(时间域乘积),以及连续函数经过傅里叶变换转到频率域进行分析(频率域卷积),确定无损信号的采样频率;
- DTFT则是方框2和方框4的组合分析;
- DFT是方框2和方框3的组合分析。
继续插播:冲激函数
什么是冲激函数,我们给出如下定义。

这样的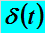
也可表示为:
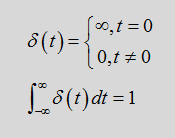
(现在在某些情况下也有用当t=0时,冲击函数的值取1,称单位冲击函数。在理解它的积分中比较好理解,而且目前大多数数字信号处理教材都采用值为1的形式) ——来自百度百科:说实话,这一部分没懂,不过这一取值有助于之后理解采样中连续函数与梳妆函数乘积
如图所示:
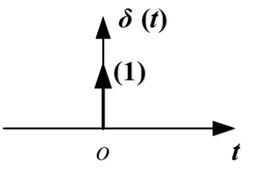
冲激函数具有筛选性和取样性:
(1)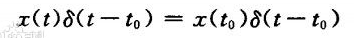
(2)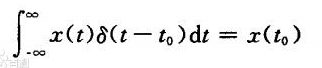
其中
- 性质(1)表明,信号x(t)与冲激函数相乘,筛选出连续时间信号x(t)在t=t0时的函数值x(t0)。可以理解为冲激函数在t=t0时刻对函数x(t)的一瞬间的作用,其值是冲激函数和x(t0)相乘的结果,瞬间趋于无穷大
- 性质(2)冲激信号的取样特性表明,一个连续时间信号x(t)与冲激函数相乘,并在(一∞,+∞)时间域上积分,其结果为信号x(t)在t=t0时的函数值x(t0)。该式可以理解为冲激函数作用于函数x(t),趋于稳态时最终作用的结果,即得到信号x(t)在t0时刻的值x(t0)
- (我认为,在信号处理中,取样性和筛选性其实是一个式子)
结合卷积定义有如下证明:
下面正式开讲“怎么由傅里叶变换理解采样定理”:
首先,这里我们抛出一个问题:假设我们有一个连续信号f(t),如下图所示,我们如何实现采样呢?
- 答案是:将连续函数与冲激函数串相乘
我们定义冲激函数串为梳妆函数,其图示及表达式如下图所示:
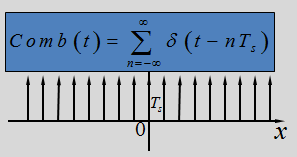
由冲激函数的筛选性,我们知道,通过与单位冲激函数相乘能够筛选出t=t0处函数f的值。(这里用“当t=0时,冲击函数的值取1”,更易理解)——至于为什么无穷大可以取作1,而不会与冲激函数定义产生矛盾,现在我还不太清楚,
所以当我们用梳妆函数与原连续函数fa(t)做乘积时,可得离散函数f(t),如下图示:
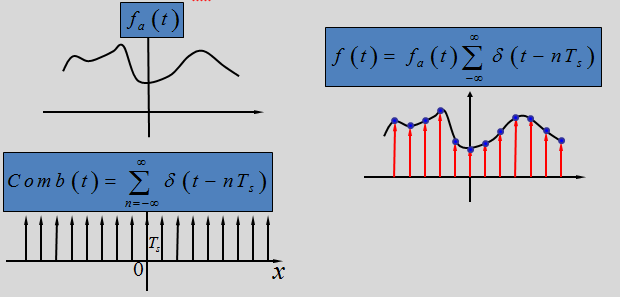
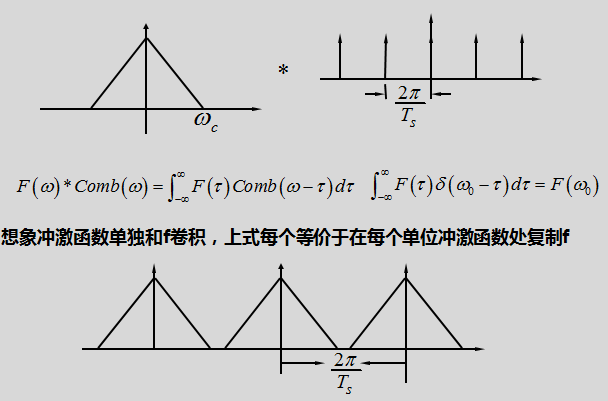
由卷积定理可知,时间域函数相乘,则对应于它们的傅里叶变换做卷积操作。所以,我们可以把采样操作(时间域中原函数与梳妆函数相乘)当做频率域函数的卷积来分析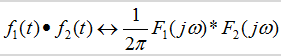
我们分别对原函数fa(t)和梳妆函数Comb(t)做傅里叶变换,得如下所示函数:
(由于原函数fa(t)为连续函数,其傅里叶变换为非周期函数,且自然界中事物一般都存在截止频率-我们令其为wc-所以fa(t)傅里叶变换可用上图表示)
在频率域中做卷积分析。。。
- (1)证明“冲激函数单独和F卷积,仍为F”
- 其实很简单,只要假设
,由冲激函数的取样性,我们可知
,所以原函数F与冲激函数的卷积函数仍为原函数
- (2)证明“上式等价于在每个单位冲激函数处复制F”
- 所以原函数F与梳妆函数卷积结果为周期函数,且每个周期内函数部分与F相同(由于F在
=(负无穷,正无穷)内,只存在一个周期(-wc,wc))
但是,上面是我们假设,才有“每个周期内函数部分与F相同”,若不满足
,则会出现以下情况:
所以,有以下结论:
如果要完全无损的从数字化的函数恢复原函数,必须保证
四、唯一适用于计算机的傅里叶变换(DFT),如何处理?——循环卷积
由于计算机只能处理“离散”情况的函数。所以在四种情况里,只有时域中离散、周期函数(其对于频率域中周期、离散函数)满足变换前后均为离散。所以唯一适用于计算机的傅里叶变换也就是讨论对原函数为离散、周期函数进行傅里叶变换的过程。
插播:循环卷积
假设有2个周期均为N的函数,分别记为x(n)和h(n),其循环卷积为
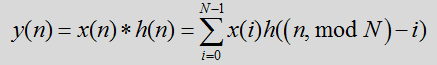
它与线性卷积不同之处是卷积过程只限在n=0到N-1的一个周期内。
【图示理解循环卷积】
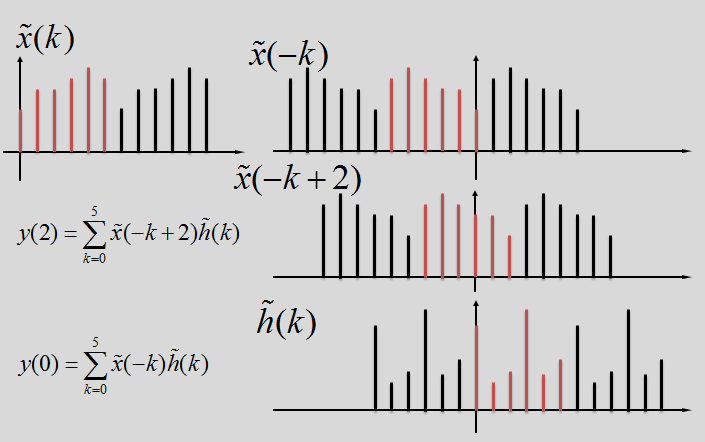
理解循环卷积:(注意,做循环卷积的2个函数周期一定要相等)
x(n),y(n),h(n)本质上都是周期函数的一个周期,在进行卷积运算时,整个周期函数都被翻转并移动,因此在一个固定周期内的运算会有移入和移出。
然而,在实际问题中,碰到的问题大多数是求解线性卷积,例如,一个LSI系统,输出y(n)为y(n)=x(n)*h(n)。
那么,我们是否可用循环卷积来求解线性卷积呢?(准确来说,应该是“是否用两个周期函数的循环卷积来求解这两个周期函数对应某一周期内序列段的线性卷积”——“有点拗口”)
下面我们来做进一步的解释:
设 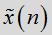
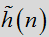
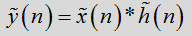
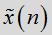
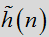
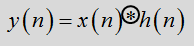
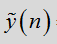
答案是:肯定的。采用的方法是补零展宽,展宽后序列x(n),h(n)周期均为>=N+M-1。这里我们不严格证明,而是采用图解的方式进行说明。
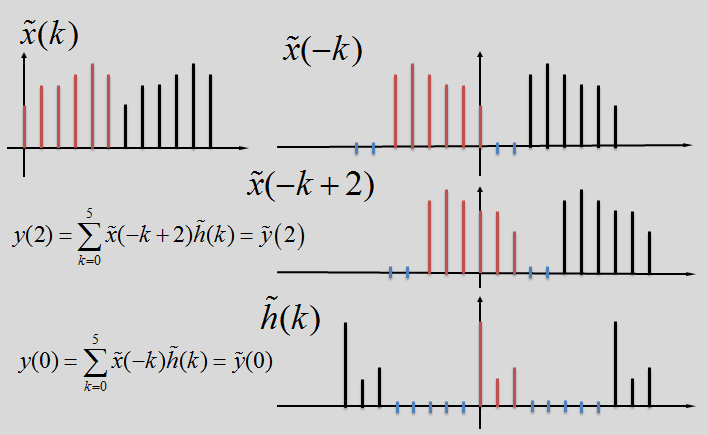
上图中,当x(n)和h(n)补零展宽到N+M-1时,做循环卷积时,信号没有发生混叠,其循环卷积结果等于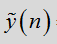
我们考虑当x(n)和h(n)补零展宽小于N+M-1时,会发生什么情况:
如上图所示,信号会发生混叠,x(n)和h(n)的循环卷积无法用于求解
上面我们也提到:卷积定理的出现,建立了空间域和频率域之间的关系,它是图像处理中空间域和频率域之间的转换桥梁。
由于DFT对应时域和频率域函数是离散周期函数,故其满足的是循环卷积定理。(注:我们最后真正需要的是离散周期函数的一个周期内的线性卷积,这也是我们之前讨论循环卷积和线性卷积关系的原因)
下面让我们来对离散周期函数的循环卷积定理进行证明。
循环卷积定理:
(讨论离散周期函数)
由第二部分内容我们知道,离散周期函数的傅里叶变换及傅里叶逆变换的公式为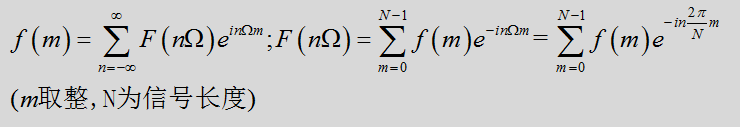
这里我们给这两个式子取个名字:前者我们称为IDFT(离散傅里叶逆变换);后者我们称为DFT(离散傅里叶变换)
我们假设有2个时域上的离散周期函数x(n),h(n),其周期均为N。根据循环卷积定义,我们可以求出x(n)与h(n)的卷积y(n)。下面我们对y(n)进行离散傅里叶变换(这里我们不妨令n属于(0,N-1)),可得
到这,傅里叶变换的介绍也就结束啦。上面我们介绍了傅里叶变换的三角函数形式、指数形式;傅里叶变换中时域、频率域中连续与周期的对应关系;从傅里叶变换来理解采样定理以及最后我们为了在计算机中使用傅里叶变换而采用离散周期函数。
最后让我们用一张图来介绍一下DFT被提出的历程吧。
关于傅里叶变换的一些思考:
(1)数字图像处理中为什么说高斯函数是低通滤波器?
答:首先我们要知道空间域中高斯函数经过傅里叶变换后仍是高斯函数。一般我们在图像处理中采用的高斯函数都是均值为0的滤波器,如图所示。(这里我们用一维示例)
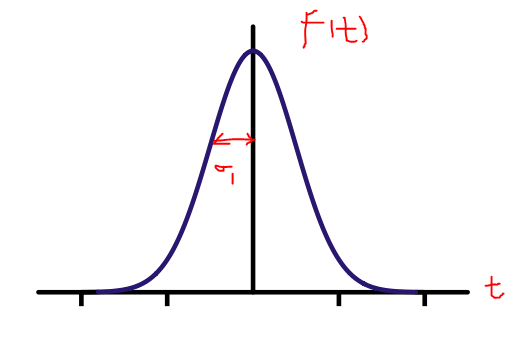
其对应频率域函数为
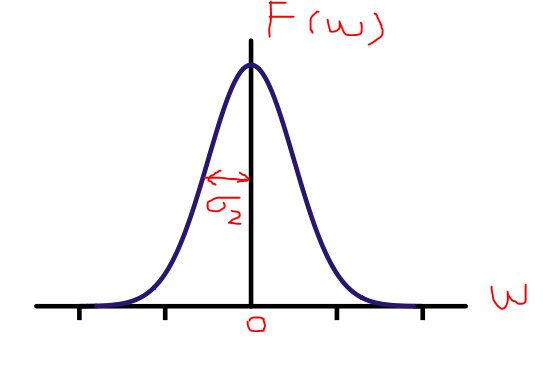
从频率中我们看到,高频部分权重很小,而低频部分权重很大,故高斯函数为低通滤波器。
后记:本文主要是我根据老师上课所用PPT进行整理,由于有些是自己思考的结果,可能会有理解不到位的地方。请大家匹配指正。













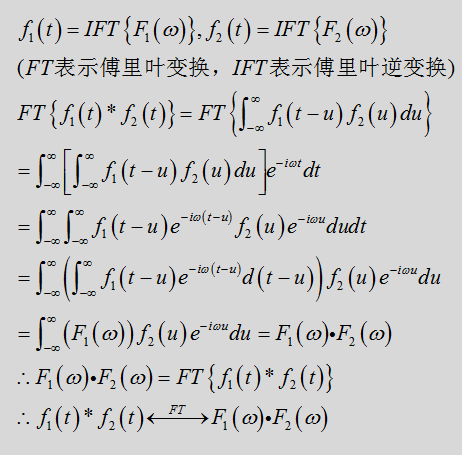

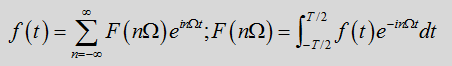
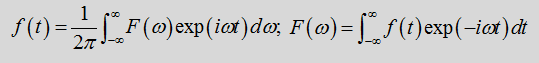
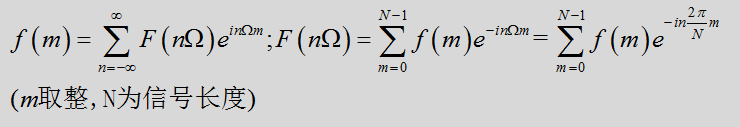
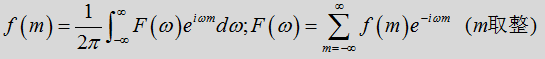
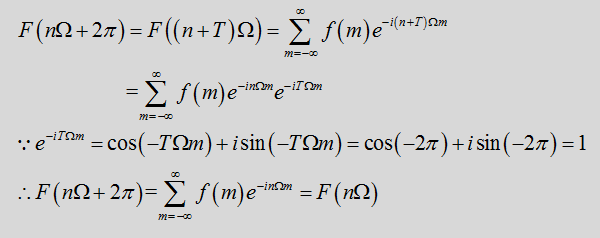
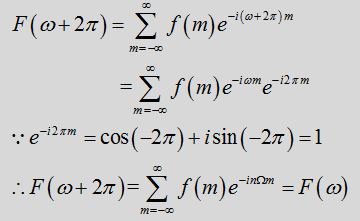
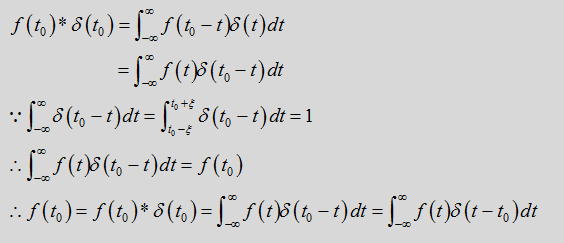

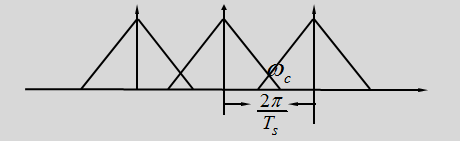



















 2714
2714

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










