接地气讲解决策树算法的原理

来源：机器学习杂货店‍‍‍‍‍
本文约1300字，建议阅读7分钟
本文为你介绍决策树算法的原理。

❝

决策树（）是一类很常见很经典的机器学习算法，既可以作为分类算法也可以作为回归算法。同时也适合许多集成算法，如, ，以后会逐一介绍。本篇介绍一下决策树算法的原理。❞

决策树算法不像前面介绍的SVM那样，散发着浓厚的数学气味。这个算法还是比较接地气的。

信息论基础

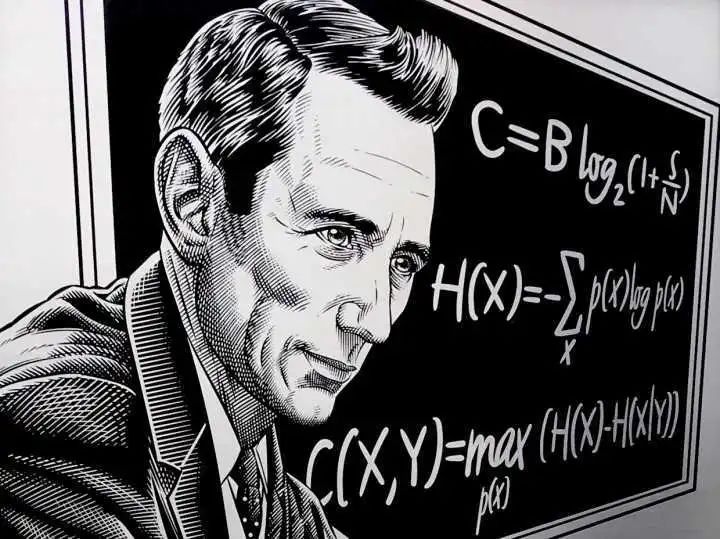 这个语法结构大家应该不陌生。怎样准确地定量选择  后面的条件，也就是要找到一个性能指标来衡量这个条件的好坏。（就像SVM中引入了来衡量一条直线的好坏）。

70年代，一个名为昆兰的大牛找到了信息论中的「熵」来度量决策树的决策选择过程。注意，信息论中的熵是香农提出的。昆兰只是将熵应用于决策树的人。

熵度量了事物的不确定性(可以联想化学里的熵，混乱程度)，越不确定的事物，它的熵就越大。具体的，随机变量X的熵的表达式如下：

决策树构造

决策树的组成：

1. 根节点：第一个选择点

2. 非叶子节点与分支：中间过程

3. 叶子节点：最终的决策结果

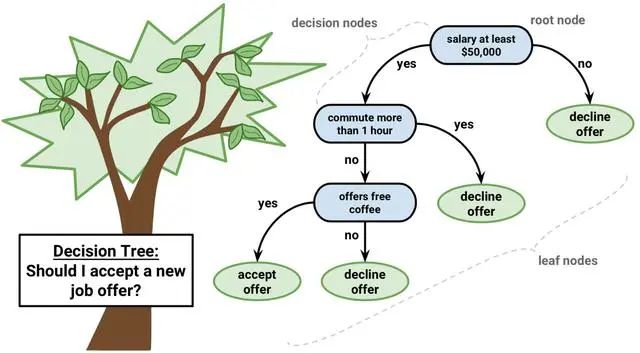就像这张图展示的，第一个节点就是根节点，绿色的代表  也就是叶子节点，其它的节点也就是非叶子节点(用于决策)，也就是 。

那么如何构造决策树呢？

「第一步，选择根节点」。

问题来了，特征不唯一，选哪一个作根节点最优？

这就涉及到了衡量标准，一般而言，随着划分过程不断进行，我们希望节点的熵能够迅速地降低。因为随机变量的熵越大，随机变量的不确定性越大，代表纯度越低。所以希望节点的熵能够迅速降低，使得纯度不断增加。所以以「信息增益」作为衡量标准。

引入一个信息增益( )的概念。

❝

「定义」：特征  对训练数据集  的信息增益 ，定义为集合  的经验熵  与特征  给定条件下  的经验条件熵 之差，即

❞

信息增益也就度量了熵降低的程度。以信息增益作为衡量标准的算法被称为ID3算法。

「第二步，选择子节点」。

依然是采用信息增益的标准进行选择。

「第三步，何时停止」。

其实这一步就涉及到剪枝，下文详解。

如果对这些概念还是有点模糊，可以结合下面的实例再思考思考。

实例

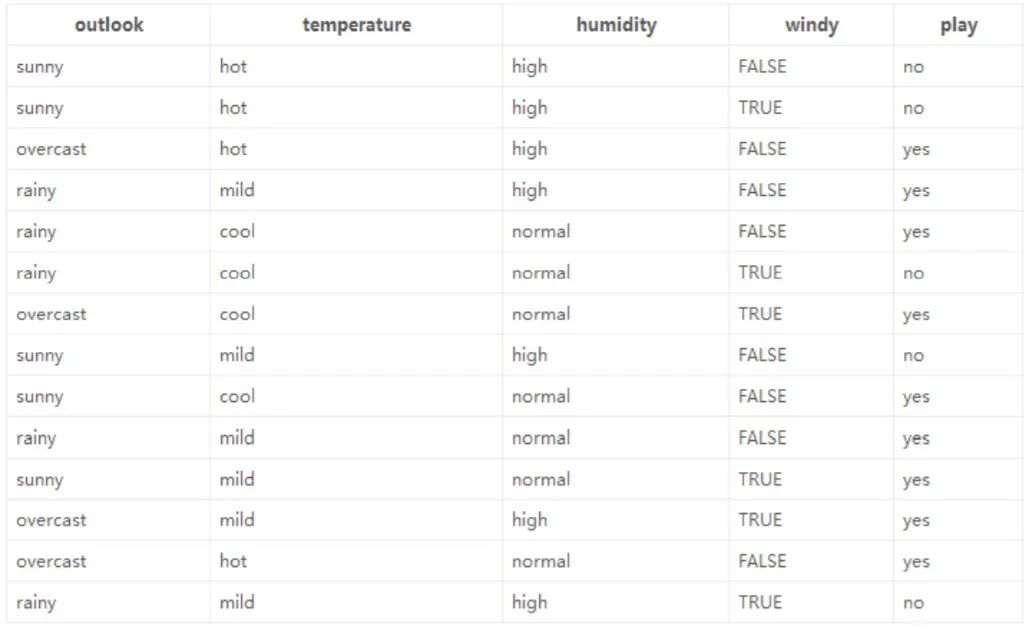这是数据（14天的打球情况），有四种环境特征（outlook,humidity）,最后一列(play）代表最后有没有出去打球。

「首先，选择根节点」。一共有四个特征，所以根节点的选择有四种。

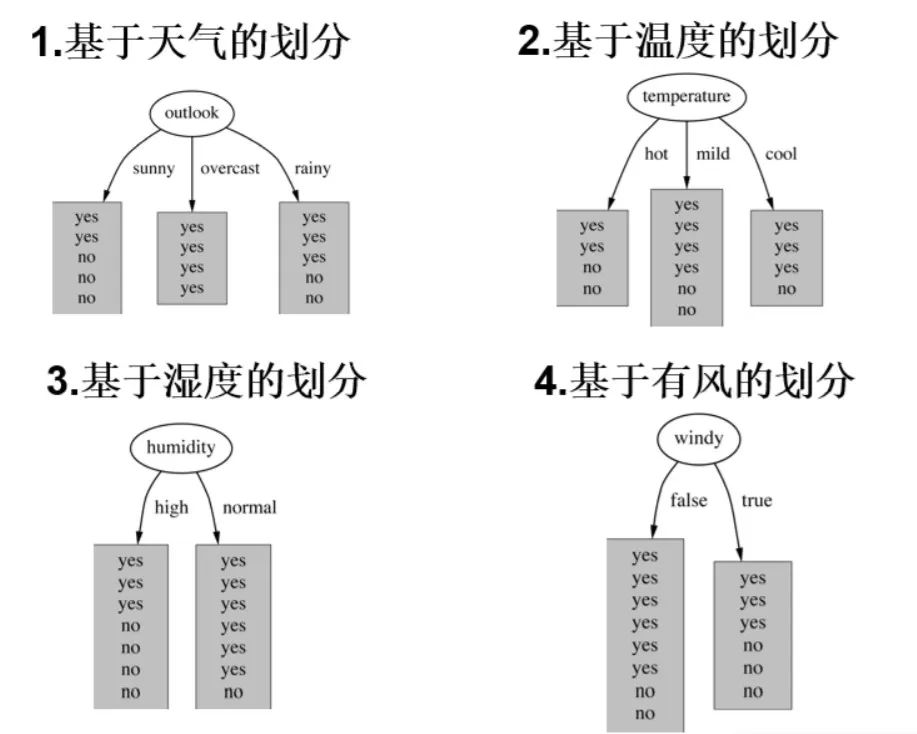
在我们的原始数据（14天）有9天打球，5天不大，所以此时的熵为：

接着，四个特征逐一分析，先从(天气)下手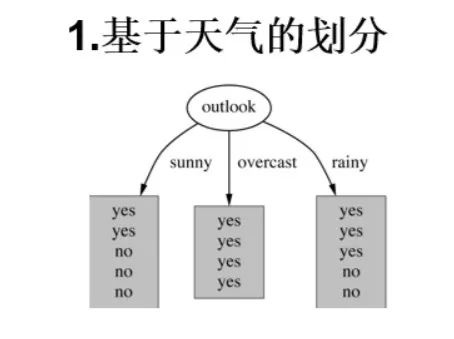：当  时，当  时，当  时，

根据数据， 取 ,,的概率分别为,熵值计算（几个特征属性熵的加权求和）：

信息增益：

同样的方式计算其它三个特征的信息增益：

四个特征中， 的增益最大，所以选择作为根节点。「接下来的子节点选择同上」。

「何时停止？」上文也说了，"何时停止"涉及到剪枝。为什么要剪枝？决策树存在较大的过拟合风险，理论上，决策树可以将样本数据完全分开，但是这样就带来了非常大的过拟合风险，使得模型的泛化能力极差。

剪枝和日常树木的修建是一个道理。这里介绍最常用的「预剪枝」，在构造决策树的过程中，提前停止。具体的预剪枝策略有：

• 限制深度，例如，只构造到两层就停止。

• 限制叶子节点个数，例如，叶子节点个数超过某个阈值就停止等等。

Ensemble Learning  

简单介绍一下集成学习（）。有两种类型，

1. Bagging ：训练多个分类器，最后可采取投票机制选择最终结果。这里的分类器常常是决策树。代表算法是 

2. Boosting：仍是训练多个分类器，将最后的结果加权求和，代表算法是,

这些算法在一些比赛中都是很常见的。

本篇主要介绍的ID3算法仍有一定缺陷，之后的文章会继续介绍。

编辑：tech小百科

参考目录：

https://www.bilibili.com/video/BV1Ps411V7px?p=6

https://www.cnblogs.com/pinard/p/6050306.html

https://divinerhjf.github.io/2019/05/24/shu-ju-wa-jue-jue-ce-shu/#toc-heading-8

https://zh.wikipedia.org/wiki/‍‍‍

编辑：黄继彦