【C++研发面试笔记】9. 基本数据结构-二叉查找树BST

【C++研发面试笔记】9. 基本数据结构-二叉查找树BST

BST树即二叉搜索树，其满足如下条件：
1.所有非叶子结点至多拥有两个儿子（Left和Right）；
2.所有结点存储一个关键字；
3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

9.1 BST树的搜索

• 从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；
• 否则如果查询关键字比结点关键字小，就进入左儿子；
• 如果比结点关键字大，就进入右儿子；
• 如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；

如果BST树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么B树的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变BST树结构（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；
同样的关键字集合有可能导致不同的树结构索引；所以，使用BST树还要考虑尽可能让BST树保持左图的结构，和避免右图的结构，也就是所谓的“平衡”问题；

---

9.2 BST的建立

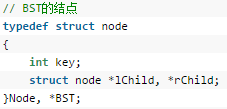
9.2.1 结构

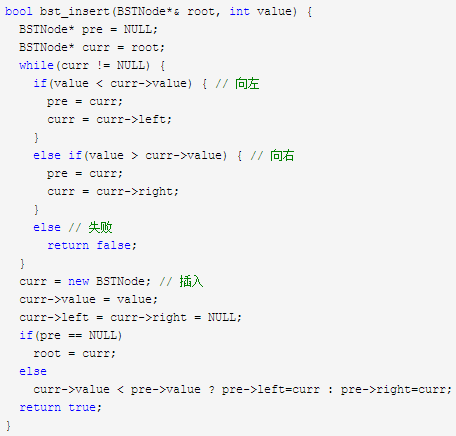
9.2.2 插入

递归方法：

9.2.3 构建

9.2.4 查找

递归方法：

先序遍历

中序遍历

9.2.5 删除节点

删除操作也类似于查找，是个递归过程，只不过删除操作在找到被删除节点后的处理要复杂些，需考虑下面4种情形：

1. 当前节点的关键值等于待删除关键值，则进入删除处理过程；
2. 当前节点的关键值小于待插入节点关键值，根据BST的定义，应在当前节点的左子树上递归删除操作；
3. 当前节点的关键值大于待插入节点关键值，根据BST的定义，应在当前节点的右子树上递归删除操作；
4. 若当前节点为空，则说明查找不到待删除关键值的节点，返回-1指示删除失败。

删除处理过程又需要考虑以前几种情形：

1. 待删除节点为叶子节点（左右孩子均为空）；
   a) 将待删除节点的父节点指向该待删除节点的指针置为空，
   b) 删除待删除节点。
2. 待删除节点的左孩子为空，右孩子非空；
   a) 将待删除节点的父节点重新指向待删除节点的右孩子
   b) 删除待删除节点。
3. 待删除节点的左孩子非空，右孩子为空；
   a) 将待删除节点的父节点重新指向待删除节点的左孩子
   b) 删除待删除节点
4. 待删除节点的左孩子非空，右孩子非空。
   a) 将待删除节点的关键值与其右子树上值最小节点的值交换
   b) 也可以选择待删除节点左子树上的最大值节点进行交换

这篇博文是个人的学习笔记，内容许多来源于网络（包括CSDN、博客园及百度百科等），博主主要做了微不足道的整理工作。由于在做笔记的时候没有注明来源，所以如果有作者看到上述文字中有自己的原创内容，请私信本人修改或注明来源，非常感谢>_<