机器学习模型相关评价指标最全总结

机器学习模型评价指标总结

1. 混淆矩阵（Confusion Matrix）

（以下先考虑二分类问题）

其中：  TP（实际为正预测为正），FP（实际为负但预测为正）

TN（实际为负预测为负），FN（实际为正但预测为负）

2. 基于混淆矩阵的相关评价指标

  A．召回率：Recall = TP / (TP+FN)  

（又称查全率，反映预测对的正例数占真正的正例数的比率）

  B．准确率：Accuracy = (TP+TN) / (TP+FP+TN+FN) 

（反映分类器对整个样本的判定能力，能将正的判定为正，负的判定为负）

  C．查准率：Precision=TP / (TP+FP)

      （指所得数值与真实值之间的精确程度；预测正确的正例数占预测为正例总量的比率）

  D． F值： F1-score = (2Recall*Precision) / (Recall + Precision)

      （F-score是Precision和Recall加权调和平均数，F1-score为F值一般公式中β=1的情况（即Precision和Recall同等重要，若β>1则Recall有更大影响），很多信息检索系统、分类、推荐系统的评测指标就是用F值）

3. ROC图、PR图以及AUC

（1） ROC图

  在混淆矩阵中，真正率 TPR = TP / (TP+FN)，假正率  FPR = FP / (FP + TN)

其中TPR也即灵敏度（sensitivity），FPR也即(1-特异度)（specificity）。以纵坐标为TPR，横坐标为FPR，ROC 曲线实际就是不同阈值下TPR和FPR的轨迹。每一个预测结果在ROC空间中以一个点代表。

阈值：阈值就是一个分界线，用于判定正负例的，在模型预测后我们会给每条预测数据进行打分（0<score<1）。如：指定阈值为0.6，那么评分低于0.6的会被判定为负例（不好的），评分高于0.6的即会判定为正例（好的），随着阈值的减小，判定为正例的样本相应地就会增加。

最好的预测方式是一个在左上角的点，在ROC空间坐标轴(0,1)点，这个代表着100%灵敏（没有假阴性）和100%特异（没有假阳性）。而(0,1)点被称为“完美分类器”。一个完全随机的预测会得到一条从左下到右上对角线（也叫无识别率线）上的一个点，这条线上的任一点对应的准确率（Accuracy）都是50%。

                                                                                    ROC图

     离散分类器，如决策树，产生的是离散的数值或者一个二元标签。应用到实例中，这样的分类器最后只会在ROC空间产生单一的点。而一些其他的分类器，如朴素贝叶斯分类器，逻辑回归或者人工神经网络，产生的是实例属于某一类的可能性，对于这些方法，一个阈值就决定了ROC空间中点的位置。举例来说，如果可能值低于或者等于0.8这个阈值就将其认为是阳性的类，而其他的值被认为是阴性类。这样就可以通过画每一个阈值的ROC点来生成一个生成一条曲线。

（2） PR图

P-R曲线的P就是查准率（Precision），R就是查全率（Recall）。用P作为横坐标，R作为纵坐标，就可以画出P-R曲线。

对于分类器，通过调整分类阈值，可以得到不同的P-R值，从而可以得到一条曲线（纵坐标为P，横坐标为R）。通常随着分类阈值从大到小变化（大于阈值认为P），Precision减小，Recall增加。比较两个分类器好坏时，显然是查得又准又全的比较好，也就是的PR曲线越往坐标（1，1）的位置靠近越好。 

  

                                                                                                  PR图

（3） AUC

AUC（Area Under the ROC Curve）指标在模型评估阶段常被用作最重要的评估指标来衡量模型的准确性。AUC作为模型评价指标，用于二分类模型的评价。 

AUC值是一个概率值，当你随机挑选一个正样本以及负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值，AUC值越大，当前分类算法越有可能将正样本排在负样本前面，从而能够更好地分类。
  为什么要用AUC作为二分类模型的评价指标呢？为什么不直接通过计算准确率来对模型进行评价呢？答案是这样的：机器学习中的很多模型对于分类问题的预测结果大多是概率，即属于某个类别的概率，如果计算准确率的话，就要把概率转化为类别，这就需要设定一个阈值，概率大于某个阈值的属于一类，概率小于某个阈值的属于另一类，而阈值的设定直接影响了准确率的计算。

ROC曲线与X坐标轴所围成的面积即为ROC-AUC值，AUC值越接近1模型的效果越好。横坐标为其中随机分类的模型AUC为0.5，所以模型的AUC基线值大于0.5才有意义。模型的ROC曲线越远离对角线，说明模型效果越好。随着阈值的减小，Sensitivity（ TPR）和1-Specificity（ FPR）也相应增加，所以ROC曲线呈递增态势。而PR曲线与X坐标轴所围成的面积即为PR-AUC值。

（4） ROC与PR的关系

ROC对应的指标是： a. TPR 正样本预测准确率（就是查全率Recall），评价的是模型在正样本集合上的表现。 b. FPR，负样本预测错误率。评价的是模型在负样本集合上的表现。

PRC对应的指标是： a. 查全率Recall（同ROC的TPR） b. 准确率P，所有预测样本的准确率（包括正样本和负样本）。最关键的就是这个，其他两个都是单独评价正样本集合或者负样本集合的。只有它是综合评价整体结果。所以，哪种类型（正或者负）样本多，权重就大。也就是通常说的对样本不均衡敏感

ROC曲线是FPR和TPR的点连成的线，PR曲线是查准率和查全率的点连成的线。又Recall=TPR，因此PR的横坐标为ROC的纵坐标。TPR、Recall的分母为样本中正样本的个数，FPR的分母为样本中负样本的个数，样本一旦确定分母即为定值。但是Precision的分母为预测为正样本的个数，会随着阈值的变化而变化，因此Precision的变化受TP和FP的综合影响，不单调，变化情况不可预测。

因此，相对来讲ROC曲线会更稳定，在正负样本量都足够的情况下，ROC曲线足够反映模型的判断能力。而在正负样本分布得极不均匀(highly skewed datasets)的情况下（正样本极少），PRC比ROC能更有效地反映分类器对于整体分类情况的好坏。总之，只画一个曲线时，如果没有data imbalance,倾向于用ROC（更简洁，更好理解）。如果数据样本不均衡,分两种情况：情况1：如正样本远小于负样本，PRC更敏感，因为用到了precision=(TP/(TP+FP))。情况2：正样本远大于负样本，PRC和ROC差别不大，都不敏感。

对于同一模型，PRC和ROC曲线都可以说明一定的问题，而且二者有一定的相关性，如果想评测模型效果，也可以把两条曲线都画出来综合评价。

4. Lift提升图、Gain增益图与K-S图

  （1） Lift提升图

   Lift =[TP/(TP+FP)] / [(TP+FN)/(TP+FP+FN+TN)] = Precision / Accuracy，它衡量的是，与不利用模型相比，模型的预测能力“变好”了多少，lift(提升指数)越大，模型的运行效果越好。Lift图分累积的和非累积的。

不利用模型，我们只能利用“正例的比例是(TP+FN)/(TP+FP+FN+TN)”这个样本信息来估计正例的比例（baseline model），而利用模型之后，我们不需要从整个样本中来挑选正例，只需要从我们预测为正例的那个样本的子集TP+FP中挑选正例，这时预测的准确率 (Precision)为TP/(TP+FP)。

（2） Gain增益图

Gini系数也可用于评价模型，Gains(增益) 与 Lift（提升）类似：Lift 曲线是不同阈值下Lift（Precision / Accuracy）和Depth的轨迹，Gain曲线则是不同阈值下Precision和Depth的轨迹，而Precision = TP/TP+FP，所以它们显而易见的区别就在于纵轴刻度的不同。（注：横轴Depth也就是：将样本的预测为1的概率从大到小排序后，取前百分之几。）

Gain增益图是描述整体精准率的指标。按照模型预测出的概率从高到低排列，将每一个百分位数内的精准率指标标注在图形区域内，就形成了非累积的增益图。如果对每一个百分位及其之前的精准率求和，并将值标注在图形区域内，则形成累积的增益图。累积图通常能够更好的表现模型性能，而非累积图则更有利于指出模型中可能存在问题的地方。

（3） K-S图

在评价模型时还会用到KS（Kolmogorov-Smirnov）值，KS=max(TPR-FPR)，即为TPR与FPR的差的最大值，KS值可以反映模型的最优区分效果，此时所取的阈值一般作为定义好坏用户的最优阈值。一般，KS>0.2即可认为模型有比较好的预测准确性。

  K-S曲线的最高点（最大值）为KS值，KS值越大，模型分值的区分度越好，KS值为0代表是最没有区分度的随机模型。准确的来说，K-S是用来度量正样本与负样本区分程度的。但KS值所代表的仅仅是模型的分隔能力，并不代表分隔的样本是准确的。换句话说，正负样本完全分错，但KS值可以依旧很高。

                                                                                                    K-S图

ROC曲线和lift曲线、Gain曲线、KS图都能够评价模型的效果，lift曲线/Gain曲线评价模型的有效性，其为总体一部分上的模型性能，而混淆矩阵评估的是整个总体上的模型性能。

  类似信用评分的场景，希望能够尽可能完全地识别出有违约风险的客户，选择ROC曲线及相应的AUC或者KS值作为指标；而类似数据库精确营销的场景，希望能够通过对全体消费者的分类而得到具有较高响应率的客户群从而提高投入产出比，选择lift曲线/Gain曲线作为指标。

上面四种曲线以预测客户是否违约的案例比较如下：

5. 回归模型的评价指标

回归模型常见应用：市场趋势报告、气温预测、投资风险分析

（1）MAE（Mean Absolute Error）平均绝对差值

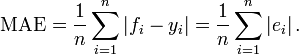
（2）MSE(Mean Square Error)均方误差，是回归任务最常用的性能度量

（3）log对数损失函数（逻辑回归）

（4）RMSE(Root Mean Square error)均方根误差

（5）Normalized root-mean-square deviation归一化均方差跟偏差

（6）  R2决定系数

        R2 是多元回归中的回归平方和占总平方和的比例,它是度量多元回归方程中拟合程度的一个统计量,反映了在因变量y的变差中被估计的回归方程所解释的比例。 
      R2 越接近1,表明回归平方和占总平方和的比例越大,回归线与各观测点越接近,用x的变化来解释y值变差的部分就越多,回归的拟合程度就越好

（7） Pearson's Correlation Coefficient(皮尔逊相关系数)

皮尔逊相关也称为积差相关（或积矩相关），假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：

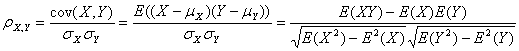
注意当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

•  两个变量之间是线性关系，都是连续数据。
•  两个变量的总体是正态分布，或接近正态的单峰分布。

③ 两个变量的观测值是成对的，每对观测值之间相互独立。

（8） concordance correlation coefficient(一致性相关系数)