多臂老虎机UCB1算法推导

多臂老虎机UCB1算法及其推导证明

UCB1算法是多臂老虎机问题中很简单也很经典的算法。
这里参考原始论文 “Finite-time Analysis of the Multiarmed Bandit Problem” 过一遍UCB1算法的推导过程。

---

1.多臂老虎机问题定义

  对一个$K$臂老虎机，随机变量$X_{i,n},1\le i\le K,n\ge 1$表示第$i$个臂在第$n$个回合产生的奖励值，第$i$个臂的奖励期望用${\mu }_i$表示，即 $IE[X_{i,n}]={\mu }_i$ , $IE[\cdot ]$表示求期望。每个臂在每个回合产生的奖励都是独立的。

  策略$A$表示如何根据过去的动作和获得的收益来选择下一轮执行的臂。我们用$T_i(n)$表示根据策略$A$，第$i$个臂在前$n$轮中被选择的次数。我们将策略$A$的遗憾值定义如下：
$${\mu }^{\ast }n-\sum _{j=1}^K{\mu }_j\ast IE[T_j(n)],where{\mu }^{\ast }\stackrel{def}{=}\underset{1\le i\le K}{\max }{\mu }_i(1)$$
所以遗憾值表示的是最优策略带来的收益和当前策略带来的收益之差。而这里的最优策略是已知每个臂的奖励分布情况下，每个回合中都一直选择收益最高的臂。

2.UCB1算法介绍

UCB1算法流程：

1. Initialization：每个臂各选择一次；
2. Loop：在第$n$个回合之后，也就是第$n+1$个回合进行决策时，选择能够最大化指标${\bar{x}}_j+\sqrt{\frac{2\mathrm{l}\mathrm{n}n}{n_j}}$的第$j$个臂，其中${\bar{x}}_j$表示第$j$个臂在过去的平均收益，而$n_j$表示第j个臂在过去$n$个回合中被执行的次数。

  算法流程很简单，而且有如下收敛性保证：对于任何$K>1$，如果这$K$个臂的奖励分布$P_1,P_2,...,P_K$被约束在$[0,1]$内，且${\mu }_1,{\mu }_2,...,{\mu }_K$分别是分布$P_1,P_2,...,P_K$的期望，那么在$n$个回合之后，UCB1策略的遗憾的期望值最多不会超过：
$$8\ast \sum _{i:{\mu }_i<{\mu }^{\ast }}(\frac{\mathrm{l}\mathrm{n}n}{{\Delta }_i})+(1+\frac{{\pi }^2}{3})(\sum _{j=1}^K{\Delta }_j)(2)$$
上式中：${\Delta }_i\stackrel{def}{=}{\mu }^{\ast }-{\mu }_i$，可以看出，上式第二项是和n无关的常量，而第一项也只是随着n呈O(ln(n))的增长。

3.UCB1算法证明推导

  对所有的$1\le i\le K,n\ge 1$我们定义：
$${\bar{X}}_{i,n}=\frac{1}{n}\sum _{t=1}^n{X}_{i,t}(3)$$
  假设我们知道哪个臂的奖励期望最高，在表示上，我们用$\ast$号来替代这个臂的编号，比如用${\mu }^{\ast }$来替代${\mu }_i$，用$T^{\ast }(n)$替代$T_i(n)$，用${\bar{X}}_n^{\ast }$来替代${\bar{X}}_{i,n}$。

   因为有 ${\sum }_{i=1}^K{T}_i(n)=n$，我们可以将（1）式中的遗憾值的期望写为如下：
$$\sum _{j:{\mu }_j<{\mu }^{\ast }}{\Delta }_j\ast IE[T_j(n)](4)$$
从式(4)可以看出，我们可通过限制住非最优臂被选择的次数，来限制住遗憾值。


  然后文章引入了两个定理：

第一个定理是chernoff-Hoeffding不等式，给出了具有边界范围的随机变量的和与其期望的偏差的上限，其中条件期望说明随机变量之间可以具有一定相关性，我们这里假设这些随机变量都是独立的。感兴趣可以参考如下资料：
Hoeffding不等式论文
Hoeffding不等式的讲义
机器学习数学原理（8）——霍夫丁不等式
第二个不等式为Bernstein不等式，在本次证明过程中并没有用到。相对于Hoeffding不等式考虑了方差的信息，如果方差较小能够获得比Hoeffding更紧的偏差上限，获得更精细的结果。可以参考：
Concentration Inequality(集中不等式)更新版
Bernstein不等式-维基百科


回到对UCB1的证明上来：
  我们定义$I_t$为第$t$轮选择的臂的编号，令变量$c_{t,s}=\sqrt{(2\mathrm{l}\mathrm{n}t)/s}$ ，$l$为一个人为设定的正整数，文章对$T_i(n)$给出了如下的上界：

对上面推导的说明：
第1个等式，直接利用了关于 $T_i(n)$ 的定义，因为第 $1-K$ 个回合会将 $K$ 个臂个执行一次；

第2个不等式，在 $l=1$ 时取等。不等式右侧在 $T_i(n)$ 小于 $l$ 的时候取 $l$，否则就取 $T_i(n)$;

第3个不等式，利用了UCB1的定义，即第 $t$ 回合选择第$i$个臂，必须满足第$i$个臂的UCB1的指标大于最优的臂的指标。这里 ${\bar{X}}_{i,T_i(t-1)}$ 表示的是第 $i$ 个臂在过去 $t-1$ 个回合中被选择后产生的奖励的均值，而 ${\bar{X}}_{T_i(t-1)}^{\ast }$ 表示的是最优的臂在过去 $t-1$ 个回合被选择后产生的奖励的均值，而其中的 $c_{t-1,T^{\ast }(t-1)},c_{t-1,T_i(t-1)}$ 就是UCB1公式中的第二项。为什么是小于等于呢？因为第 $i$ 个臂不仅需要和最优的比，还需要和其他的比。

第4个不等式，进一步放宽了条件，最优臂在被允许的选择次数下的最小指标 $<$ 第 $i$ 个臂在被允许的选择次数下的最大的指标。 （这里的均值 ${\bar{X}}_s^{\ast },{\bar{X}}_{i,s_i}$ 是怎么求的呢？？？）

第5个不等式，进一步放宽了约束，$t$ 从 $[K+1,n]$ 放宽到 $[1,\infty ]$ ，而对 $s,s_i$ 也从原来定义域里的最小最大这样一对比较，放宽到所有可能的比较。


上面给出了前n次第i个臂被执行次数的很宽的一个上界，下面到精彩的地方了：
如果希望 ${\bar{X}}_s^{\ast }+c_{t,s}\le {\bar{X}}_{i,s_i}+c_{t,s_i}$，下面三个条件至少有一个必须满足：

怎么理解：如何上面三个不等式全部都不满足，就会有：
$${\bar{X}}_s^{\ast }+c_{t,s}>{\mu }^{\ast }\ge {\mu }_i+2c_{t,s_i}>{\bar{X}}_{i,s_i}+c_{t,s_i}$$
而上面式(7)条件成立的概率可以通过Hoeffding不等式约束：\bar
I P { X ˉ s ∗ ≤ μ ∗ − c t , s } = I P { s X ˉ s ∗ ≤ s μ ∗ − s c t , s } ≤ e − 2 ( s c t , s ) 2 / s = e − 4 l n t = t − 4 IP\{\bar{X}^*_s\le \mu^*-c_{t,s}\}=IP\{s\bar{X}^*_s\le s\mu^*-sc_{t,s}\} \le e^{-2(sc_{t,s})^2/s}=e^{-4lnt}=t^{-4} IP{Xˉs∗​≤μ∗−ct,s​}=IP{sXˉs∗​≤sμ∗−sct,s​}≤e−2(sct,s​)2/s=e−4lnt=t−4
同理式(8)成立的概率如下：

对于条件(9)，只需要合理选择 $l$ 的取值就可以了：

上面的证明比较简单，用到了 $s_i\ge l$ 且 $n>t$ 的条件。
最后的结果就是：

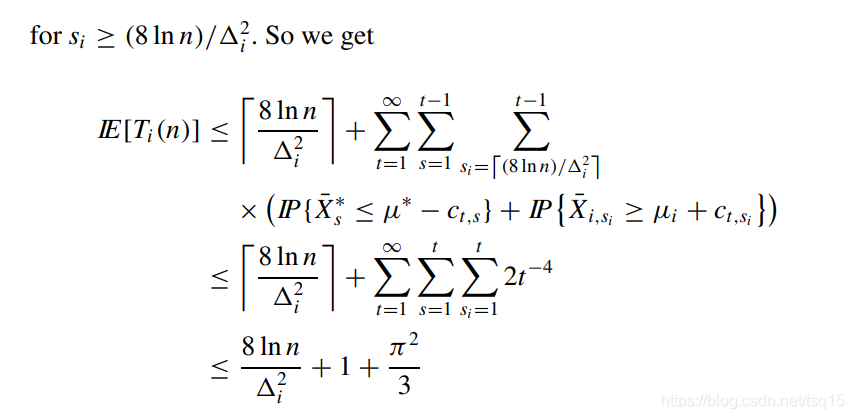
这里用到了 ${\sum }_{t=1}^{\infty }1/t^2=\pi /6$ 这个条件。

所以最后这些非最优的臂，累加起来的遗憾值也不会超过：
$$8\ast \sum _{i:{\mu }_i<{\mu }^{\ast }}(\frac{\mathrm{l}\mathrm{n}n}{{\Delta }_i})+(1+\frac{{\pi }^2}{3})(\sum _{j=1}^K{\Delta }_j)$$
也就是前面的式(2)。证毕！

小结

从证明过程可以看出，这个条件还是非常宽松的。后面不少的文章应该都给出了更优的策略。