一道弹性碰撞的物理题，结果为什么会出现π？

来源 | 《你没想到的数学》

作者 | 王赟

1

第一次波折：争议与批评

有这样一道有趣的物理题，出现在“3Blue1Brown”“李永乐老师”等许多在线视频中。

如图1.1所示，光滑的地面上放着大小两个滑块，左边是墙。大滑块的质量是小滑块的n倍。给大滑块一个向左的初速度，两个滑块之间及小滑块与墙之间会发生多次碰撞。假设碰撞没有能量损失，问一共会发生多少次碰撞？

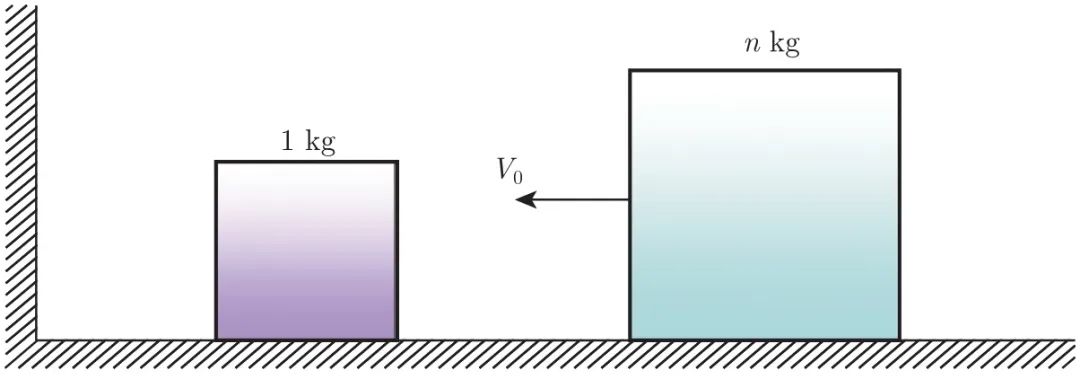
图 1.1　两个小滑块

你可能觉得，这只是一道普通的物理题而已，没什么意思。先别着急下结论，我们来看看当取一些特殊值时，分别会发生的碰撞次数。

若两个滑块质量相等，则一共会发生3次碰撞；

若大滑块的质量是小滑块的1百倍，则一共会发生31次碰撞；

若大滑块的质量是小滑块的1万倍，则一共会发生314次碰撞；

若大滑块的质量是小滑块的1百万倍，则一共会发生3 141次碰撞；

若大滑块的质量是小滑块的1亿倍，则一共会发生31 415次碰撞……

是不是觉得有意思了？当两个滑块质量之比是100的幂时，碰撞次数是去掉小数点后的前若干位。在这么一道“方方正正”的物理题里，怎么会出现与圆有关的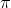呢？

“3Blue1Brown”频道给出了一个提示：凡是出人意料地出现的题目，背后总是隐藏着一个圆。而这道物理题里的圆，隐藏在能量守恒方程式中:

 常数　　　　　　　　(1.1)

其中表示大小滑块的质量，表示大小滑块的速度。我鼓励读者在继续看下去之前，先根据式(1.1)自己捣鼓捣鼓，看看能不能捣鼓出来。

2

隐藏的椭圆

式(1.1)实际上表示了空间中的一个椭圆。设大滑块的初速度为-1（负号代表向左），则能量守恒方程式可以化简为：

这个方程式表示的椭圆如图1.2所示（图中取）。在运动过程中的任何时刻，两个滑块的速度都会落在椭圆上；两个滑块的初速度，对应着短轴的下端（图中点）。

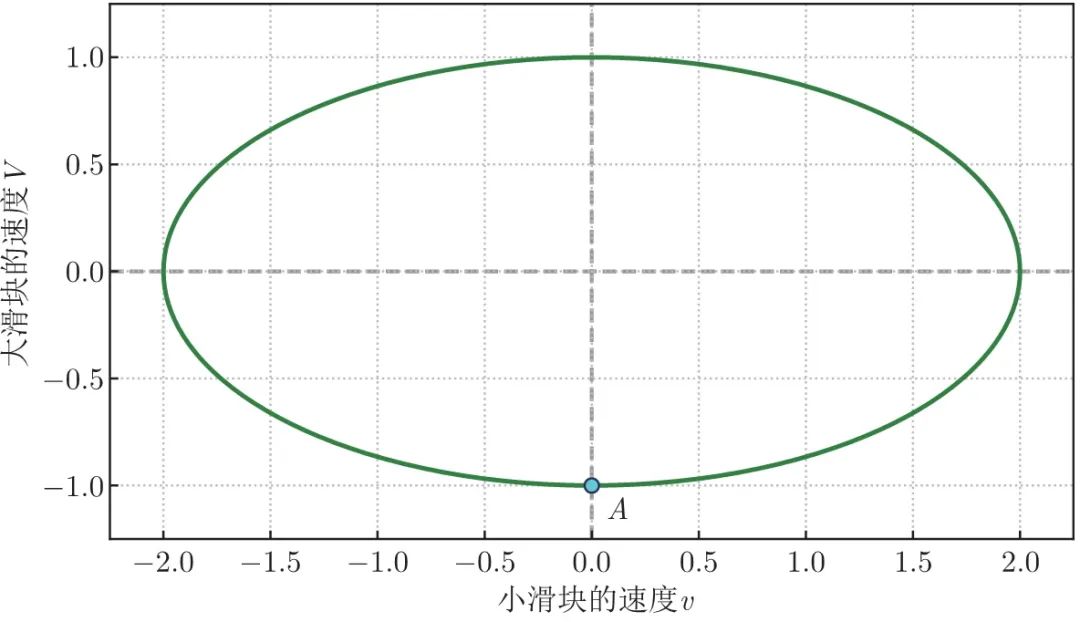
图 1.2　椭圆代表能量守恒

下面我们试着在椭圆中画出碰撞过程。第一次碰撞，是大滑块撞小滑块。碰撞前后，两个滑块的速度除了满足能量守恒以外，还要满足动量守恒，即：

 常数　　　　　　　　(1.3)

式(1.3)在空间中，代表一条斜率为的直线，这个例子中的斜率为。如图1.3，过点作一条斜率为的直线，它与椭圆的另一个交点就代表了第一次碰撞后，两个滑块的速度。

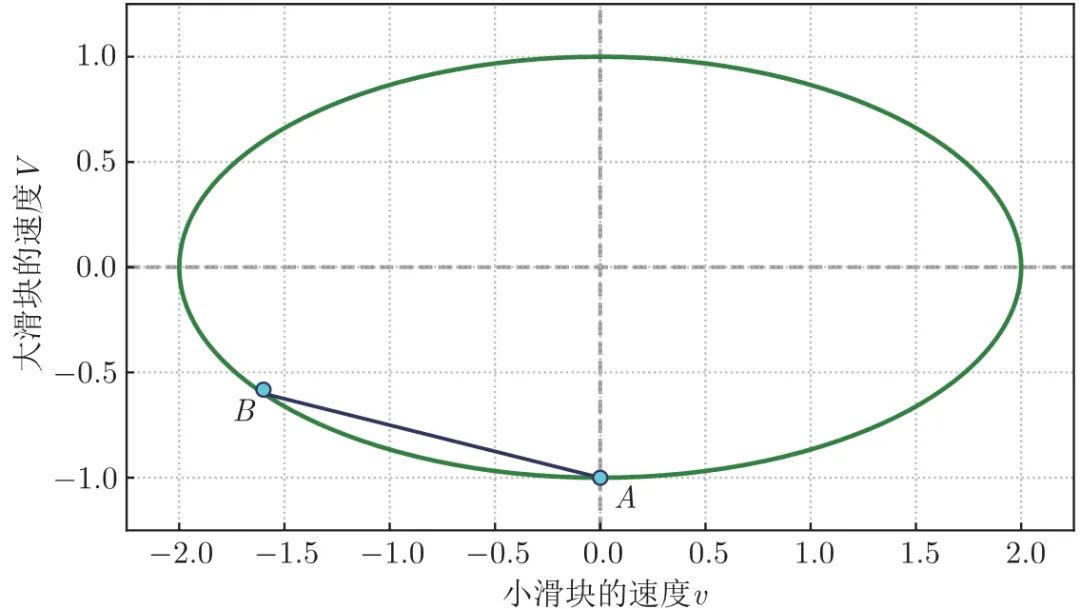
图 1.3　倾斜直线代表两个滑块相撞时动量守恒

第二次碰撞，是小滑块撞墙。其结果很简单，就是小滑块的速度变为反向。如图1.4，过点画一条与横轴平行的直线，这条直线与椭圆的交点就代表了第二次碰撞后两个滑块的速度。

图 1.4　水平直线代表小滑块与墙碰撞

重复上述过程，直到。此时，两个滑块都向右运动，但小滑块追不上大滑块了，于是不会再发生碰撞。在空间中，代表两个滑块最终速度的点一定会位于第一象限中直线上方（图中的黄色区域），这个例子中是图1.5中的点。

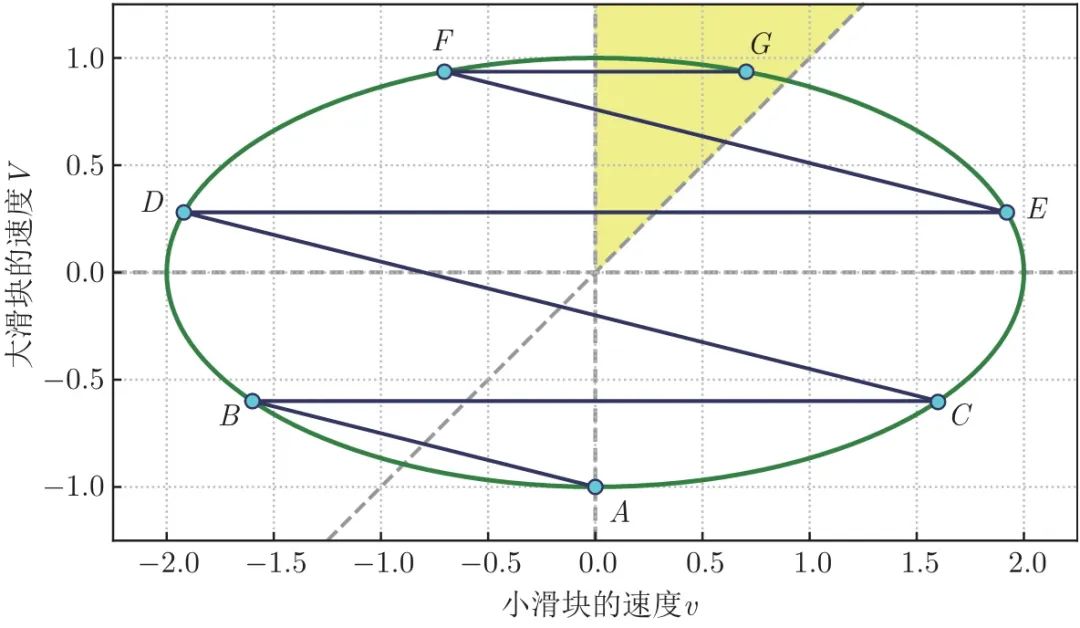
图 1.5　空间中的整个碰撞过程

3

隐藏的椭圆

可以注意到图1.5中弧、、、、所对的“椭圆周角”（角、、、、）都是相等的，等于。弧与对称，也可以让它对应“椭圆周角”，这个角也等于。联想到圆中有“等弧所对圆周角相等”的性质，而椭圆中没有，于是想到如果把椭圆“捏”成圆，会不会有意外发现？

将图1.5整体在横向上压缩到原来的倍，则椭圆就变成了单位圆，如图1.6所示。

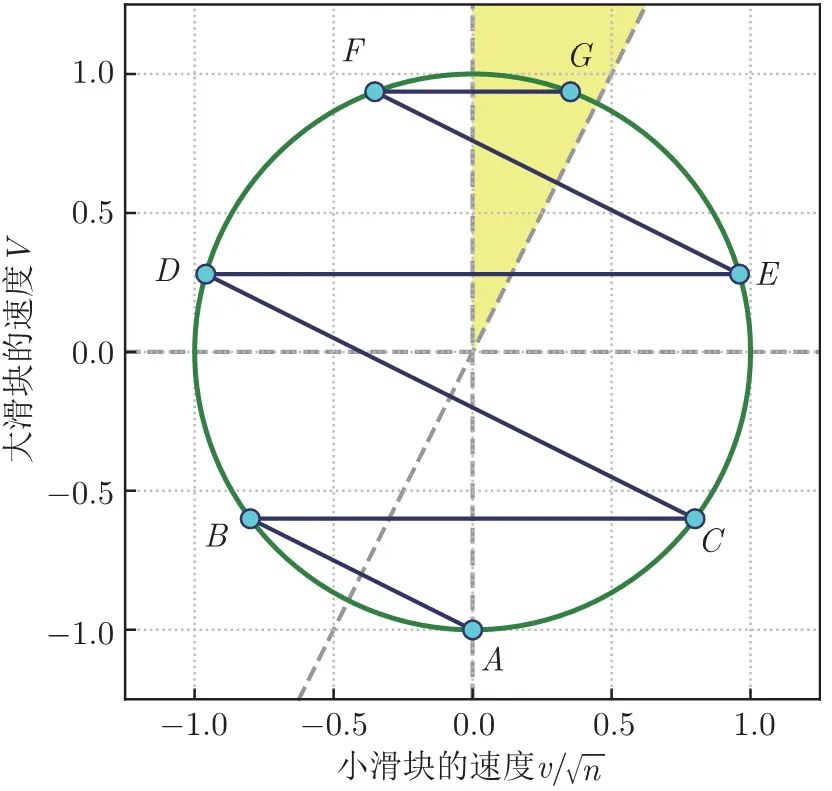
图 1.6　把椭圆“捏”成单位圆

这样一压缩，线段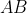、、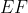的斜率就都从变成了，各段圆弧（除了）所对的圆周角也都变成了。现在可以利用“等弧所对圆周角相等”了——这些圆弧的长度，都等于这个圆周角的2倍，即。

滑块的碰撞，可以看成从单位圆上不断切下一段长度为的圆弧，直到剩余部分长度不超过为止。而整个单位圆的周长是（注意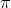出现了！），于是可以得到总的碰撞次数：

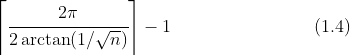
这里的取整符号看起来较复杂，实际想要达到的效果是，一般情况（不能整除时）向下取整，特殊情况（能整除时）取商再减一。请读者自行验证。

由式(1.4)可以算出，当两个滑块质量相等时，，碰撞总次数为3。而当两个滑块质量悬殊时，会很小，此时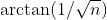可以直接用来近似表示，于是碰撞总次数约为。当两个滑块的质量之比是100的幂时，就是10的幂，这就解释了碰撞总次数为什么会恰好是去掉小数点后的前若干位。

  推荐阅读

《你没想到的数学》

作者： 王赟

有趣的数学科普书，知乎达人王赟力作，培养锻炼数学思维和计算机思维，用数学解题方法，解决生活、学习及工程问题，有思想深度的思维训练书。