对整个数学团体的不恰当描绘可能会带来不公正, 甚至可能遭到指控, 但我们还是要在此插上几笔, 探讨一下公众对数学人物的看法。
大街上普普通通的男男女女, 当他们从各方面去描绘数学家时, 可能会说数学家聪明、不实际、刻板、不善社交、全神贯注、沉默寡言、近视……或者更综合一点地形容：他们有点书生气。这是正确的评价吗?数学家是真的表现出这些个性特点, 还是某些流传的错误观念的牺牲者呢?
来源 | 《数学那些事：伟大的问题与非凡的人》
作者：[美] 威廉·邓纳姆（William Dunham）
译者：冯速
几年前, 受人尊敬的数学家, 同时也是受人爱戴的教师、斯坦福大学教授乔治 • 波利亚（George Pólya）谈及了这个问题。根据一生的经验, 波利亚总结出两个共同特征：(1)数学家都有些心不在焉, (2)数学家都行为古怪。这两点提供了很好的出发点。
心不在焉的说法似乎一语中的。很多关于数学家的民间传说都提到他们总是错过约会、投错重要论文或者丢失眼镜。例如, 有一个反复被讲的关于维托尔德 • 胡尔维茨（Witold Hurewicz）的传说, 他是一位非常有名的数学家, 一天开着车来到纽约, 停好车后去办事, 然后坐着火车回家了。第二天, 发现自家的停车位是空的, 胡尔维茨就打电话报警说发生了偷盗案。
波利亚讲述了20世纪初期新到哥廷根大学的一位年轻数学教授的故事。这位新手希望去受人尊敬的数学家希尔伯特的家中表示一下敬意。他把自己好好打扮了一番, 然后敲响了希尔伯特家的门, 应邀进来做一下简短的介绍。这位年轻人摘下帽子, 落座, 开始喋喋不休地说起话来。他很快就超过了款待他的时间。希尔伯特正全神贯注地思考一个令人费解的数学问题。就这样过了几分钟后, 希尔伯特觉得自己已经想得很明白了。于是他站起身来拿起这位年轻人的帽子, 客气地说了声再见就离开了。你也许能够猜测到这位客人的反应——他呆呆地一个人坐在这位教授的客厅里。
那些心不在焉的数学家的传说肯定不只局限于20世纪。阿基米德就是在洗澡时做出了重要的发现, 全身赤裸地跳出浴池, 兴奋无比地在大街上奔跑, 始终没有穿衣服。我们常听说艾萨克 • 牛顿在房间里工作非常投入, 以至于忘记吃给他送来的饭。有时, 当在餐厅走动时, 牛顿“漫不经心地走着, 趿拉着鞋, 袜子也没穿好, 披着一件大白袍, 头发根本没有梳理过”。
还有19世纪伟大的心不在焉的数学家之一, 德国的彼得 • 古斯塔夫 • 勒热纳 • 狄利克雷。狄利克雷在哥廷根大学数学系是高斯的继承人, 人们经常不仅把他描述成心不在焉, 而且还说他是“出了名地”心不在焉。据说狄利克雷过于全神贯注, 以至于忘记告诉他的亲家他们的第一个孙子出生了。后来孩子的爷爷知道了这个消息后, 非常生气, 于是发牢骚说狄利克雷至少应该会写“2+1=3” 吧。直到去世, 狄利克雷的心思也没有离开研究, 他的确是极度心不在焉的人。
许许多多这一类故事似乎在说, 走神是数学家们遭受的一种长期的困扰。然而, 并不是每个人都相信这一点, 所以为了公平起见, 我们简要地提一下利兹大学的约翰 • 鲍尔斯的反面观点。在一篇谈及数学家发呆的具有争议的文章中, 鲍尔斯非常直白地发表了下面的言论, 力挺这一非常聪明的群体, 他说：“认为数学家心不在焉的想法是绝对错误的。有一个权威性证明显示他们并非如此, 但是遗憾的是在这里不能提供这个证明, 因为它似乎丢失了。”
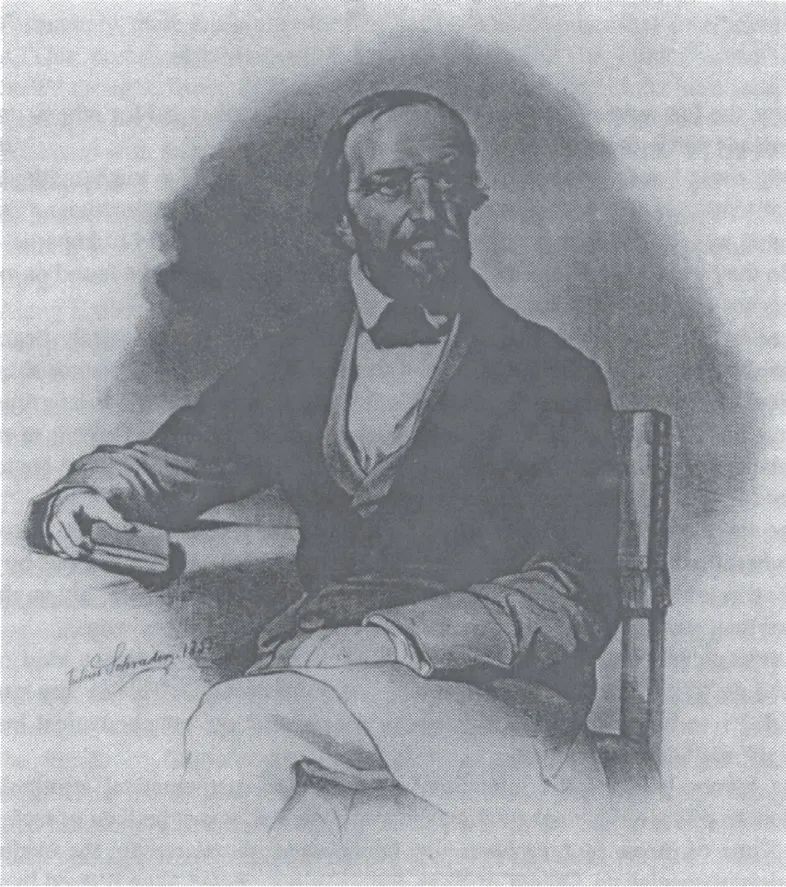
彼得 • 古斯塔夫 • 勒热纳·狄利克雷（穆伦堡学院惠允）
严肃的数学家们遭受这种“疾病”的困扰是不足为奇的。毕竟他们每天都在思索最抽象的概念、最无情的逻辑、最难以应对的挑战。普通学生觉得一小时只研究一个问题是一件耗神的事, 大多数人又如何能够想象用几个月甚至几年去攻克这样一个任务呢?这必要的精力集中是令人敬畏的, 而心不在焉也是一种必然的结果。正是心不在焉的牛顿说他仅通过“不断地思考”就做出了伟大的发现。
当一些人花几年时间不断地思考诸如质数分解或者角的三等分等问题时, 他们忽视自己的发型这类事情就不奇怪了。与数学永恒的美相比, 物质世界显得如此乏味, 如此反复无常, 如此短暂。因此, 数学家忘记取车就没有什么可惊讶的了；的确, 他们经常忘记他们自己有车。他们的身体也许是在椅子上休息, 但是他们的大脑正在穿越不同的领域。
正如上面提到的那样, 波利亚还认为数学家都是行为古怪的人。这也许是一个一目了然的情况, 因为任何人, 当他用毕生精力去考虑这些质数或三等分角问题时, 就会不由自主地表现出一定程度的古怪。当然, 表面上, 大多数数学家的行为举止很正常, 与银行家及律师没什么两样。但是在面对训练有素的观察家时, 某些迹象就会出卖他们。
一个例子就是他们的服饰。似乎很清楚, 很多数学家选择服饰时着眼于舒服而不是款式。诸如领带一类的时尚品, 对不折不扣的理性数学家来说也许是令人愤怒的。人们发现他们很少穿着丝绸服饰或者灰色法兰绒西装, 而是喜欢穿棉衬衫, 后面印有诸如
这样的题字。很多数学家对鞋的选择是凉鞋加黑短袜。还有人说, 所谓打扮就是穿上一双新运动鞋。
就此, 我们应该提一下刻画数学家的漫画, 漫画中的数学家往往穿着实验室的白大褂, 站在写满符号的黑板前。事实上, 数学家的确可能花很长时间注视着黑板上的符号, 但是他们从来不穿实验室的白大褂。这样的装扮在数学家身上是不会出现的, 就像在相扑场上看不到摔跤手的装扮一样。漫画家, 记下来吧。
毫无疑问, 男性数学家会胡子拉碴。满脸胡须是教授的非正式妆容, 也许是因为修面没有用。（如果男人需要净面, 那么为什么总是有小胡须从下巴上长出来呢?）常识表明, 大约有
的男性数学家一脸胡须。只有在几个地方, 你才可能遇到更多的大胡子, 在满是圣诞老人的圣诞集会上, 比如或者在音乐剧《屋顶上的提琴手》的谢幕舞台上。
还有就是眼镜。这非常普遍。有多少次, 当数学家发呆时, 他们把自己的眼镜放错了地方, 但总体上, 还是可以看到他们的确戴着自己的眼镜专注地看, 尽管他们凝视的对象也许是无形的方程或是看不见的多边形。
人们还知道数学家都有与众不同的幽默感——常常被说成“干燥”的那种幽默, 也许被说成“烤干”的幽默更精确。接下来再把这种幽默分成两个范畴, 分别把它们称为“低级”数学幽默和“高级”数学幽默。
低级幽默指的是有意使数学术语发生混淆。在过去的十几个世纪, 数学家们已经发明很多专业术语。其中一些术语, 如同伦或者微分同胚等只限于少数专家“享用”。而另一些, 如矩阵、参数等已经成为普通语言, 在日常事务中它们经常被用错。然而, 还有一些情况, 日常生活中的词汇被借用或引用到数学家的词典中来。但它们有非常精确的数学意义, 例如域、群和束等。
这一切使得数学家能够高兴地把这些词汇的专业含义与它们的通常意义交换。他们把同行的集合称为“有限群”, 并发出会心的笑声。他们把双胞胎的集合描述为“不相等但同构”。当情况取得进展时, 数学家就说它有一个“正导数”。
数学家还利用近音词开玩笑。有人也许听说过这样的笑话, 把单词“斜边”用一种大型哺乳动物的名字来代替 。常数
也许是取笑烤制甜点（pie）的最常用的恶搞双关语（参见第C章中的漫画）。在第G章对《几何原本》的讨论中, 我们极力克制着才没有使用那个被滥用但又非常优美的副标题“这里在观察正常锁骨” 。
幸好, 还有远比这些低级的双关语更高级的数学幽默。它们通常涉及一些曲解逻辑的事情。稍稍思考一下, 就可以由某些逻辑矛盾产生这样的幽默。作为逻辑驾驭者的数学家们发现, 当逻辑这辆车掉轮子时会很有趣。
我们先举一个波利亚的例子。晚年回首一生, 波利亚回顾了他对哲学这门学科的长期影响, 并写道：“谁是哲学家?答案是：哲学家是这样的一个人, 他知道所有事却不知道其他任何事。”这一妙语是数学家们觉得很有趣的一种逻辑变通。
物理学家沃尔夫冈 • 泡利（Wolfgang Pauli）说了一句类似的话。泡利才华超人, 但也非常傲慢, 一次在讽刺一位新同僚时, 他说了一句非常滑稽的话：“他还这么年轻, 就早已默默无闻了。”此外, 斯蒂芬 • 博克（Stephen Bock）曾描述一个隐士和他的梦想：“杰从书中只知道阅读这件事, 但自己一点都不想去读书。”
这种逻辑的使用或误用在数学家亨利 • 曼恩（Henry Mann）的故事中也体现得很充分。据说亨利 • 曼恩开车带几个同事到辛辛那提参加学术会议, 由于不熟悉辛辛那提的街道, 曼恩迷路了。他的同事们尽管很不安, 但仍然保持安静, 最后他们终于意识到他已经逆行进入单行道。但是曼恩不理睬他们的警告。他说这条街不可能是单行道, 因为他们的车一直沿着一个方向前进, 而且其他很多交通工具都从另一个方向向他们驶来。
这些都是完全颠覆了逻辑的例子。下面这个故事的幽默在于英语发音的不合逻辑。波兰数学家马克 • 卡克（Mark Kac）移民来到美国, 并设法掌握有时候令人费解的英语。令他着急的是那些结尾拼写相同却有不同发音的单词。例如, 单词结尾的“ow”有时候发长音
, 如在grow 或know中, 有时候却不是, 如在cow 或how 中。单词bow 有两个不同的发音, 这更加糟糕。
一直与这一现象搏斗的卡茨教授突然意识到snowplow 更加稀奇古怪, 因为“ow”在同一个单词中却有两个不同的发音。注意到这些之后, 他格外小心地去记住它不合逻辑的发音。遗憾的是, 他把这两部分的发音弄混了, 本来与grow-cow有相同韵律的snowplow被他按cow-grow的韵律念了出来。
最后, 讲一个别有风趣的故事。在一次数学会议的会下, 一位年轻的崇拜者向著名数学家宾（R. H. Bing）要签名。拿着宾的签名, 她让另一位著名数学家保罗 • 哈尔莫斯（Paul Halmos）在同一张纸上签名。然后她手里拿着这张如同数学论文的东西让如下数学家一一签了他们各自的大名：吉尔伯特（Gilbert）和苏利文（Sullivan）, 吕特（Ruth）和格里克（Gehrig）, 西斯科尔（Siskel）和艾伯特（Ebert）。
当她把这份奖品给她的一位同事看时, 这位同事立即说：“我出25美元, 你把它给我吧。”此时, 另一位更聪明的数学家突然冒出一句：“很好, 但如果你让我在这些人的名字下面签上我的名字, 我出50美元。”
以上这些例子展示了数学家之间崇尚的一种幽默。人们可能要略加思索才能领悟, 而大家普遍的反应不一定是因此发笑, 而是很欣赏它。数学幽默既不是下流话也不是闹剧, 而往往是非常理智的。有人猜测系列喜剧《活宝三人组》的粉丝俱乐部应该几乎没有数学家。
如果服装和幽默、古怪和心不在焉让数学家显得格格不入, 那么他们的这种共同特性也可以被看成某种防御机制。他们确实是在数字中寻找力量。
例如, 人们普遍有这样的印象, 数学家只不过是会计师, 他们日复一日地把一列数加起来。数学家和诗人乔安妮 • 格罗尼（JoAnne Growney）面对这样的看法, 利用下面的诗句淋漓尽致地描绘了这样的场景：
误解
啊, 你是一位数学家,
他们带着羡慕或者轻蔑说着。
然后, 他们说,
我可以雇用你为我记账。
我想了一下账目,
偶尔,
我自己记账,
就像偶尔清扫高高的架子上的灰尘一样。
人们误解了数学家吗?肯定是。他们被轻视了吗?毫无疑问。当某人被介绍说是一位数学家时, 时常会听到下面这两条评语之一：“我讨厌数学”或者“我害怕数学”, 当然也可能是这两条结合到一起“我既讨厌又害怕数学”。
为什么数学家总是遭到这样的评论轰击呢?为什么很多人把这门学科看得如同没有麻醉的眼科手术一样吓人呢?他们是不是在童年受到数学家的刺激了?调查之后, 你会发现数学恐惧症有两个共同源头：要么是这么说的人曾有一位可怕的数学老师, 要么是这人已经认识到自己的确缺少数学才能。
拿没有遇到好老师当作借口的情况相当普遍, 而且相当值得关注。忘记诸如自己的结婚纪念日或者总统名字的人却能够非常清楚地记得十几年前讨厌的代数老师。琼斯先生或者史密斯女士是否真的如说的那样可怕, 或者这些不好的记忆是否有更深层、更黑暗的起因, 这些需要我们反省。
然而, 虽然成千上万的人以糟糕的数学老师为借口, 但更普遍的解释则是：“我从来学不好数学, 也永远不想学数学。”这是每一位数学老师听到过上百次的自白。它暗示数学学得好坏完全取决于遗传。正如某些人一出生就有蓝眼睛一样, 一些人一出生就有学数学的才能。如果你不是天生如此, 那么你注定是一个数学不行的人, 没有什么能够改变这种命运。
人们的这种观念不太容易消除。在数学上遇到困难的人经常马上下结论说, 这种失败是他们的命运所致, 而不是因为他们自己。很少有人会反驳说：只要稍微用功一点儿就能学好。
数学家遭到这种猛烈的攻击也只能保持低调。其他学科的同仁很少遇到这样的状况。很难想象在历史课上会有下面这样的交锋：
教授：“乔治, 内战时期的美国总统是谁?”
乔治：“嗯——嗯——嗯——很抱歉, 教授, 我从来学不好历史。”
遗憾的是, 有些人一边喊着恐惧数学一边又很珍爱它。即便是对受过高等教育的人来说也是如此。如果一位数学家吹嘘说他从来没有读过一句诗, 那么他会被人们贴上无知蠢人的标签。然而, 承认自己是数学盲的诗人却经常因顶着这顶无知帽子而感到很自豪。真是不公平。
缺乏对数学的理解就不能领会数学思想的真正意义。想象下面这样的场面：
我们在一次鸡尾酒会上看到很多有学识的男男女女, 自我吹嘘地聊着天。一名生物学家站到钢琴的前面, 正向一名全神贯注的听众讲解科莫多巨蜥的进食习性, 而此时沙发旁边一些人正在热烈讨论着加利福尼亚州葡萄酒的酒香。这些话题不仅对专业人士来说可以理解, 对一般的听众来说也能理解, 甚至对那些并非动物学家或厨师的人来说也能理解。
交谈突然停了。在一个角落里, 一名数学家喝了一口无酒精姜汁饮料, 笨拙地抚弄着一个塑料铅笔筒, 嘴里念叨着：
交谈停止。玻璃杯的碰撞声消失了。出现了死一般的沉静。人们看表的看表, 找外套的找外套。很多人露出恐惧的表情。酒会结束了。
事实上, 上面的公式
不仅是正确的, 而且是我们理解正态概率分布的关键。而正态概率分布则是统计推断的核心。医学研究、投票数据以及其他很多重要问题都依赖于这个公式的正确性。因此, 它比科莫多巨蜥和佐餐葡萄酒对现代生活的意义更重大。然而, 几乎没有非数学人士对这一串符号所蕴含的威力表现出哪怕是些许的感激之情。只有那些数学家才真正“了解”。作为一个团体, 他们必须尽最大可能去应对公众对他们的不理解。生活真是很辛苦。
因此, 如果你遇到一群人, 他们戴着眼镜, 有些发呆, 所有人都认真地谈论着, 其中一些人穿着短袜和凉鞋, 却没有人穿着实验室的白大褂；如果他们是几个人围着一张三角形桌子在说一些没有意思的俏皮话；或者, 如果他们都不觉得《活宝三人组》有意思, 那么你可以打赌, 你面前的这些人是研究数学的。请对他们友善些。
无需动用纸笔，纵览数学世界不可不谈的伟大定理、难题和争论；好奇心大满足，纵览数学的核心知识和历史八卦。
本书是一部短文集，文章以各自英文标题的首字母按照A到Z的顺序排列，每一篇短文都讲述了一个特定的数学主题，介绍了数学世界不可不谈的伟大定理、难题、争论和不解之谜。
推荐阅读
《数学那些事：伟大的问题与非凡的人》
作者：威廉·邓纳姆
译者：冯速
无需动用纸笔，纵览数学世界不可不谈的伟大定理、难题和争论；好奇心大满足，纵览数学的核心知识和历史八卦。
本书是一部短文集，文章以各自英文标题的首字母按照A到Z的顺序排列，每一篇短文都讲述了一个特定的数学主题，介绍了数学世界不可不谈的伟大定理、难题、争论和不解之谜。
01
《改变世界的17个方程》
作者：[英] 伊恩•斯图尔特
译者：劳佳
•英国数学科普名家伊恩•斯图尔特经典名作，译为多国语言
•李永乐推荐科普名作，“欧拉图书奖”获奖作品
•美国数学学会（AMS）&美国数学协会（MMA）联袂推荐
了解世界运转的深层道理，看懂科学发展的规律
方程是一首首数学的诗，言简意赅，却充满意义。阐释自然与社会现象，连接数学与物理现实，是方程的力量与美之所在。
02
《微积分的历程：从牛顿到勒贝格》
作者：邓纳姆
译者：李伯民 汪军 张怀勇
本书荣获“第七届文津图书奖推荐书目”。
这不是一本数学家的传记，而是一座展示微积分宏伟画卷的陈列室。书中的每一个结果，从牛顿的正弦函数的推导，到伽玛函数的表示，再到贝尔的分类定理，无一不处于各个时代的研究前沿，至今还闪烁着耀眼夺目的光芒。
03
《世界是概率的：伊藤清的数学思想与方法》
作者：[日]伊藤清
译者：刘婷婷
伊藤清是如何学习和思考数学的？
数学家如何看待“纯粹数学与应用数学”“直观与逻辑”？
现代概率论是如何一步步发展起来的？
沃尔夫奖、高斯奖得主，现代随机分析之父日本数学大家伊藤清
讲述数学思想与方法 激发关于概率与世界的深层呈现日本数学发展的另类线索
04
《数学与创造：广中平祐自传》
作者：广中平祐
译者：逸宁
菲尔兹奖、日本学士院奖、日本文化勋章得主日本数学大家广中平祐亲笔自传
作者以解决“奇点解消问题”的故事为线索，讲述了自己如何学习数学、走上数学研究道路的历程，分享了在挑战数学难题过程中的思考方法与感悟，并就“数学与创造”“创造与情绪”“分析与大局观”等话题做了深入阐述。
05
《春夜十话：数学与情绪》
作者：冈洁
译者：林明月
天才数学家的极意文集、影响几代人的不朽名作。
本书从“情绪与心智”的角度，论述了认知发展、义务教育中的深层问题，同时阐述了对人性的细微考察与独到理解，是一本影响了日本几代人的经典名作。
06
《一个定理的诞生：我与菲尔茨奖的一千个日夜》
作者：塞德里克•维拉尼
译者：马跃 杨苑艺
畅销世界的当代数学家传记，知名数学家塞德里克·维拉尼荣膺菲尔茨奖的精彩历程，真切感受数学研究生涯的艰辛与乐趣，了解数学家的日常工作与思维方式。
07
《牛顿传：科学天才的浮生一梦》
作者：詹姆斯•格雷克
译者：欧瑜
文津奖获得者、科普作家、百万级畅销书作者詹姆斯·格雷克所著传记，故事、历史与科学的结合，展现牛顿辉煌的科学成就，剖析其鲜为人知的内心世界。
在这本传记中，格雷克借助牛顿的重要信件和未出版的笔记，记述了这位科学界最伟大人物之一的生活经历、与他有关联的人物，以及对他产生影响的重要事件，并勾勒出他所处的历史时期的全貌。
08
《我只会算术：小平邦彦自传》
作者：[日]小平邦彦
译者：尤斌斌
小平邦彦“抄书学数学”的传闻是真的吗？宽松的教育，是否会影响思考能力，又该如何改善？日本的现代数学研究是如何传承和发展的？
菲尔兹奖、沃尔夫奖、日本文化勋章得主日本数学大家——小平邦彦， 亲笔自传
澄清“抄书学数学”之传言，评判日本“宽松教育”的利弊得失
还原“懒惰凡人”到“菲尔兹奖得主”的真实样貌
讲述小平邦彦的数学学习心得与感悟，展现日本数学与科学发展的隐性脉络
09
《一个数学家的辩白（双语版）》
作者：戈弗雷·哈罗德·哈代
译者：何生
英国数学家戈弗雷·哈罗德·哈代的经典名篇，被称为是“用优雅的语言对数学真谛进行了完美的揭示”。
本书是哈代于1940年写成的心得之作，展现了数学之美、数学的持久性和数学的重要性三大主题。
10
《一个应用数学家的辩白》
作者：[美]劳埃德•尼克•特雷费森（Lloyd Nick Trefethen）
译者：何生
1940年，哈代出版了《一个数学家的辩白》，这是一位领先的纯数学家对数学的沉思。82年后，《一个应用数学家的辩白》是一位具有哲学倾向的数值分析师的沉思，也是他的个人回忆录。作者在数值分析的工作中找到了极大的乐趣，但对它与其他数学领域的关系感到困惑。本书更准确的书名应该是《一个数值分析师的自白》，它包含更多的传记材料和更多的数学内容，尤其是在后半部分。但两本书的目的是相同的，都是从作者自己的角度对数学进行严肃的沉思。
扫一扫
9
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
