豆瓣9.3，这本书真正做到了国内泛函分析教材入门的天花板！

应用数学领域先驱欧文·克雷斯齐格的《泛函分析导论及应用》被欧美众多大学广泛用作数学系、物理系本科生和研究生的教材．这本书作为该领域最好的入门书，受到广大读者的认可。

“我想不出比它更好的泛函分析学习材料了，这本书非常适合学过实分析、线性代数的本科生和低年级研究生阅读。” 

“重基础，几乎没有啰唆的地方，一气呵成。看这本书能把泛函的精髓把握住，完整却不拖泥带水，把框架理顺了，遇到实际问题就可以知道要去哪里找答案。 ”

“读起来很轻松，完全不用在大脑内载入过多无用信息。简洁、门槛低、有答案、可自学，推荐给广大工科学生。”

《泛函分析导论及应用》

作者：[加]欧文•克雷斯齐格（Erwin Kreyszig）

译者：蒋正新 吕善伟 张式淇

来源：知乎 dhchen

经过现代数学训练的人看待函数是通过“映射”来看的，但是在20世纪初，希尔伯特的那个年代，大家还是默认函数=公式，也就考虑函数的时候更多的是去想那个函数的具体取值而不是现在的把函数看成一个集合映射到另外一个集合的映射，也就说有一个显示的公式表达是很重要的。而考虑“函数的函数”的时候，这种表达就变得模糊了。这也是Hilbert和Fredholm在考虑积分方程这个问题时异常困难的点。上一篇文章大家估计看得云里雾里，因为那个时候泛函分析也是在云里雾里，这篇文章主要是介绍泛函分析的“起源”，泛函分析的“定义”。

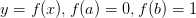, 我们计算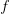绕着x轴围成的物体的表面积，它的表达式为。

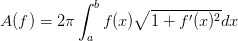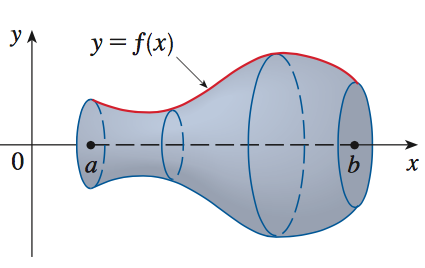我们想要找到使得这个曲面最小的那个函数。这是一个典型的“函数的函数”，输入一个函数，得到一个值。学过一点微积分的知道，一般的函数求最小值的方法是求导，找出让导数等于0的点。如果按照这个思路，我们必须去定义这种 “函数的函数”的微分。

其实找到一个“函数的函数”的最值问题就是“变分法”的核心问题。另一个比较出名的问题是等周问题：周长固定的情况下什么曲线围成的面积最大。Volterra称呼这类函数是“曲线的函数”，它们的变量是曲线。Hadamard给了一个不同的名字：fonctionelle。后面这个名字变成了functional (泛函)，而它把这个分析泛函的学科(变分法)叫做“泛函分析”。Hadamard的影响是巨大的，有一个学生叫Frechet

没错，就是这个人，这个人给出泛函（函数的函数）的求导方法。

同时，两个意大利人：G. Ascoli 和C. Arzela 考虑了如下一个问题：对于一列连续函数列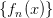, 下面积分和极限可交换的一个充分条件是：一致收敛。

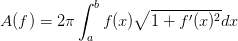所以，他们就考虑什么时候一列连续函数列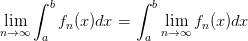是一致收敛的（或者说，至少存在一个子列是一致连续的）。之所以提这个是因为他们第一次把集合论引入了函数研究，他们研究了“函数的集合”，之前虽然康托尔已经开始研究集合了，他关注的是数的集合。

Frechet的抽象公理化：

无可置疑的是在分析的公理化这件事情上Frechet的贡献是最大的，他关注一个问题：如果不使用坐标去定义微分。之前定义微分是需要坐标这个概念的，这一点限制了对泛函求导，因为它们没有坐标（或者说它们是无限维的）。

这里我们论述一下希尔伯特处理无限维空间的思路，具体的会在下面展开。希尔伯特用一串无限的数列（广义的傅立叶系数）来替换函数，然后他去处理那些数列而不是函数本身。这本质上是“坐标”这一概念的遗留。下面是他在1928年的原话：

We believe that this method has played an important role in seconding intuition, but that its time has ended. It is a useless artifice to substitute for a function an infinite sequence of numbers which, moreover, may be chosen in a variety of fashions. This is quite evident, for example, in the theory of integral equations where the solutions of Fredholm and Schmidt are much simpler and more elegant than those of Hilbert, which is not to take away from the latter the essential merit of having obtained a great number of new results

他提倡一种“广义分析”或者说“泛函分析”，他认为这种分析要基于两个要素：

1. 集合论

2. 集合（空间）中极限（本质上就是今天的拓扑）

他提倡的东西用现代的语言来看就是点集拓扑。他定义了度量空间：也就是一个函数的集合，其中任何两个函数之间都可以定义“距离”（比现在的度量狭隘一点）。 最关键的他意识到，光有集合是不够的，我们需要附加一个结构，使得这个集合中元素之间可以相互比较差异。这个想法是革命性的，因此他也不断的推销这个想法，即使到了1950年。

比较倒霉的是虽然这位老哥的想法长留于世，但是他作出的结果在今天看来都太简单了。所以泛函分析的书上很少有定理是用他的名字命名的，留下来的是用他的名字命名的概念。不过，他写出了第一本泛函分析的教程，这个教程影响了一大批人，包括Hausdorff。

01

《泛函分析导论及应用》

作者：[加]欧文•克雷斯齐格

译者：蒋正新 吕善伟 张式淇

泛函分析学习的优秀入门书，被欧美众多大学广泛用作数学系、物理系本科生和研究生的教材，深入浅出、清晰易懂，富有知识性和趣味性，可用于自学。

简洁、门槛低、有答案、可自学，推荐给广大工科学生。