
数学界一般都很平静,但不鸣则以一鸣惊人:年仅34岁的纽约大学柯朗数学研究所副教授王虹(Hong Wang)与不列颠哥伦比亚大学的约书亚·扎尔(Joshua Zahl)合作,在预印本网站arXiv上提交了一篇长达127页的论文,宣告攻克了困扰数学界一个多世纪的三维挂谷猜想(Kakeya Conjecture)。
菲尔兹奖得主、著名数学家陶哲轩(Terence Tao)也在第一时间于其博客撰文推介,盛赞此项工作“展现了非凡的创造力”。
如果成果得到验证和认可,王虹或许将成为继玛丽安·米尔扎哈尼(Maryam Mirzakhani)和玛丽娜·维亚佐夫斯卡(Maryna Viazovska)之后,第三位摘得菲尔兹奖桂冠的女性。

王虹,2007年进入北京大学地球与空间科学学院学习,后转系至数学科学学院,跟随王立中老师做本科生科研,并在刘张炬老师指导下完成毕业论文《经典Hodge理论和度量空间上的Hodge理论》,2011年获北京大学数学学士学位;2014年获巴黎综合理工学院工程师学位和巴黎第十一大学硕士学位,2019年获麻省理工学院博士学位。
她于2021年6月完成在普林斯顿高等研究院的博士后研究工作,并于当年7月起任加州大学洛杉矶分校(UCLA)助理教授,2023年7月起任纽约大学库朗数学研究所副教授。
王虹主要致力于傅里叶分析研究。2022年9月,她与其他两位年轻学者共同获得Maryam Mirzakhani New Frontiers Prize,该奖项由突破奖基金会于2019年设立,以纪念2017年不幸去世的首位女性菲尔兹奖获得者——Maryam Mirzakhani。
获奖人须为在过去两年之内(从奖项启动评选算起)获得博士学位的女性数学家。王虹因其在限制性猜想、局部光滑性猜想及相关问题上的研究进展而获奖。
01
挂谷猜想:数学领域的经典难题
1917年,日本数学家挂谷宗一(かけやそういちSoichi Kakeya)提出了数学界著名的挂谷问题,其数学表述为:长度为1的线段在平面上做刚体移动,方式不限,转动也罢,平移也行,总之不惜采用任何手段,只求转过180度调头,试问:扫过的最小面积是多少?
他在提出此问题的同时,也给出了自己的猜测,也即至今未解的Kakeya猜想:最小单连通域的面积可能趋于零!
挂谷先生为何会提出这么一个烧脑的问题呢?原来他的祖国日本,人多地少,资源捉襟见肘,尤其体现在二战时闪转腾挪很憋屈,也难怪那时候提出了大东亚共荣圈的构想,不过在亚洲邻国眼里,这个共荣圈的本质就是侵略,远比不上中国如今的一带一路。
言归正传看一看问题的原型:一位武士在上厕所时遭到敌人袭击,矢石如雨,而他只有一根短棒,为了挡住射击,需要将短棒旋转一周360°(支点可以变化)。但厕所很小,应当使短棒扫过的面积尽可能小。面积可以小到多少?
如梭光阴已是2017年,算是该猜想等待证实或证伪的100周年大“庆”,尽管尚无成果可庆。
简略回顾求解历程:
正如1+1=2的哥德巴赫猜想一样,看似简单的数学证明,一定能吸引从文盲到大数学家的蜂拥而至。哎,想当年我也蠢蠢欲试。
为方便比较,所有给出值都规整为转过360度,除以2便可得扫过180度时的值。
先看没有技术含量的“文盲解”和“小学生的解”,前者以线段的任一端作为圆心旋转,后者以线段中心为圆点旋转,后者以节省75%的回旋面积完胜前者,简单得再添一句描述都显得多余。如下图所示:

数学家们肯定不会考虑上述这些几乎没有技术含量的东西。在挂谷宗一提出这个问题后,有数学家发现,若这个线段在正三角形(高为1,边长为2/√3)中每一顶点处都旋转60°,可以算出这种情况下,线段扫过面积为1/√3= 0.58,比小学生的解0.78略有进步。如下图:
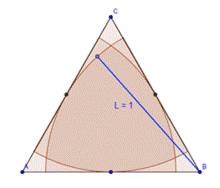
当然,若线段夹在两个圆之间,转过180°的面积既小于整个圆环,又大于半个圆环,当内圆的半径无限增大时,面积趋近于π/8,但始终不等于π/8= 0.39,比前者0.78又厉害了一倍多。如下图:
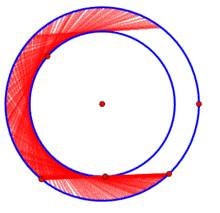
能否让扫过的面积刚好为π/8呢,挂谷宗一本人想到的是借助三尖内摆线,计算表明,这种情况下线段扫过的面积是π/8。挂谷本人及其他许多数学家都认为这就是最小面积了。
1928年,前苏联数学家贝西科维奇(Besicovitch,AbramSamoilovitch,1891-1970)差那么一点就解决了这个问题,答案是可以任意小。
精确描述并理解他的求解过程,得具有数学家的大脑,这显然也超出了本文的科普定位。有兴趣的朋友只好自行探究了。这里仅给出其中涉及到的佩龙树,如下图:
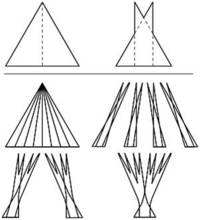
显然上述解答几乎50%地证明了挂谷猜想,唯一没能实现的是单连通域!也就是说调头过程中,线条难免有时要举高无限小高度再转一下,从一个连通域切换到另一个连通域。显然其意义大打折扣。
1971年坎宁安F.Cunningham终于在单位圆内作出面积可以非常小的单连通挂谷集,解决了单连通性和有界性两方面的问题。同时,他证明了如果限于星形(即图形内存在一点,连接它与图形中任一点的线段整个在图形中),则挂谷集的面积不小于π/108 = 0.029。
然而无限趋于零的单连通回旋面积仍然遥遥无期。
02
王虹和 Joshua Zahl 的证明思路与突破
王虹和 Joshua Zahl 此次的证明,采用了独特的方法,巧妙地将问题与其他数学概念和理论建立联系。他们从全新的视角切入,把三维挂谷猜想中的几何问题转化为代数和分析问题,通过一系列复杂的推导和论证,给出了他们认为合理的证明过程。
从已公开的信息来看,他们的证明关键在于构造了一种特殊的数学结构,利用这种结构来刻画挂谷集的性质,成功绕过了以往研究中遇到的诸多障碍,为解决三维挂谷猜想开辟了新的道路。这一突破,就像是在黑暗中找到了一丝曙光,让人们看到了最终解决这个猜想的希望。
03
对数学研究的深远意义
如果这一证明最终被证实是正确的,那它对数学研究的意义将不可估量。一方面,它将彻底解决三维挂谷猜想这一长期悬而未决的问题,为数学的发展填补重要的空白;另一方面,证明过程中所使用的方法和技巧,可能会为其他数学领域的研究提供新的思路和工具,推动整个数学学科的发展。比如,在调和分析中,挂谷猜想的解决可能会帮助数学家们更好地理解函数的性质和变换;在数论中,也可能为某些数论问题的研究提供新的视角和方法。
从1917年的旋转针问题,到2025年的三维突破,Kakeya猜想走过了一个多世纪的探索之路。王虹和 Joshua Zahl 在 arXiv 发布的对三维挂谷猜想的证明,是数学领域的一次重要尝试。
无论最终结果如何,它都已经引发了广泛的讨论和思考,为数学研究注入了新的活力。我们期待着学界对这一证明的进一步验证和解读,也期待着数学领域能因这一成果取得更多的突破和进展。
图灵出版的菲尔茨奖得主著作

《可变思考:数学与创造性思维》
作者:[日]广中平祐
译者:佟凡
日本数学大家、菲尔兹奖得主广中平祐著作!稻盛和夫力荐,呈现数学家观察事物的独特视角与思考方式。
1.稻盛和夫力荐,日本累计销售10万册!
2.菲尔兹奖得主理解“复杂”与“变化”的巧妙视角,用数学的智慧探索创造力的本质
3.讲述创造性思维的本质与根源传授学习、研究、教育中的创造性思维的模式与方法
01

《数学与创造:广中平祐自传》
作者:广中平祐
译者:逸宁
菲尔兹奖、日本学士院奖、日本文化勋章得主日本数学大家广中平祐亲笔自传
作者以解决“奇点解消问题”的故事为线索,讲述了自己如何学习数学、走上数学研究道路的历程,分享了在挑战数学难题过程中的思考方法与感悟,并就“数学与创造”“创造与情绪”“分析与大局观”等话题做了深入阐述。
02

《陶哲轩教你学数学》
作者:陶哲轩
译者:李馨
菲尔兹奖得主陶哲轩数学思维大解析,通过奥数竞赛习题解答,带你领悟数学之美。
本书是国际知名数学家陶哲轩15岁时的著作,从青少年的角度分析数学问题,主要是数学竞赛等智力谜题,用学生的语言解释思考过程,完整展现了少年陶哲轩的解题思路。
03

《一个定理的诞生:我与菲尔茨奖的一千个日夜》
作者:塞德里克•维拉尼
译者:马跃 杨苑艺
畅销世界的法国当代数学家传记,知名数学家塞德里克·维拉尼荣膺菲尔茨奖的精彩历程,真切感受数学研究生涯的艰辛与乐趣,了解数学家的日常工作与思维方式。
04

《惰者集:数感与数学》
作者:[日]小平邦彦
译者:尤斌斌
一览数学世界不可不谈的伟大定理、难题和争论
勾勒数学的全景,让课堂上的知识变得更清晰、更好懂
数学科普巨匠邓纳姆献给钟情数学以及单纯好奇“数学到底是什么”的读者
05

《我只会算术:小平邦彦自传》
作者:[日]小平邦彦
译者:尤斌斌
小平邦彦“抄书学数学”的传闻是真的吗?宽松的教育,是否会影响思考能力,又该如何改善?日本的现代数学研究是如何传承和发展的?
菲尔兹奖、沃尔夫奖、日本文化勋章得主日本数学大家——小平邦彦, 亲笔自传
澄清“抄书学数学”之传言,评判日本“宽松教育”的利弊得失
还原“懒惰凡人”到“菲尔兹奖得主”的真实样貌
讲述小平邦彦的数学学习心得与感悟,展现日本数学与科学发展的隐性脉络
06

《几何世界的邀请》
作者:[日]小平邦彦
译者:李慧慧
平面几何是观察判断与逻辑思考的精妙结合,是初等数学教育中培育创造力的好途径。本书为日本数学家、菲尔兹奖得主小平邦彦先生的几何入门作品,书中以欧几里得几何、希尔伯特几何、复数与几何为轴线,由浅入深,层层深入,从作为图形科学的几何、作为数学的几何等不同角度介绍完整的几何世界,是几何入门、训练思维与创造力的佳作。
07

《陶哲轩实分析(第3版)》
作者:[澳]陶哲轩(Terence Tao)
译者:李馨
本书源自华裔天才数学家、菲尔兹奖得主陶哲轩在加州大学洛杉矶分校教授实分析课程的讲义。
全书从分析的源头——数系的结构和集合论开始,然后引向分析基础,再进入幂级数、多元微分学和傅里叶分析,最后介绍勒贝格积分,几乎完全是以具体的实直线和欧几里得空间为背景,完美结合了严格性和直观性。
























 83
83

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








