
数论是纯粹数学的分支之一,主要研究整数的性质。而整数的基本元素是素数(也称质数),所以数论的本质是对素数性质的研究。数论被高斯誉为“数学中的皇冠”。
哥德巴赫猜想、孪生素数猜想、斐波那契数列、黎曼猜想,无比引领着数学大师们前仆后继的去探索。
本文选取
《证明的故事:从勾股定理到现代数学》
作者:[澳] 约翰·史迪威(John Stillwell)
译者:程晓亮 张浩
自然数 0, 1, 2, 3, 4, …是最基本的数学对象,在某种程度上每个人都能理解。它们也是数学中最古老的未解之谜的主题。例如,是否存在奇完全数?是否存在无穷多对孪生素数?然而,直到最近,数论还经常被揶揄为“各种伎俩”,对大多数数学家来说,数论没有什么用处,也无法引起他们的兴趣。
近几十年来,当世界变得数字化,数字成为其命脉,需要加密的保护,而这最终依赖于数论时,人们的态度发生了改变。所以当今的问题不是为数论辩解,而是理解它。
正如我们将在本章看到的,数论很难,因为它的证明方法几乎涉及数学的所有领域,包括几何、代数、微积分,还有一些我们还没有讨论过的领域,比如拓扑学。这是令人惊讶的,因为数论有极其简单的要素:0、把一个自然数带到下一个自然数的后继函数,以及归纳法原理——从本质上说,所有的自然数都源于 0,它们是通过反复对 0 应用后继函数得到的。
事实上,简单的要素也可以创造出极端的复杂性,这就是为什么所有的数学资源都被用于助力数论。在本章中,我们将讨论几何、代数和微积分对数论中的证明的影响,以及反过来的情况,特别是针对代数的情况。之后,当谈到证明本身的数学研究时,我们将看到是什么使数论如此复杂。
01
数论中的几何与微积分
我们现在已经看到如何通过单位圆上的有理点来理解勾股数组,反过来又通过有理函数

得到圆的参数化。此外,我们已经看到这些方程给出了一个变量替换,可以使关于 x 和 的有理函数的积分有理化。
的有理函数的积分有理化。
了解圆函数 参数化圆的读者或许想知道它与这个故事的关系。答案是参数t 和 θ 通过等式
参数化圆的读者或许想知道它与这个故事的关系。答案是参数t 和 θ 通过等式 联系起来。这可以从用于得到方程(*)的直线和圆的图中看出,见图 7.3。
联系起来。这可以从用于得到方程(*)的直线和圆的图中看出,见图 7.3。

一方面,我们知道

另一方面,根据正弦和余弦的定义,

那么,根据基本的几何(等腰三角形、三角形的内角和为 π ),我们发现角 OPR 为 。因此,红色直线的斜率 t 是 tan
。因此,红色直线的斜率 t 是 tan 。
。
虽然有理函数通常比超越函数(如正弦函数和余弦函数)更受欢迎,但当我们遇到无法由有理函数参数化的曲线(如 )时,后者是参数化的更好选择。为了了解如何处理这些曲线,我们回顾一下圆和圆函数在微积分中的作用。
)时,后者是参数化的更好选择。为了了解如何处理这些曲线,我们回顾一下圆和圆函数在微积分中的作用。
02
圆和其他曲线的微积分
如果 是一条形如
是一条形如 的曲线,这里的
的曲线,这里的 是一个多项式,那么有一个令人惊讶的简单方法可以找到
是一个多项式,那么有一个令人惊讶的简单方法可以找到 的参数化函数对。此外,如果
的参数化函数对。此外,如果 ,那么
,那么 (f 的导数)。其想法是考虑积分
(f 的导数)。其想法是考虑积分

这样做之后,显然有 ,而且有
,而且有

对于单位圆 的情况,多项式
的情况,多项式 ,定义函数
,定义函数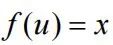 的积分是
的积分是

通过替换 ,很容易看到这个积分是
,很容易看到这个积分是 ,所以
,所以 ,于是
,于是 。最后,
。最后, ,于是我们得到参数化
,于是我们得到参数化

这与由圆函数给出的通常的参数化是相同的,只不过 x 和 y 进行了对换。
03
椭圆函数和椭圆曲线
上述参数化曲线 的方法只能得到我们已知的圆
的方法只能得到我们已知的圆 的参数化。该方法为曲线
的参数化。该方法为曲线 提供了一些新的想法。我们知道这条曲线不存在有理函数参数化,所以函数
提供了一些新的想法。我们知道这条曲线不存在有理函数参数化,所以函数 和
和 可能是有趣的。
可能是有趣的。
事实上,积分 是一个椭圆积分,正如第 6.9 节所提及的,函数
是一个椭圆积分,正如第 6.9 节所提及的,函数 和
和 被称为椭圆函数。事后来看,研究函数而不是其逆(积分)似乎是个好主意,因为研究正弦函数显然比研究反正弦积分更容易。
被称为椭圆函数。事后来看,研究函数而不是其逆(积分)似乎是个好主意,因为研究正弦函数显然比研究反正弦积分更容易。
然而,第一个关注椭圆函数而不是椭圆积分的数学家是高斯(大约在 1800 年,未发表),这是在法尼亚诺(Fagnano 1718)和欧拉(Euler,1751 年第一次看到法尼亚诺的成果)费力地得到椭圆积分的一些性质之后才发生的。椭圆函数的思想直到 19 世纪 20年代才被发表,当时被阿贝尔(Abel)和雅可比(Jacobi)重新发现。
高斯发现积分

的反函数 与正弦函数非常相似,以至于他称其为双纽线正弦函数。特别是,双纽线正弦函数具有周期性:对于某个最小的数
与正弦函数非常相似,以至于他称其为双纽线正弦函数。特别是,双纽线正弦函数具有周期性:对于某个最小的数 ,有
,有 高斯之所以选择字母
高斯之所以选择字母 ,是因为它是希腊字母
,是因为它是希腊字母 的变体。不仅如此,如果我们允许 u 是复数,那么 sl 有第二个周期
的变体。不仅如此,如果我们允许 u 是复数,那么 sl 有第二个周期 。我们知道,对于代数曲线,允许 x 和 y 为复数是很自然的。
。我们知道,对于代数曲线,允许 x 和 y 为复数是很自然的。
这种双周期性也适用于其他椭圆函数(但不适用于正弦函数和余弦函数,即使当我们允许它们为复变量时,它们仍然保持单周期)。这导致了对它们参数化的曲线的全新解释,称为椭圆曲线。
例如,下面展示了如何用笛卡儿方程 来看待曲线
来看待曲线 。
。 具有参数方程
具有参数方程

所以 上的每一点 P 都由参数 u 的值确定。但是,对任意整数 m 和 n,由于
上的每一点 P 都由参数 u 的值确定。但是,对任意整数 m 和 n,由于 (和
(和 )的周期性(具有相同周期),参数值
)的周期性(具有相同周期),参数值 确定的是相同的点。
确定的是相同的点。
这样,  上的每一点 P 对应于复平面
上的每一点 P 对应于复平面 中的一个点集
中的一个点集

我们可以从顶点为 的正方形中选择每个点集的一个代表元,在这种情况下,除了边界上的点外,每个点 P 在正方形中只有一个代表元。左右两边的点
的正方形中选择每个点集的一个代表元,在这种情况下,除了边界上的点外,每个点 P 在正方形中只有一个代表元。左右两边的点 表示
表示 上的同一点,上下两边的点
上的同一点,上下两边的点 也表示
也表示 上的同一点,因此,所有四个顶点
上的同一点,因此,所有四个顶点 都表示同一点。在图 7.4 中,左图的正方形是灰色的,左边和右边是蓝色,上边和下边是红色。
都表示同一点。在图 7.4 中,左图的正方形是灰色的,左边和右边是蓝色,上边和下边是红色。

粗略地说(或从拓扑上讲),复曲线 是将正方形的同色边粘贴的结果,也就是所谓的环面。因此,寻找曲线上有理点的过程不仅涉及几何学和微积分,而且涉及拓扑学。
是将正方形的同色边粘贴的结果,也就是所谓的环面。因此,寻找曲线上有理点的过程不仅涉及几何学和微积分,而且涉及拓扑学。
推荐阅读

《证明的故事:从勾股定理到现代数学》
作者:[澳] 约翰·史迪威(John Stillwell)
译者:程晓亮 张浩
数学史泰斗、旧金山大学荣休教授,“肖夫内奖”获得者,当今世界最有影响力的数学家之一约翰·史迪威全新力作!
证明是数学思想中十分重要且极具开拓性的特征之一。没有证明,就没有真正的数学!
本书从古希腊几何学时代讲起,涵盖代数、微积分、集合、数论、拓扑、逻辑等几乎全部数学分支中的证明故事,讲述了证明的演变及其在数学中的重要作用和启发意义。我们将看到欧几里得、康托尔、哥德尔、图灵等数学大师的精彩发现和发明。
本书不是教材,而是在讲数学的历史,更是在讲数学思想的演变。
配套阅读

《基础数学讲义:走向真正的数学》
作者:(英) 伊恩·斯 图尔特 (Ian Stewart) 、(英) 戴维·托尔
译者:姜喆
数学畅销书作家伊恩•斯图尔特 X 数学思维发展和教育家戴维·托尔
合力打造高等数学入门经典巨作。
在数学学习的道路上走向“成熟”
弥合中学与大学数学学习的差距
一本被美国大学广泛采用的参考书
启发思维,有效引导,知识与方法深度结合
























 24
24

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








