1. 符号说明
nl
:表示网络的层数,第一层为输入层
sl
:表示第l层神经元个数
f(·) :表示神经元的激活函数
W(l)∈Rsl+1×sl
:表示第l层到第l+1层的权重矩阵
b(l)∈Rsl+1
:表示第l层到第l+1层的偏置
z(l)∈Rsl
:表示第l层的输入,其中
zi(l)
为第l层第i个神经元的输入
a(l)∈Rsl
:表示第l层的输出,其中
ai(l)
为第l层第i个神经元d的输出
2. 向前传播
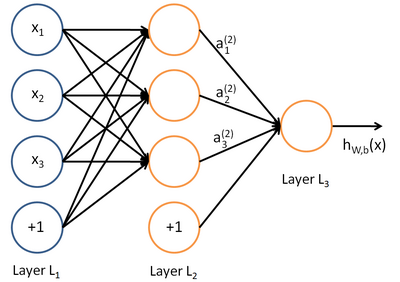
下图直观解释了层神经网络模型向前传播的一个例子,圆圈表示神经网络的输入,“+1”的圆圈被称为偏置节点。神经网络最左边的一层叫做输入层,最右的一层叫做输出层。中间所有节点组成的一层叫做隐藏层。
每个神经元的表达式如下:
前向传播的步骤如下:
z(l)=W(l−1)a(l−1)+b(l−1)a(l)=f(z(l))⎫⎭⎬⎪⎪⇒z(l)=W(l−1)f(z(l−1))+b(l−1)
3. 反向传播算法推导过程
(1)目标函数
给定一个包含m个样本的训练集,目标函数为:
J(W,b)=1m∑mi=1J(W,b;x(i),y(i))+λ2∥W∥22
=1m∑mi=1(12∥h(x(i))−y(i))∥22)+λ2∑nl−1l=1∑sli=1∑sl+1j=1(Wji(l))2
采用梯度下降方法最小化J(W,b), 参数更新方式如下:
Wnew(l)=W(l)−α⋅∂J(W,b))∂W(l)
=W(l)−α∑mi=1∂J(W,b;x(i),y(i))∂W(l)−λW
bnew(l)=b(l)−α⋅∂J(W,b))∂b(l)
=b(l)−α∑mi=1∂J(W,b;x(i),y(i))∂b(l)
因此,参数更新的关键在于计算 ∂J(W,b;x,y)∂W(l) 和 ∂J(W,b;x,y)∂b(l)
(2)计算 ∂J(W,b;x,y)∂W(l)
根据链式法则可得:
∂J(W,b;x,y)∂W(l)=(∂J(W,b;x,y)∂z(l+1))T∂z(l+1)∂W(l)
其中, ∂z(l+1)∂W(l)=∂[W(l)⋅a(l)+b(l)]∂W(l)=a(l)
定义残差为: δ(l)=∂J(W,b;x,y)∂z(l)
对于输出层(第 nl 层),残差的计算公式如下:(其中, f(z(nl)) 是按位计算的向量函数,因此其导数是对角矩阵)
δ(nl)=∂J(W,b;x,y)∂z(nl)
=∂12∥h(x)−y)∥22∂z(nl)
=∂12∥f(z(nl))−y)∥22∂z(nl)
=(a(nl)−y)⋅diag(f′(z(nl)))
=(a(nl)−y)⊙f′(z(nl))
对于网络其它层,残差可通过如下递推公式计算:
δ(l)=∂J(W,b;x,y)∂z(l)
=∂a(l)∂z(l)∂z(l+1)∂a(l)∂J(W,b;x,y)∂z(l+1)
=∂f(z(l))∂z(l)⋅∂[W(l)a(l)+b(l)]∂a(l)⋅δ(l+1)
=diag(f′(z(l)))⋅(W(l))T⋅δ(l+1)
=f′(z(l))⊙(W(l))Tδ(l+1)
(3)计算 ∂J(W,b;x,y)∂b(l)
与(2)计算过程同理
∂J(W,b;x,y)∂b(l)=∂z(l+1)∂b(l)∂J(W,b;x,y)∂z(l+1)
=∂[W(l)⋅a(l)+b(l)]∂b(l)δ(l+1)
=δ(l+1)
综上所述:
∂J(W,b;x,y)∂W(l)=(δ(l+1))Ta(l)
∂J(W,b;x,y)∂b(l)=δ(l+1)
反向传播算法的含义是:第l 层的一个神经元的残差是所有与该神经元相连的第l+ 1 层的神经元的残差的权重和,然后在乘上该神经元激活函数的梯度。
4. 反向传播算法流程
借网上一张图,反向传播算法可表示为以下几个步骤:








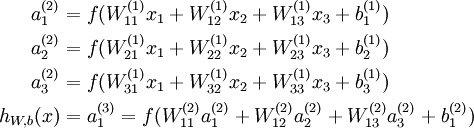

















 826
826

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








