贝叶斯定理

贝叶斯定理

　　观测，获取知识和进行预测是科学过程的基础。我们预测的准确性取决于我们目前知识的质量和观测的精度。天气预报是一个熟悉的例子，对于天气工作的原理，如果我们知道的越多，我们就能更好地利用当前的观察和季节性记录来预测明天是否会下雨，预测与观测之间的任何不同可用于改善天气模型。贝叶斯统计体现了应用先前的理论和经验知识来制定假设的这个循环，在观测数据的基础上对他们进行排名并用观测数据来更新先验概率估计和假设。本文我们讨论贝叶斯定理，对于扩展的主题，如贝叶斯推理和网络会后续给出.

贝叶斯统计经常与古典（频率论）统计做对比，古典统计假定观察到的现象由一个未知但固定的过程产生。重要的是，古典统计假设总体参数是未知的常数，因为关于样本空间完整并确切的知识无法获得。为估计总体特征，概率的概念被用来描述测量的结果.

与此相反，贝叶斯统计假设总体参数是量化的随机变量，关于它们的不确定性可通过概率分布进行描述。我们做参数的主观概率陈述或“先验”，这些参数是基于我们的经验和总体推理。从这个角度概率可理解为所研究的参数值信念的度量。一旦我们收集到数据，我们将其与先验组合来创建一个名为后验的分布，该分布代表参数的最新信息，并将其作为参数可能值的概率评估。由于经验，知识和推理过程因人而异，所以他们的先验也一样，贝叶斯统计中最有争议的话题之一就是制定先验的规格。但是，先验的影响通常会随着我们收集知识和获得观察而减少。

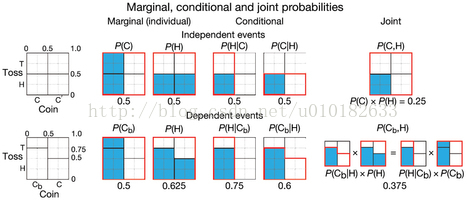
贝叶斯统计学的核心是贝叶斯定理，它利用条件概率的概念，描述了相关（依赖）事件的结果概率。为了说明这些概念，我们先从独立事件开始，投掷两个相同的硬币，C和C'。投掷的结果概率不依赖于硬币的选择-头的概率总是相同的，P（H）=0.5（图1）。选择一个给定硬币（例如，C）的联合概率和投掷的结果（例如，H）是简单的单个概率乘积，P（C，H）= P（C）×P（H）。但是，如果我们用一个偏置的硬币代替一个硬币，Cb，它能产生头的概率是75％，硬币的选择将影响投掷结果概率，使得事件具有依赖性。我们用条件概率P（H|C）=0.5和P（H|Cb）= 0.75来表达，其中，“|”表示“给定”或“在此条件上”（图1）。

图1.独立和相关事件的边缘，联合和条件概率。概率用平面图展示，其中列对应硬币和列中的分段条形图对应抛硬币的结果，并由蓝色区域与红色轮廓面积的比率给出。两个硬币的选择和投掷的结果是独立事件。对于独立事件，边缘和条件概率是相同的，联合概率用概率的乘积来计算。如果一个硬币，Cb，是偏置的（产生头（H）的概率是75％），那么事件是相关的，并且联合概率用条件概率来计算。

　　如果P（H | Cb）是观察头出现的概率，那么我们该怎么计算P（Cb| H）的概率呢？这两个条件概率通常是不一样的。 P（H |Cb）是偏硬币的一个属性，不像P（Cb|H），它是不受硬币是偏置这种情况的影响。

　　我们通过写出Cb和H的联合分布来关联这些条件概率：P（Cb，H）=P（Cb| H）×P（H）（图1）。它是对称的：P（Cb| H）×P（H）= P（H |Cb）×P（Cb），这个事实指导我们到贝叶斯定理，这是等式的一个重新整理：P（Cb| H）= P（H | Cb）×P（Cb）/ P（H）（图2a）。 P（Cb）是收集数据（先验）之前我们对硬币偏置的猜测，P（Cb| H）是一旦观测到头（后验）我们的猜测。

图2.贝叶斯定理及其概率迭代估计应用的图形解释。 （a）由贝叶斯定理（与硬币是偏置的假设相关P（Cb））给出的条件概率和一旦观测到数据它的概率P（Cb| H）之间的关系。 （b）选择硬币一致的概率可以从投掷的结果来推断。观察到头朝上的次数增加了硬币偏置的机会，P（Cb）从 0.5到0.6，并且如果第二次还是头朝上，那么该值进一步增加到0.69。

　　如果两个硬币被选中的概率一样即P（Cb）= P（C）=0.5。我们还知道，P（H |Cb）= 0.75，这是偏置硬币的一个属性。应用贝叶斯定理，我们需要计算的P（H），这是观察到头出现的概率（取一般的硬币并观察头出现的次数；取有偏置的硬币并观察头出现的次数）。P（H）= P（H | C）×P（C）+ P（H | Cb）×P（Cb）=0.5×0.5+0.75×0.5=0.625。通过代入这些值到贝叶斯定理，我们可以计算出观测到头朝上后是偏置硬币的概率，P（Cb| H）= P（H |Cb）×P（Cb）/ P（H）=0.75×0.5 /0.625= 0.6（图2a）。

　　贝叶斯定理可以迭代地应用到这样的逆概率问题---当我们获得数据后，需要一步一步地更新概率。举例来说，如果我们第二次抛硬币，我们可以更新硬币是偏置的预测。在第二个投掷中，我们不再使用P（Cb）= 0.5，因为第一次投掷表明偏置硬币更容易被选取。从第一投掷的后验成为新的先验，P（Cb）= 0.6。如果第二投掷产生头，我们计算P（H）=0.5×0.4+0.75×0.6=0.65并运用贝叶斯定理再次求P（Cb| HH）=0.75×0.6/0.65=0.69（图2B）。我们可以继续投掷来改善我们的猜测---每一次我们观察到头，硬币是偏置的后验概率的评估就会增加。举例来说，如果我们在一排看到四个头，那么硬币是偏置的后验概率是84％（见http://download.csdn.net/my/uploads）。

　　我们已计算出给定观测两个头后硬币是偏置的概率。到现在为止，我们还没有进行任何统计推断，因为所有的概率已被指定。贝叶斯和频率论都认为，P（Cb| HH）=0.69和P（HH| C）=0.25。当有一个未知时，如P（H|Cb），统计推断就出现了。频率论和贝叶斯推理之间的不同将会在以后更充分的讨论。

　　让我们扩展简单的硬币例子到包含多个事件结果。假设一个患者有三种疾病（X，Y，Z）中的一种，三种疾病的患病率分别是0.6，0.3或0.1---X是比较普遍的，而Z是罕见的。我们可以使用一个诊断测试来测量蛋白质标志物（A，B）的存在。两种标记在疾病中都存在，并且对于每种疾病观察到给定标志物的概率是已知的，每一种疾病（图3a）是相互独立的。我们可以问：如果我们看到一个标志A，我们可以预测患者的状态吗？此外，如果我们之后对B进行分析，我们的预测该如何改变？

　　我们首先计算出病人给定标记A患X疾病的概率：P（X | A）= P（A | X）×P（X）/ P（A）。我们知道X的先验概率，P（X）= 0.6，给定X观察到A的概率，P（A |X）= 0.2（图3a中）。应用贝叶斯定理我们需要计算P（A），它是观察到A的概率并且不管病人是什么状态。为了找到P（A），我们相加每一种疾病的概率和对应疾病中找到A的乘积：P（A）= 0.6×0.2 + 0.3×0.9 + 0.1×0.2 = 0.41（图3b）。根据贝叶斯定理我们得到P（X | A）= 0.2×0.6 / 0.41 = 0.29。因为标记A是在另一种疾病Y中比较普遍，该患者具有疾病X的估计比原来的0.6要低得多。同样，我们可以计算出Y和Z的后验P（Y | A）= 0.66和P（Z | A）= 0.05（见http://download.csdn.net/my/uploads）。用单个测定证实A，最有可能（66％）患者有疾病Y。

图3.基于标记存在的疾病预测。（a）给定一个疾病（X,Y,Z），观察到每个标记（A,B）的独立条件概率（例如，P（A| Y）=0.9）。 （b）给定单个观察，每个疾病的后验概率（例如，P（Y| A）=0.66）。 （c）多个分析的疾病概率预测演化。对于给定的疾病，每个路径追踪（左到右）后验的值。从疾病的先验开始（蓝点）到合并所有的分析结果。分析结果用一个空（标记不存在）或固体（标记存在）点编码。红色的路径对应于A和B。最高可能的后验概率用粗体显示。

　　相反，如果我们确认B是出现的，X，Y和Z中的概率分别是44％，22％和33％，（图3b），而我们最好的猜测是该患者患X，即使标记B几乎总是存在Z中---P（B | Z）= 0.9，检测到它只提高了Z的概率到P（Z | B）= 0.33，这仍比X的概率低，原因是Z本身是罕见的，并且在较常见的疾病X和Y中观察的B也是可能的。这种现象用卡尔·萨根的话来说就是：“非凡的索赔要求非凡的证据。“在这种情况下，观察到B不够”非同凡响“以至于无法显著提高病人患Z的主张。即使B总是存在于Z中，即P（B | Z）= 1，并存在于X和Y中只有1％，P（B | X）= P（B | Y）= 0.01，观察到B只会让我们说有一个92％的机会病人患Z。如果我们没有考虑不同的患病率，我们将严重高估该患者患Z的机率。例如，如果我们假定这三种疾病发生的可能性一样，P（X）= P（Y）= P（Z）= 1/3，观察到B将导致我们相信Z的机会是69％

　　已经观察到A，我们可以通过测试B来完善我们的预测。我们使用观察到A后的后验概率作为新的先验。假定A和B都存在，对于疾病X,Y和Z的后验概率分别是0.25，0.56和0.19，Y是最有可能的。如果B的测试是负值，计算是相同的，但是使用互补概率（例如，P（not B| X）=1 - P（B| X）），并发现0.31，0.69和0.01为X，Y和Z的概率。观察到A而不是B极大减小了疾病Z的机率，从19％到1％。图3c跟踪带有每种可能结果的各个疾病的后验概率的变化，正如我们在指标之间轮流测试一样。如果我们既没发现A也没发现B，那么患者患X的概率是92％。Y的主要指定形状是A + B-（69％），Z是A-B+（41％）。

　　当事件的结果自然映射到条件概率，贝叶斯定理提供了一个推理和便捷计算的直观方法。它使我们能够结合先验知识与观测来做现象的预测。在贝叶斯推理中，系统中的所有未知数通过使用贝叶斯定理作为证据积累来更新的概率分布来建模。

参考文献

1. Eddy, S.R. Nat. Biotechnol. 22, 1177–1178 (2004).
2. Krzywinski, M. & Altman, N. Nat. Methods 10, 809–810 (2013).
3. O ldford, R.W. & Cherry, W.H. Picturing probability: the poverty of Venn diagrams,
the richness of eikosograms. http://sas.uwaterloo.ca/~rwoldfor/papers/venn/
eikosograms/paperpdf.pdf (University of Waterloo, 2006)