PRML-系列一之1.2

概率论
　　模式识别领域中一个关键概念是不确定性。通过噪声测量以及有限大小的数据集都会出现。概率论提供了不确定性量化和操纵统一的框架并形成模式识别的中心基础之一。当与决策论（在1.5节中讨论）结合时，给出所有可获得的信息，我们就能够得到最佳预测，即使这些信息可能不完整或不明确的。
　　我们通过考虑一个简单的例子来介绍概率论的基本概念。想象一下，我们有两个箱子，一红一蓝，红色箱子中我们有2个苹果和6个桔子，而在蓝箱子中，我们有3个苹果，1个桔子。如图1.9。现在假设我们随机选取一个箱子并从这个箱子中随机选一个水果，观察是何种水果后我们放回到原来的箱子里。我们可以想像重复该过程多次。假设就是这么做，我们挑红箱子的次数是40％，我们挑蓝箱子的次数是60％，而当我们从箱中取出一个水果时，等价地我们有可能选择了箱子中其余的所有水果。

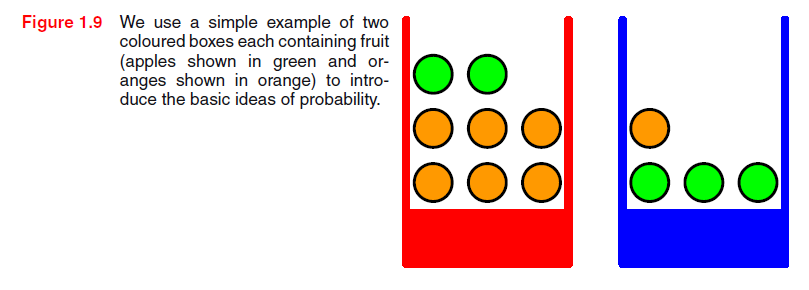
　　在这个例子中，选择箱子的身份是一个随机变量，我们用B表示。这个随机变量可以取两种可能值的一个，即r（对应于红箱子）或b（对应于蓝箱子）。同样地，水果的身份也是随机变量并用F表示。它取a（苹果）或o（橙色）的的任意一个。
　　首先，我们将定义事件概率为整个试验中事件发生的次数，在极限的状态下试验总次数趋于无穷大。因此，选择红色箱子的概率是4/10而选择蓝色箱子的概率是6/10。我们将概率写为p（B= r）=4/10，p（B = b）=6/10。注意，根据定义概率必须位于区间[0，1]上。此外，如果事件是相互排斥的并且包括所有可能的结果（例如，在本试验汇中箱子必须是红色或蓝色），那么我们可以看到这些事件的概率必须加起来和为1。
　　现在，我们可以提出这样的问题：“挑到一个苹果的总概率是多少？“，或者”假设我们已经选了桔子，那么我们选择的箱子是蓝色的概率是多少？“。我们可以回答这样的问题，以及在模式识别中与之相关的更复杂的问题，前提是我们具备了概率论的两个基本规则，分别是求和规则和乘积规则。获得了这些规则后，我们再回到水果箱子的例子。
　　为了推导概率的规则，考虑稍微更一般的例子。图1.10涉及两个随机变量X和Y（可以是上面考虑的箱子和水果变量）。我们将假设X可以取xi的任一个值，其中i =1，， ，M而Y可以取yj的任一个值，其中j =1，， ，L。考虑N次试验，我们采样变量X和Y，并让X取xi和Y取yj的试验次数用nij表示。此外，让X取xi的试验次数（与Y的值不相关）用ci表示，并且类似地让Y取yj的试验次数用rj表示。

　　X取值xi和Y取值yj的概率写作P（X =xi，Y = yj），它被称为X =xi和Y =yj的联合概率。它由落到i，j单元的点的数目给出，该单元占所有点的一部分，因此

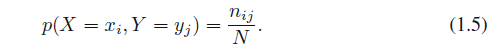
这里，我们正在隐含地考虑极限N→∞。同样，X取xi的概率写作p（X=xi）并且是由落在第i列的所有点得出的，使得

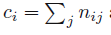
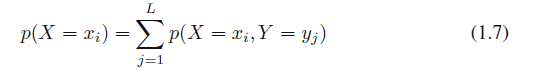
因为图1.10中i列的实例数量刚好是该列每个单元中实例数目的总和，所以我们有，因此，从（1.5）和（1.6），我们有

这是概率的加法规则。注意，ρ（X =xi）有时也被称为边缘概率，因为它是通过边缘化，或求和其他变量（在此情况下Y）得到的。
　　如果我们只考虑X=xi的实例，那么Y= yj的实例部分写做P（Y= yi| X=xi），它被称为给定X = xi，Y=yj的条件概率。通过找出第i列落在i，j单元的点可以得出，因此

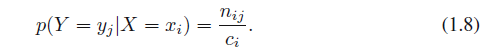
从（1.5）（1.6）和（1.8），我们可以得到下面的关系

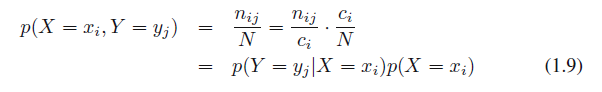
这是概率的乘积规则。
　　目前为止，我们已经十分仔细地得出了随机变量和随机变量所取值之间的区别。因此B取值r的概率表示为p（B=r）。虽然这有助于避免歧义，但是它产生了十分繁琐的符号。在许多情况下不需要这么教条。取而代之，我们可以简单地写p（B）表示随机变量B的一个分布，或者p（r）表示估计特定值r的分布，前提是上下文的解释很清晰。
　　用这个更加紧凑的符号，我们能重写概率论的两个基本规则

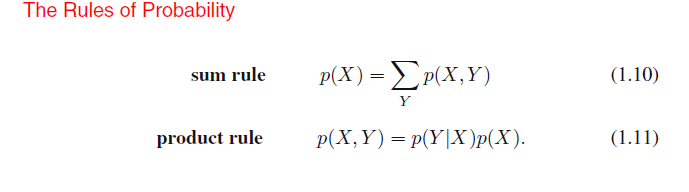
这里P（X，Y）是联合概率，并用语言表达为“X和Y的概率“。类似地，P（Y| X）是条件概率，并且语言表达为“给定X，Y的概率”，而P（X）是边缘概率，仅仅是“X的概率”。这两个简单的规则形成概率的基础，我们在整本书中都会使用到它。
　　从乘积规则，连同对称属性p（X，Y）= P（Y，X），我们立刻得到条件概率之间的关系

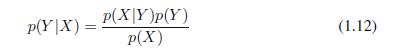
这被称为贝叶斯定理并在模式识别和机器学习中起很重要的作用。使用求和规则，贝叶斯定理中的分母可以用分子的数量和来表示

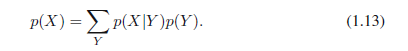
我们可以将贝叶斯定理中的分母看做归一化常数从而保证（1.12）左边的条件概率总和等于一。
　　在图1.11中，我们显示了涉及两个变量的联合分布例子来说明边缘和条件分布的概念。这里有限的N=60个数据点的样本已经从联合分布中描绘出来，并示于左上角。在右上角是每个Y值数据点的直方图。根据概率的定义，这部分在N→∞时应该等于相应的概率p（Y）。我们可以将直方图看做模拟概率分布的一种简单方法，只给出有限数量的描绘该分布点的数量。从数据中模拟分布是统计模式识别的心脏，在这本书会找到好多相关细节。图1.11中其余的两幅图显示ρ（X）和p（X |Y=1）的直方图估计。
　　现在我们回到水果箱的例子。就目前而言，我们应再次明确区别随机变量和他们的实例。我们已经看到，选择红色或蓝色的概率如下：

注意他们满足p（B=r）+p（B=b）=1。

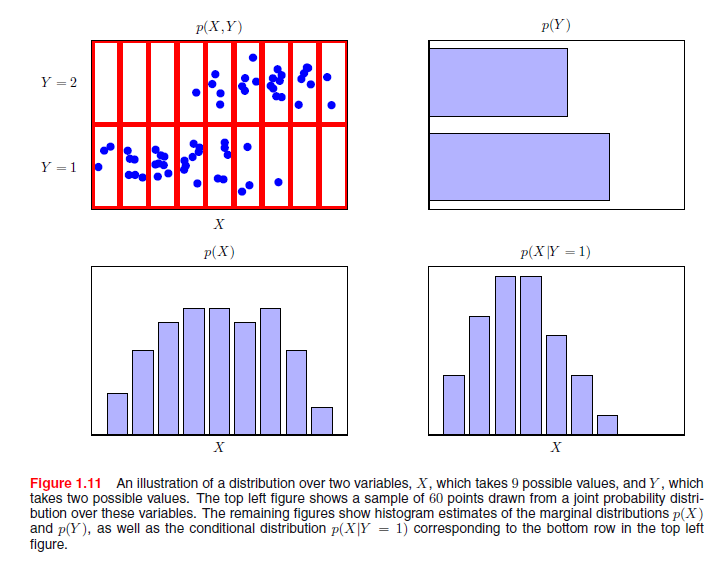
　　现在假设我们随机选择一个箱子，并且它是蓝箱子。然后取到一个苹果的概率只是在蓝箱子中苹果数即3/4，所以P（F = a | B= b）=3/4。事实上，我们可以写出水果类型的所有四个条件概率，假设已经选中一个箱子

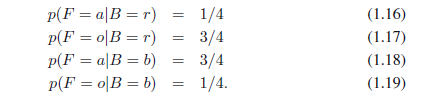
注意，这些概率被归一化了，所以

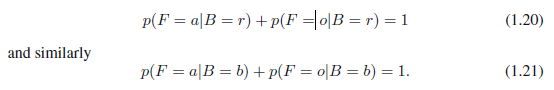
　　现在我们可以根据概率的求和和乘积规则来估计取出一个苹果的概率

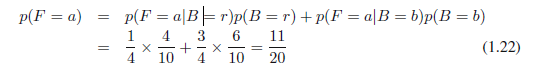
接着，应用求和规则，p(F = o) = 1 − 11/20 = 9/20。
　　相反，假设我们被告知已经选中了水果并且它是一个橙色，而我们想知道它来自哪个箱子。这要求我们估计水果作为条件箱子的概率分布，而（1.16） - （1.19）给出的是箱子作为条件水果的概率分布。通过使用贝叶斯定理，我们可以解决这个反转的条件概率问题

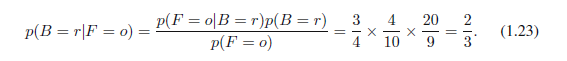
根据求和规则，p(B = b|F = o) = 1 − 2/3 = 1/3。
　　我们可以按如下提供贝叶斯定理的一个重要解释。如果我们要求箱子在取水果之前被告知，那么我们可用的最完整信息是由概率p（B）提供的。我们称这个为先验概率，因为它是我们观察到水果身份之前可用的概率。一旦我们被告知水果是桔子，那么我们就可以使用贝叶斯定理来计算p（B | F）的概率，我们称之为后验概率，因为它是我们观察到F之后得到的概率。.注意，在这个例子中，选择红箱子的先验概率是4/10，因此我们更可能选择蓝箱子而不是红箱子。然而，一旦我们已经观察到取出的水果是桔子，我们发现现在红色箱子的后验概率是2/3，从而使现在我们更可能选到红箱子。这一结果符合我们的直觉，因为红箱子中桔子的比例要比蓝箱子高得多，所以水果是桔子的观察值提供了显著的有利于红色箱子的证据。事实上，证据是足够强以至于它超过了先验并且更可能选择红盒子而不是蓝色的。
　　最后，我们注意到，如果两个变量的联合分布因子分解成边缘的乘积，使得p（X，Y）= p（X）p（Y），则X和Y是独立的。根据乘积规则，我们看到p（Y| X）= p（Y），所以给定X，Y的条件分布是独立于X的值。例如，在我们的水果箱例子中，如果每个盒子包含相同的苹果和桔子，则p（F | B）= p（F）中，以使选择的概率，也就是说，苹果与选择哪个箱子没有关系。