我们以线性代数的中心问题开启我们的航程:解决线性方程。最重要并且也是最简单的情况就是位置函数的数目等于方程的数目。现在我们有包含
n
个未知变量的
消元 第二个方程减去第一个方程的四倍。从而消去第二个方程中的 x ,只留下了关于
y 的方程:
(方程2)−4(方程1)−3y=−6(2)这样就得到 y=2 。然后 x 从第一个方程1x+2y=3 计算出来:
1x+2(2)=3x=−1(3)计算出来后, x,y 也应该满足第二个方程。代入得: 4×(−1)+5×2=6行列式 y=2 完全依赖于方程中的六个数。对于 y 存在一个公式(当然
x 也有),是两个行列式的比值:
y=∣∣∣1436∣∣∣∣∣∣1425∣∣∣=1⋅6−3⋅41⋅5−2⋅4=−6−3=2(4)如果你知道 2×2 方阵的行列式,那么它就没有那么神秘了。它同样给出了解 y=2 。同样利用行列式,我们可以求出 x :
x=∣∣∣3625∣∣∣∣∣∣1425∣∣∣=3⋅5−2⋅61⋅5−2⋅4=3−3=−1(5)
我们来比较这两种方法,考虑
n
非常大(在科学计算中
最好的办法是高斯消元法。这个算法一直被用于解决大型的方程组。以后的大部分例子都是
n=3
,这是看不出太大区别。方程
(2)(4)
基本使用相同的步骤得到
y=2
。之后通过回带到方程(3)中很快得出
x
。对于更大的
消去法的想法看起来很简单,通过几个例子就能掌握它。它是非常基础的内容,通过简化矩阵我们就能理解它。在此我想讲四点更深层次的内容:
线性代数带来了平面几何。在十维空间中可视化九维平面不太容易。而理解相交于十个方程解的那些平面更难。但是不见得是不可能的。在图1 中有两条直线,相交于点 (x,y)=(−1,2) 。线性代数将图像放到十维空间里,在这个空间里,我们的直觉不得不去想象其几何形状。
图1:左边是例子的单个解,中间和右边是奇异情况,分别是无解和多个解
现在考虑矩阵符号,将 n 个未知量表示成向量
x , n 个方程表示成Ax=b 。我们用消去矩阵乘以 A 得到上三角矩阵U 。这些步骤将矩阵 A 分解为L×U ,其中 L 是下三角矩阵:
首先我们需要介绍矩阵和向量以及乘法规则。每个矩阵都存在转置 AT 。这个矩阵还存在逆矩阵 A−1A=∣∣∣1425∣∣∣=∣∣∣1401∣∣∣∣∣∣102−3∣∣∣=L×U(6) 大部分情况下,消去法不会存在问题。矩阵可逆的话,方程 Ax=b 还有一个解。但是在特殊的情况下这种方法就被打破了,既可能是方程组的顺序出错(通过交换一笑就能产生),也可能是方程没有唯一解。如果将例子中的5换成8,就出现了奇异的情况:
1x+2y=34x+8y=6(7)消去法依然用第二个减去第一个的四倍,那么结果是:
(方程2)−4(方程1)0=−6对于 n 个方程组,我们希望粗略算出需要多少步消去运算。计算代价经常决定着模型的精度。一百个方程需要一百万步(乘法和减法)的三分之一。计算机可以很快地计算出来。在一百步之后,舍入误差就已经很明显了。(有些问题敏感,而有些不敏感)在不知道全部细节的情况下,我们想明白实际中出现的大型系统以及他们是如何被解决的。
之后我会尽可能有效的介绍消去算法。这个算法用于各种各样的应用中,同时,用矩阵的方式(系数矩阵








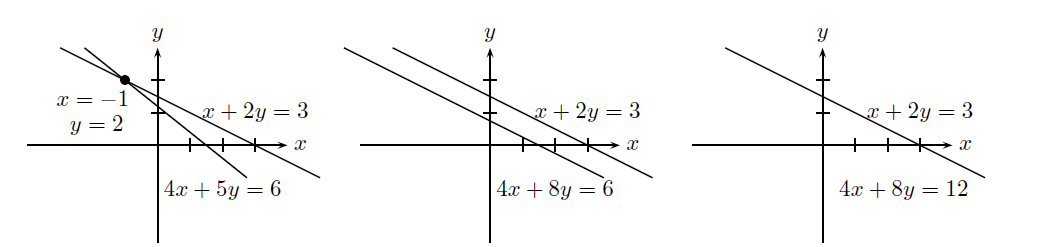

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








