漫步线性代数四——矩阵符号和矩阵乘法

对于$3\times 3$的例子，我们能够写出所有的公式。可以列出消去步骤，一个方程减去另一个方程的倍数达到三角矩阵的形式。对于一个大的系统，这种跟踪消去的步骤太长了，所以我们需要更加简洁的记录方式。

我们现在引进矩阵符号来描述开始的系统，用矩阵乘法来描述计算步骤会更简单。注意三种不同类型的量都出现在例子中：

$$\begin{equation} \begin{array}{lccccccc} {\rm{Nine\ coefficients\quad}}&2u&+&v&+&w&=&5\\ {\rm{Three\ unknowns\quad}}&4u&-&6v& & &=&-2\tag1\\ {\rm{Three\ right-hand\ sides\quad}}&-2u&+&7v&+&2w&=&9 \end{array} \end{equation}$$
右边是列向量 $b$。左边是未知量$u,v,w$。另外，左边有九个系数(其中一个碰巧是零)。自然地，我们用一个向量来表示三个未知量：
$${\rm The\ unknown\ is\ }x= \begin{bmatrix} u\\v\\w \end{bmatrix} \quad {\rm The\ solution\ is\ }x= \begin{bmatrix} 1\\1\\2 \end{bmatrix}$$
九个系数分为三行和三列，得到 $3\times 3$的矩阵：
$${\rm Coefficient\ matrix\quad }A= \begin{bmatrix} 2&1&1\\4&-6&0\\-2&7&2 \end{bmatrix}$$
$A$是一个方阵，因为方程个数等于未知量的个数。如果$n$个方程有 $n$个未知量，那么我们有$n\times n$矩阵。更一般地，可能 $m$个方程有$n$个未知量。那么 $A$是$m$行 $n$列的长方形。它将是一个$m\times n$矩阵。

矩阵互相相加，或乘以某个常数值，每一次执行一列的时候，效果和向量完全一样。事实上我们可以将向量看做矩阵的特殊情况；他们是只有一列的矩阵。和向量一样，如果两个矩阵形状相同时，他们才能执行加法：

$${\rm Additon\ A+B\quad} \begin{bmatrix} 2&1\\3&0\\0&4 \end{bmatrix} + \begin{bmatrix} 1&2\\-3&1\\1&2 \end{bmatrix}= \begin{bmatrix} 3&3\\0&1\\1&6 \end{bmatrix}$$
$${\rm Multiplication\ 2A\quad} \begin{bmatrix} 2&1\\3&0\\0&4 \end{bmatrix}= \begin{bmatrix} 4&2\\6&0\\0&8 \end{bmatrix}$$

矩阵和向量相乘

我们想用三个未知量$u,v,w$重写方程，得到简化的矩阵形式$Ax=b$。全写出来就是，矩阵乘以向量等于向量：

$$\begin{equation} {\rm Matrix\ form\ Ax=b\quad} \begin{bmatrix} 2&1&1\\4&-6&0\\-2&7&2 \end{bmatrix} \begin{bmatrix} u\\v\\w \end{bmatrix}= \begin{bmatrix} 5\\-2\\9 \end{bmatrix}\tag2 \end{equation}$$
右边 $b$是非齐次项列向量。左边是$A\times x$。我们准确的定义这个乘法以便于它能够重现最初的系统。 $Ax$的第一项来自 $A$的第一行乘以列向量$x$；
$$\begin{equation} {\rm Row\ times\ column\quad} \begin{bmatrix} 2&1&1 \end{bmatrix} \begin{bmatrix} u\\v\\w \end{bmatrix}= \begin{bmatrix} 2u+v+w \end{bmatrix} =\begin{bmatrix}5\end{bmatrix}\tag3 \end{equation}$$
乘积 $Ax$的第二部分是 $4u-6v+0w$，来自于 $A$的第二行。矩阵方程$Ax=b$等价于方程(1)中三个联立的方程组。

行乘列是所有矩阵乘法的基础。两个向量相乘得到一个数。这个数称为两个向量的内积。换句话说，$1\times n$矩阵(行向量)和$n\times 1$矩阵(列向量)相乘得到一个$1\times 1$矩阵：

$${\rm Inner\ product\quad} \begin{bmatrix} 2&1&1 \end{bmatrix} \begin{bmatrix} 1\\1\\2 \end{bmatrix}= \begin{bmatrix} 2\cdot 1+1\cdot 1+1\cdot 2 \end{bmatrix}= \begin{bmatrix}5\end{bmatrix}$$
这表明给出的解 $x=(1,1,2)$满足第一个方程。

矩阵$A$和一个向量$x$相乘有两种方法。一种方法是一次乘以一行，$A$的每行和$x$结合给出$Ax$的一部分。当$A$有三行是，存在三个内积：

$$\begin{equation} {\rm Ax\ by\ rows\quad} \begin{bmatrix} 1&1&6\\3&0&1\\1&1&4 \end{bmatrix} \begin{bmatrix} 2\\5\\0 \end{bmatrix}= \begin{bmatrix} 1\cdot 2+1\cdot 5+6\cdot 0\\ 3\cdot 2+0\cdot 5+3\cdot 0\\ 1\cdot 2+1\cdot 5+4\cdot 0 \end{bmatrix}= \begin{bmatrix}7\\6\\7\end{bmatrix}\tag4 \end{equation}$$
通常这就是$Ax$的解释，但是第二种方法同样重要。事实上，它更重要！它是一次乘以一列。$Ax$乘积一下就计算出来，就像矩阵$A$三列的组合：
$$\begin{equation} {\rm Ax\ by\ clumns\quad} 2\begin{bmatrix} 1\\3\\1 \end{bmatrix} +5\begin{bmatrix} 1\\0\\1 \end{bmatrix} +0\begin{bmatrix} 6\\3\\4 \end{bmatrix}= \begin{bmatrix} 7\\6\\7 \end{bmatrix}\tag5 \end{equation}$$
答案就是两倍的第1列加5倍的第2列。它对应于线性方程组的列图像。如果右边$b$是7,6,7，那么解就是2,5,0。当然行图像也是如此(我们最终要做相同的乘法)。

列规则将会一遍又一遍的使用，现在我们在强调一遍：

1、$Ax$的乘积可以利用方程(5)中的列找出来，因此$Ax$ 是$A$列的组合，其中系数是$x$的元素。

为了让$A\times x$在$n$维空间中，我们需要一个符号来表示$A$的每一项。第$i$行，第$j$列的元素用$a_{ij}$表示。第一个下标给出行数，第二个下标指示列。(在方程(4)中，$a_{21}$是3，$a_{13}$是6)如果$A$是一个$m\times n$矩阵，然后索引从1到$m$-有$m$行，索引$j$从1到$n$。合在一起，矩阵有$mn$个元素并且$a_{mn}$位于右下角。

一个下标对向量来说已经足够了。$x$的第$j$个元素用$x_j$ 表示。(以上的乘法有$x_1=2,x_2=5,x_3=0$)通常$x$写成列向量，就像$n\times 1$矩阵。但有时它写成一条线，如$x=(2,5,0)$。括号和逗号强调它不是$1\times 3$矩阵。而是一个列向量，它只是暂时躺着而已。

为了描述乘积$Ax$，我们使用“sigma”符号求和$\Sigma$表示和：

$${\rm Sigma\ notation\qquad} {\rm The}\ i{\rm th\ component\ of\ }Ax\ {\rm is}\sum_{j=1}^na_{ij}x_j$$
这个和取 $A$的第$i$行。索引 $j$取1到$n$的所有值，然后将结果加起来-和就是 $a_{i1}x_1+a_{i2}x_2+\cdots+a_{in}x_n$。

我们再次见到行的长度( $A$的列数)必须匹配$x$的长度。一个$m\times n$矩阵乘以$n$维向量(得到$m$维向量)。求和符号比啥都写满简单许多，但是矩阵符号要更好。(爱因斯坦用“张量符号”，其中重复的索引意味着求和。他写$a_{ij}x_j$ 或$a_i^jx_j$，我们不是爱因斯坦，所以保持用符号$\Sigma$)

消元的矩阵形式

到目前为止，对方程组，我们有一种方便速记的形式$Ax=b$。 那么在消元过程中是怎么进行操作的呢？在我们的示例中，第一步是中用第二个方程减去第一个方程的2倍。对于右边就是，$b$的第二个元素减去第一个元素的2倍。如果我们用初等矩阵(或消元矩阵)乘以$b$，会取得同样的效果：

$${\rm Elementary\ matrix\quad}E= \begin{bmatrix} 1&0&0\\-2&1&0\\0&0&1 \end{bmatrix}$$
根据矩阵和向量乘法的规则得以证实：
$$Eb= \begin{bmatrix} 1&0&0\\-2&1&0\\0&0&1 \end{bmatrix} \begin{bmatrix} 5\\-2\\9 \end{bmatrix}= \begin{bmatrix} 5\\-12\\9 \end{bmatrix}$$
5和9保持不变(因为 $E$的行1,0,0和0,0,1)。第一次消元步骤后，得到新的第二个元素-12。

它很容易用矩阵$E$描述，它单独执行消元步骤。我们也注意到“单位矩阵”，不执行任何操作。

2、单位矩阵$I$主对角线上为1，其余地方为0，不改变向量的值。基本矩阵$E_{ij}$表示第$i$行减去$\ell$倍的$j$行。$E_{ij}$包含第$i$行第$j$列的$-\ell$。

$$I= \begin{bmatrix} 1&0&0\\0&1&0\\0&0&1 \end{bmatrix} {\rm has}\ Ib=b\qquad E_{31}= \begin{bmatrix} 1&0&0\\0&1&0\\-\ell&0&1 \end{bmatrix} {\rm has}\ E_{31}b= \begin{bmatrix} b_1\\b_2\\b_3-\ell b_1 \end{bmatrix}$$
$Ib=b$类似于乘1运算。典型的消元步骤是$E_{31}$。重要的问题是：左边的$A$发生了什么？

为了保持相等，$Ax=b$两边必须使用相同的操作。换句话说，我们也必须用矩阵$E$乘以向量$Ax$。我们最初的矩阵$E$从第二行减去第一行的2倍，这一步之后，新的简单方程组(等价于旧的)就是$E(Ax)=Eb$。因为第一个主元下面都是零，所以它更简单。因为我们可以恢复到最初的方程组(通过第二行加上第一行的2倍)所以他们是等价的。所以这两个方程组具有完全相同的解$x$。

矩阵乘法

现在我们来看最重要的问题：我们如何计算两个矩阵相乘？我们可以从高斯消元法中得到部分线索：我们知道最初的系数矩阵$A$，消元矩阵$E$，而且还知道消元后的结果$EA$。我们希望并期望

$$E= \begin{bmatrix} 1&0&0\\-2&1&0\\0&0&1 \end{bmatrix} {\rm times}\ A= \begin{bmatrix} 2&1&1\\4&-6&0\\-2&7&2 \end{bmatrix} {\rm gives}\ EA= \begin{bmatrix} 2&1&1\\0&-8&-2\\-2&7&2 \end{bmatrix}$$
矩阵$A$的第二行减去第一行的两倍。矩阵乘法和消元法的行操作比较一致。我们可以将结果写成$E(Ax)=Eb$或$(EA)x=Eb$。 精确地构造矩阵$EA$使得方程成立，括号不是必须的：
$${\rm Matrix\ multiplication\quad}(EA \times x){\rm equals}(E\times Ax)\quad {\rm We\ just\ write\ }EAx$$
这是”结合律”，就像$2\times (3\times 4)=(2\times 3)\times 4$。交换律似乎显而易见，所以很难想象它可能是错的。但是“交换律”$2\times 3=3\times 2$对于矩阵来说就不成立$EA\neq AE$。

关于矩阵乘法还有另一项要求。我们知道如何计算$Ax$，一个矩阵和一个向量，新的定义应该也使它满足。当矩阵$B$只包含一个列$x$时，矩阵与矩阵$AB$的乘积应该和矩阵与向量的乘积$Ax$相同。更重要的是：当$B$包含几列$b_1,b_2,b_3$时，$AB$的列应该是$Ab_1,Ab_2,Ab_3$！

$${\rm Multiplication\ by\ columns\qquad} AB= A\begin{bmatrix} b_1\\b_2\\b_3 \end{bmatrix} =\begin{bmatrix} Ab_1\\Ab_2\\Ab_3 \end{bmatrix}$$

我们的第一个要求与行有关，而这个与列有关。$A$的第三种方法是描述$AB$的每一项。事实上，只有一个可能的规则，不知道是谁发现了它，它恒成立，因为这个规则，我们不用让每对矩阵相乘。如果他们是方形的，他们肯定有相同的大小。如果是矩形的，他们形状肯定不一样；$A$的列数必须等于$B$的行数。然后$A$ 可以成$B$的每一列。

如果$A$是$m\times n$，$B$是$n\times p$，那么可以做乘法。乘积$AB$是$m\times p$。现在我们找出$AB$$i$行$j$列的元素。

3、$AB$的$i,j$项是$A$的第$i$行与$B$的第$j$列的内积。在图1中，$AB$的第3,2项从3行，2列计算得到：

$$\begin{equation} (AB)_{32}=a_{31}b_{12}+a_{32}b_{22}+a_{33}b_{32}+a_{34}b_{42}\tag6 \end{equation}$$

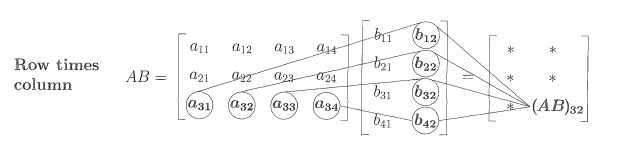
图1： $3\times 4$的矩阵 $A$乘以$4\times 2$的 矩阵 $B$得到$3\times 2$的矩阵 $AB$

注意，当矩阵没有经过消元处理时我们写成$AB$。因为初等矩阵$E$，所以我们前面的示例中写成$EA$。之后我们有$PA$或$LU$或$LDU$。矩阵乘法的规则都是一样。

例1：

$$AB= \begin{bmatrix} 2&3\\4&0 \end{bmatrix} \begin{bmatrix} 1&2&0\\5&-1&0 \end{bmatrix}= \begin{bmatrix} 17&1&0\\4&8&0 \end{bmatrix}$$
$17$就是$(2)(1)+(3)(5)$，$A$的第一行与$B$的第一列内积的结果。$8$就是$(4)(2)+(0)(1)$，$A$的第二行与$B$的第二列内积的结果。

$B$的第三列是零，所以$AB$也是零。$B$包含三列，$B$分别乘以每一列。$AB$的每一列都是$A$列的组合。就像矩阵和向量乘法一样，$A$列的系数就是$B$中的元素。

例2：

$${\rm Row\ exchange\ matrix\qquad} \begin{bmatrix} 0&1\\1&0 \end{bmatrix} \begin{bmatrix} 2&3\\7&8 \end{bmatrix}= \begin{bmatrix} 7&8\\2&3 \end{bmatrix}$$

例3：单位矩阵$I$不改变任何矩阵：

$${\rm Identity\ matrix\qquad} IA=A\quad {\rm and}\quad BI=B$$

重要提示：乘法$AB$也可以一次计算一行。在例中1中，$AB$ 的第一行可以使用$A$第一行的数字2和3。这些数字给出$2[row\ 1]+3[row\ 2]=[17\ 1\ 0]$。就像之前的消元法，$AB$ 的每行是$B$行的组合。

4、(1)$AB$的元素是行和列的乘积：

$$(AB)_{ij}=(row\ i\ of\ A)\times (column\ j\ of\ B)$$
(2)$AB$的每一列是矩阵和列的乘积：
$$column\ j\ of\ AB=A\times (column\ j\ of\ B)$$
(3)$AB$的每一行是行和矩阵的乘积：
$$row\ i\ of\ AB=(row\ of\ A)\times B$$

这引出了矩阵乘法的一个关键性质。假设三个矩阵$A,B,C$的形状(可能是矩形)可以加倍，$A,B$的行乘以$B,C$的列，那么关键性质就是：

5、矩阵乘法满足结合律：$(AB)C=A(BC)$，写作$ABC$。

$AB\times C=A\times BC$。如果$C$刚好是一个向量(只有一列的矩阵)，这正好就是之前提到的$(EA)x=E(Ax)$，这是矩阵乘法规则的基础。如果$C$有几列，我们可以一列列考虑，所利用几次法则。当计算几个矩阵乘法时，括号是没必要的。

还有两个性质需要提到-一个是矩阵乘法满足的，另一个是它不满足的。

6、矩阵乘法满足分配律：
$A(B+C)=AB+AC\quad and\quad (B+C)D=BD+CD$

当然这些矩阵的形状必须匹配-$B,C$有相同的形状，这样的话他们才可以相加。这个定律的证明太过无聊这里不再陈述。

下面这条性质就不满足了：

7、矩阵乘法不满足交换律：通常\ $FE\neq EF$

例4：假设$E$是第二行减去第一行的2倍，$F$是第一行加到第三行上：

$$E= \begin{bmatrix} 1&0&0\\-2&1&0\\0&0&1 \end{bmatrix} {\rm \quad and\quad}F= \begin{bmatrix} 1&0&0\\0&1&0\\1&0&1 \end{bmatrix}$$
两个矩阵相乘得：
$$EF= \begin{bmatrix} 1&0&0\\-2&1&0\\1&0&1 \end{bmatrix} =FE$$
无论是哪种顺序 $EF$或 $FE$，利用第一行改变了第二和第三行的值。

例5：假设$E$和上面一样，但$G$是第二行加到第三行上。现在改变他们的顺序，当先执行$E$，再执行$G$，在改变第三行之前第二行已经改变了。如果反过来，那么第三个等式不会受到第一行的影响，我们将会看到$EG$的(3,1)元素为零，而$GE$的是-2：

$$EF= \begin{bmatrix} 1&0&0\\0&1&0\\0&1&1 \end{bmatrix} \begin{bmatrix} 1&0&0\\-2&1&0\\0&0&1 \end{bmatrix}= \begin{bmatrix} 1&0&0\\-2&1&0\\-2&1&1 \end{bmatrix} \quad but\quad EG= \begin{bmatrix} 1&0&0\\-2&1&0\\0&1&1 \end{bmatrix}$$
因此 $EG\neq GE$。随便举个例子依然如此(大部分矩阵都不满足)。这里的矩阵是有意义的， $EF=FE$而 $EG\neq GE$是有原因的，我们有必要看看三个消元矩阵放一起会发生什么：
$$GEF= \begin{bmatrix} 1&0&0\\-2&1&0\\-1&1&1 \end{bmatrix} \quad and\quad EFG= \begin{bmatrix} 1&0&0\\-2&1&0\\-1&1&1 \end{bmatrix}$$
$GFE$是消元的正确顺序。将最初的矩阵 $A$变成了上三角矩阵$U$，我会在下一篇文章中再次讲述。

其他矩阵$EFG$更好。对于这个顺序，$E$的-2，$F$的1和 G <script type="math/tex" id="MathJax-Element-369">G</script> 都未受到影响，他们直接得出乘积，而它却是错误的消元顺序。但幸运的是，它是右边消元步骤的逆(我也会在下一篇文章里讲解)。

注意，下三角矩阵的乘积依然是下三角矩阵。