漫步线性代数十一—— 四个基本子空间

上篇文章处理了定义而不是，我们知道基是什么，但不知道如何找到他们。现在，从一个明确描述的子空间开始，我们开始计算显式的基。

子空间能用两种方式描述。第一，我们可以给出一个生成空间的向量集合。(例如：列生成列空间)第二，我们可以给出空间中的向量必须满足什么条件。(例如：零空间包含满足$Ax=0$ 的所有向量)

第一个描述可能包含无用的向量(相关列)，第二个描述可能包含重复的条件(相关行)，我们无法通过观察写出一个基，那么就需要一个系统的过程。

读者能够猜出来那个过程发生了什么，当在$A$上执行消元得到阶梯矩阵$U$或最简矩阵$R$时，我们能够找出与$A$相关子空间的一个基，那么我们不得不看一下满秩的情况：

当秩尽可能大的时候，$r=n\ or\ r=m\ or\ r=m=n$，矩阵存在左逆$B$或右逆$C$或逆$A^{-1}$。

接下来我们轮流讨论四个子空间，他们里面有两个是相似的，另两个是新的。

1. $A$的列空间用$C(A)$表示，它的维数是秩$r$。
2. $A$的零空间用$N(A)$表示，它的维数是$n-r$。
3. $A$的行空间是$A^{T}$的列空间，即$C(A^{T})$，它有$A$的行生成，维数也是$r$。
4. $A$的左零空间是$A^{T}$的零空间，它包含使$A^{T}y=0$的所有向量$y$，写作$N(A^{T})$，它的维数是_

最后两个子空间来自于$A^{T}$，如果$A$是一个$m\times n$ 的矩阵，那么我们将看到主空间包含了四个子空间：

零空间$N(A)$和行空间$C(A^{T})$是$R^{n}$的子空间，左零空间$N(A^{T})$和列空间$C(A)$是$R^{m}$的子空间。

行有$n$个元素，列有$m$个元素，对于一个简单的矩阵如

$$A=U=R=\begin{bmatrix} 1&0&0\\0&0&0 \end{bmatrix}$$

列空间是通过第一列的直线，行空间是通过$\begin{bmatrix}1&0&0\end{bmatrix}^{T}$的直线，它位于$R^3$里，零空间是$R^3$中的一个平面，左零空间是$R^2$里的一条线：

$$N(A)\text{包含} \begin{bmatrix} 0&1&0 \end{bmatrix} \text{和} \begin{bmatrix} 0&0&1 \end{bmatrix}, \qquad N(A^{T})\text{包含} \begin{bmatrix} 0&1 \end{bmatrix}$$

注意所有向量是列向量，甚至行都是转置的，$A$的行空间是$A^{T}$的列空间，我们的问题是将$U$的四个空间和$A$的四个空间联系起来：

$$U=\begin{bmatrix} 1&3&3&2\\0&0&3&3\\0&0&0&0 \end{bmatrix} \text{来自} A=\begin{bmatrix} 1&3&3&2\\2&6&9&7\\-1&-3&3&4 \end{bmatrix}$$

为了新鲜感，我们以一个有趣的顺序介绍这四个子空间。

3.$A$的行空间，对于像$U$这样的阶梯矩阵，行很明显，它包含行的所有组合，但是第三行没做什么贡献，前两行是行空间的一个基。同样的规则应用到每个阶梯矩阵$U\ or\ R$，他们有$r$个主元和$r$个非零行：非零行是一个基，行空间维数是$r$。这使得我们很容易处理原始矩阵$A$。

13、$A$的行空间和$U$的行空间有相同的维数$r$并且基也相同，因为$A$ 的行空间和$U(R)$行空间一样。

原因是每个初等变换没有改变行空间，$U$中的行是$A$中行的组合，因此$U$的行空间不包含新的东西。同时，因为每步是可逆的，所以也没有丢失；$A$的行可以从$U$中恢复。$A,U$ 有不同的行，但是行的组合是相同的：相同的空间！

注意我们开始没有说$A$的$m$行生成空间，舍弃掉$m-r$行得到一个基，根据12，我们可以这么做的，但是决定留哪些行和舍弃哪些行可能会比较困难，所以更容易的做法是取$U$的非零行。

2.$A$的零空间，消元在不改变解的情况下简化了线性方程组，$Ax=0$化简为$Ux=0$，并且这个过程是可逆的。$A$的零空间和$U,R$的零空间是一样的，$Ax=0$中只要$r$个解是无关的，选择$Ax=0$的$n-r$解可以给出零空间的一个基：

14、零空间$N(A)$维数是$n-r$，特解是一个基——每个自由变量给定值1，而其他自由变量设为0，那么$Ax=0,Ux=0,Rx=0$通过回代得出主元变量。

这就是求$Ux=0$的准确方法，上面的例子中主元在1,3列，因此自由变量是2,4列的$v,y$，零空间的基是

$$\begin{matrix} v&=&1\\y&=&0 \end{matrix} \quad x_1= \begin{bmatrix} -3\\1\\0\\0 \end{bmatrix} ;\quad \begin{matrix} v&=&0\\y&=&1 \end{matrix} \quad x_2= \begin{bmatrix} 1\\0\\-1\\0 \end{bmatrix}$$

任何组合$c_1x_1+c_2x_2$都会有$v,y$元素，所以$c_1x_1+c_2x_2=0$的唯一方式是$c_1=c_2=0$，所以这些向量是无关的，他们也产生零空间；完整解是$vx_1+yx_2$，因此$n-r=4-2=2$个向量是一个基。

零空间也叫作$A$的核，它的维数$n-r$叫做零度。

1.$A$的列空间，列空间有时叫做值域。这和一般意义上的值域意义是一致的，就是所有可能值$f(x)$的集合；$x$在定义域内而$f(x)$在值域内，对于我们的情况函数是$f(x)=Ax$，它的定义域包含$R^n$中的所有$x$；他的值域是所有可能的向量$Ax$，也就是列空间。(在一些书中我们叫它$R(A)$)

我们的问题是找出$U,A$列空间的基，这些空间是不同的，但是他们维数是一样的。

$U$的第一和第三列是列空间的一个基，他们是含有主元的列，其他列都是这两列的一个组合。更进一步，原始矩阵$A$ 同样如此——虽然他们列不相同。$A$的主元列是它列空间的一个基，第二列是第一列的三倍和$U$一样，第四列等于列3-列1，相同的列空间告知了我们这些相关性。

理由是这样的：当$Ux=0$时$Ax=0$，两个系统是等价的并有相同的解，$U$的第四列也是列3-列1，$A$列的线性相关性和$U$ 列的是互相匹配的，并且有相同的系数。如果$A$的集合是无关的，那么对应$U$的列也是无关的，反之亦然。

为了找出列空间$C(A)$的一个基，我们利用$U$，$r$个包含主元的列作为$U$列空间的一个基，然后我们在$A$中选择同样的$r$列：

15、列空间$C(A)$的维数等于$r$，也等于行空间的维数：无关行的数目等于无关列的数目。$C(A)$的一个基由$A$ 的$r$列组成，他们对应于$U$中含有主元的列。

行空间和列空间有相同的维数$r$！这是线性代数中最重要的定理，简单的说为行的秩等于列的秩。对方阵来说：如果方阵的行是线性无关的，那么它的列同样如此(反之亦然)。

下面举一个例子，考虑$r=3$的情况，阶梯形$U$明显有三个无关行：

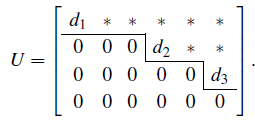
我们说$U$有三个无关列，最多如此。如果我们能说明主元列——1,4,6列——是线性无关的，他们一定是一个基。假设这些主元列的组合得到零：

$$c_1\begin{bmatrix} d_1\\0\\0\\0 \end{bmatrix} + c_2\begin{bmatrix} \ast\\d_2\\0\\0 \end{bmatrix} + c_1\begin{bmatrix} \ast\\ \ast\\d_3\\0 \end{bmatrix}= \begin{bmatrix} 0\\0\\0\\0 \end{bmatrix}$$

从下往上看，$c_3$必须是零，因为$d_3\neq 0$，那么$c_2$ 必须是零，因为$d_2\neq 0$，最终$c_1=0$。因为当且仅当$Ux=0$时$Ax=0$，无论原始矩阵$A$ 是什么，它的1,4,6列是$C(A)$的一个基。

行空间和列空间在$A$上执行消元后变得很清楚，现在我们开始第四个基本子空间，因为前三个子空间是$C(A),N(A),C(A^{T})$，那么第四个空间肯定是$N(A^{T})$，它是$A$转置的零空间或者说是$A$的左零空间，$A^{T}y=0$意味着$y^{T}A=0$，向量出现在$A$的左边。

4.$A$的左零空间(=$A^{T}$的零空间)，如果$A$是$m\times n$矩阵，那么$A^{T}$是$n\times m$矩阵，它的零空间是$R^{m}$的一个子空间；向量$y$有$m$个元素。当写成$y^{T}A=0$时，这些元素乘以$A$的行得到零行：

$$y^{T}A=\begin{bmatrix} y_1&\cdots&y_m \end{bmatrix} \begin{bmatrix} A \end{bmatrix}= \begin{bmatrix} 0&\cdots&0 \end{bmatrix}$$

零空间$N(A^{T})$的维数很容易找到，对于任意矩阵，主元变量的数目加上自由变量的数目肯定是总的列数。对于$A$就是$r+(n-r)=n$，换句话说，秩加上零度等于$n$：

$$C(A)\text{的维数}+N(A)\text{的维数}=\text{列数}$$

这个法则同样可以用到$A^{T}$上，它有$m$列。

16、$N(A^{T})$的零空间维数是$m-r$。

$y^{T}A=0$的$m-r$个解隐藏在消元中，$A$的行组合产生$m-r$个$U$的零行，从$PA=LU\ or\ L^{-1}PA=U$开始，矩阵$L^{-1}P$的最后$m-r$行一定是左零空间的一个基，因为他们乘以$A$得到$U$中的零行。

在我们$3\times 4$的例子力，零行是3-2(行2)+5(行1)，因此$y$的元素为5,-2,3，在右边有同样的组合$b_3-2b_2+5b_1$，这样的话最后的方程是0=0。向量$y$是左零空间的一个基，维数是$m-r=3-2=1$，它是$L^{-1}P$的最后一行，在$U$中得到零行，$A^{T}y=0$肯定有解。

目前为止$N(A^{T})$讲的比较少，我们在下一篇文章中会讲到它在基尔霍夫定律中的物理意义，那时候详细讲效果会更好点。

现在我们知道四个空间的维数，让我们总结一下

1. $C(A)=A$的列空间；维数是$r$。
2. $N(A)=A$的零空间；维数是$n-r$。
3. $C(A^{T})=A$的行空间；维数是$r$。
4. $N(A^{T})=A$的左零空间；维数是$m-r$。

例1：矩阵$A=\begin{bmatrix}1&2\\3&6\end{bmatrix}$行列为2$m=n=2$，秩为1$r=1$。

1. 列空间包含所有$\begin{bmatrix}1\\3\end{bmatrix}$的倍数，第二列和第一列方向相同不产生新的东西。
2. 零空间包含$\begin{bmatrix}-2\\1\end{bmatrix}$ 的所有倍数，这个向量满足$Ax=0$。
3. 行空间包含$\begin{bmatrix}1\\2\end{bmatrix}$的所有倍数，我把它写成列向量，因为严格来讲它是$A^{T}$的列空间。
4. 左零空间包含$\begin{bmatrix}-3\\1\end{bmatrix}$的所有倍数，$A$ 行的系数-3和1相加得到零，所以$A^{T}y=0$。

这个例子中四个空间都是一条直线，这纯属偶然，因为$r=1,n-r=1,m-r=1$。图1中展示了两对线是垂直的，这个可不是偶然！

如果我将$A$的最后一个元素改成7，所有的维数都是不同的，行空间和列空间维数是2，零空间和左零空间只有向量$x=0,y=0$，矩阵是可逆的。

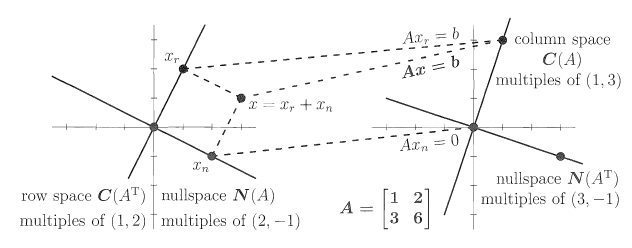
图1

逆的存在性

我们知道如果$A$有左逆($BA=I$)和右逆($AC=I$)，那么这两个逆相等：$B=B(AC)=(BA)C=C$。现在我们从矩阵的秩开始探讨什么矩阵存在逆，简单地说就是只有当矩阵的秩尽可能大时才会存在逆。

秩肯定满足$r\leq m,r\leq n$，一个$m\times n$矩阵不可能超过$m$个无关行或$n$个无关列，我们想证明当$r=m$时有一个右逆，使得$Ax=b$有解，当$r=n$时，有一个左逆，使得解(如果解存的的话)是唯一的。

只要方阵才能$r=m,r=n$，因此才能即有存在性又有唯一性，只有方阵才能保证两边都有逆。

17、存在：行满秩$r=m$。当且仅当列生成$R^m$时，$Ax=b$对每个$b$至少有一个解$x$，所以$A$有一个右逆$C$ 使得$AC=I_m$，这只有在$m\leq n$时才可能。

唯一：列满秩$r=n$。当且仅当列是线性无关的时候，$Ax=b$对每个$b$最多有一个解$x$，所以$A$有一个左逆$B$ 使得$BA=I_n$，这只有在$m\geq n$时才可能。

在存在的情况中，一个可能解是$x=Cb$，因为$Ax=ACb=b$，但是如果其他右逆的话将会有其他解，当列生成$R^m$时解的个数为1或$\infty$。

在唯一的情况中，如果$Ax=b$有一个解，那么它肯定是$x=BAx=Bb$，但是不可能有其他解，解的个数是0或1。

如果逆存在的话，他们最简单的形式如下：

$$B=(A^{T}A)^{-1}A^{T}\quad and \quad C=A^{T}(AA^{T})^{-1}$$

确定的是$BA=I,AC=I$，但是不确定的事$A^TA,AA^T$是否可逆，我会在之后的文章中证明$A^TA$在秩为$n$时是可逆的，$AA^T$在秩为$m$时是可逆的，总之秩尽可能大才会存在逆。

例2：考虑一个秩为2的$2\times 3$ 矩阵：

$$A=\begin{bmatrix} 4&0&0\\0&5&0 \end{bmatrix}$$

因为$r=m=2$，定理保证存在右逆$C$：

$$AC=\begin{bmatrix} 4&0&0\\0&5&0 \end{bmatrix} \begin{bmatrix} \frac{1}{4}&0\\0&\frac{1}{5}\\c_{31}&c_{32} \end{bmatrix}= \begin{bmatrix} 1&0\\0&1 \end{bmatrix}$$

存在很多右逆，因为$C$的最后一行可任意赋值，只是存在但不唯一的情况。就好着呢$A$没有左逆，因为$BA$肯定包含零，特殊的右逆$C=A^T(AA^T)^{-1}$将$c_{31},c_{32}$选为零：

$$A^T(AA^T)^{-1}= \begin{bmatrix} 4&0\\0&5\\0&0 \end{bmatrix} \begin{bmatrix} \frac{1}{16}&0\\0&\frac{1}{25} \end{bmatrix}= \begin{bmatrix} \frac{1}{4}&0\\0&\frac{1}{5}\\0&0 \end{bmatrix} =C$$

这是一个伪逆——我会在后面的文章详细介绍，$A$的转置有无限多个左逆：

$$BA^T=\begin{bmatrix} \frac{1}{4}&0&b_{13}\\0&\frac{1}{5}&b_{23} \end{bmatrix} \begin{bmatrix} 4&0\\0&5\\0&0 \end{bmatrix} =\begin{bmatrix} 1&0\\0&1 \end{bmatrix}$$

现在$B$的最后一列可任意赋值，最好的左逆(也叫做伪逆)是$b_{13}=b_{23}=0$。当$r=n$时这就是唯一的情况，因为$n-r=0$，所以没有自由变量，如果有解的话那也只有一个：

$$\begin{bmatrix} 4&0\\0&5\\0&0 \end{bmatrix} \begin{bmatrix} x_1\\x_2 \end{bmatrix}= \begin{bmatrix} b_1\\b_2\\b_3 \end{bmatrix} \text{在$b_3=0$时才有解}$$

长方形矩阵不可能既满足存在性又满足唯一性，如果$m$与$n$ 不同，那么不可能$r=m,r=n$。

方阵正好相反，如果$m=n$，那么它存在左逆的话肯定存在右逆，只可能有一个逆，即$B=C=A^{-1}$。当矩阵是方阵时，存在性暗示着唯一性而唯一性也暗示着存在性。可逆的条件就是满秩：$r=m=n$：

1. 列生成$R^n$，所以$Ax=b$对每个$b$至少有一个解。
2. 列是独立的，所以$Ax=0$只有一个解$x=0$。
3. $A$的行生成$R^n$。
4. 行是线性无关的。
5. 可以完整的进行消元：$PA=LDU$，有$n$个主元。
6. $A$的行列式不等于零。
7. 零不是$A$的特征值。
8. $A^TA$是正定的

中间的一些概念后面会陆续给出，这里是为了说明这些条件互相都是等价的，他们都确保$A$是可逆的。

这里有一个典型的应用，对于$n-1$次的多项式$P(t)$，给定任意值$b_1,\ldots,b_n$，存在$n-1$次的多项式满足这些值：$P(t_i)=b_i$，这就是我们要处理的方阵；$P(t)=x_1+x_2t+\cdots+x_nt^{n-1}$里系数的个数$n$和方程个数相等：

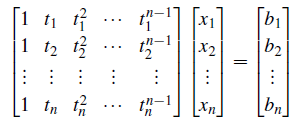
这个范德蒙矩阵是$n\times n$的且满秩，$Ax=b$肯定有解(一个多项式肯定可以在不同的点$t_i$处通过$b_i$)，随后我们还会求$A$ 的行列式，它不等于零。

秩为1的矩阵

最后考虑最容易的情况，也就是秩尽可能小(除了零矩阵，它的秩为0)。数学的一个基本主题是给定一个复杂的东西，如果将它变成一些简单的部分。对于线性代数来说，最简单的部分就是秩为1的矩阵：

$$A=\begin{bmatrix} 2&1&1\\4&2&2\\8&4&4\\-2&-1&-1 \end{bmatrix}$$

每一行都是第一行的倍数，所以行空间是一维的。事实上，我们可以将矩阵写成一个列向量和一个行向量的乘积：

$$\begin{bmatrix} 2&1&1\\4&2&2\\8&4&4\\-2&-1&-1 \end{bmatrix}= \begin{bmatrix} 1\\2\\4\\-1 \end{bmatrix} \begin{bmatrix} 2&1&1 \end{bmatrix}$$

一个$4\times 1$矩阵和$1\times 3$矩阵相乘得到$4\times 3$矩阵，这个结果秩为1，同样的，列是同一列向量的倍数，列空间维数同样是$r=1$，简化为一条线。

每个秩为1的矩阵都可以写成简化的形式$A=uv^{T}$。行是向量$v^T$的倍数，列是向量 u <script type="math/tex" id="MathJax-Element-26549">u</script>的倍数，行空间和列空间是一条直线——这就是最简单的情况。