漫步线性代数二十——快速傅里叶变换（下）

快速傅里叶变换

傅里叶分析是一个很美妙的理论，而且它还很实用。在频域分析波形可以很好的将信号分离开来，相反的过程又能回到时域中。处于物理和数学的缘故，指定实用指数函数，我们感觉最主要的原因就是：如果我们对$e^{ikx}$求导、积分或将$x$变成$x+h$，结果依然是$e^{ikx}$的倍数，指数函数非常适用于微分方程，积分方程和差分方程，每个频域分量有自己的运作方式，就像特征值一样，然后阿门重新组合得到问题的解。信号的分析和合成(从$y$中计算$c$，从$c$中计算$y$)是科学计算的中心问题。

我们想要展示$Fc,F^{-1}y$计算非常快，关键点就是$F_4$到$F_2$的关系：

$$F_4= \begin{bmatrix} 1&1&1&1\\ 1&i&i^2&i^3\\ 1&i^2&i^4&i^6\\ 1&i^3&i^8&i^9 \end{bmatrix} \text{接近} F_2^{*}= \begin{bmatrix} 1&1&&\\ 1&-1&&\\ &&1&1\\ &&1&-1 \end{bmatrix}$$

$F_4$包含$w_4=i$，1的四次根，$F_2^{*}$包含$w_2=-1$，1的平方根。注意$F_2^*$有一半的元素都是零，做两次$2\times 2$的变换仅需要直接进行$4\times 4$变换时间的一半，如果$64\times 64$变化可以用两个$32\times 32$变换替换，那么运行时间将减少一般。之所有能够如此，原因在于$w_{64}$ 和$w_{32}$之间存在一个简单的联系：

$$(w_{64})^2=w_{32},\quad\text{或者}(e^{2\pi i/64})^2=e^{2\pi i/32}$$

从圆上的点看，32次根是64次根的两倍，如果$w^{64}=1$，那么$(w^2)^{32}=1$，如果$m$是$n$的一半，那么$m$次根是$n$ 次根的平方：

$$\begin{equation} \text{如果} m=\frac{1}{2}n,\text{那么}w_n^2=w_m\tag1 \end{equation}$$

$FFT$的速度取决于像$2^{10}=1024$这样的合数。如果没有快速变换，那么$F$ 乘以$c$就需要$(1024)^2$次乘法，相比之下，快速变换只需要$5\cdot 1024$ 步，整整快了200倍。一般来讲，当$n=2^{\ell}$时，我们用$\frac{1}{2}n\ell$代替$n^2$，我们先将$F_n$和两个$F_{n/2}$联系起来，然后在和四个$F_{n/4}$ 联系起来，如此不断进行下去最后可以得出很小的$F$，通常来讲$n^2$步会减到$\frac{1}{2}n\log_2^n$。

我们现在看看$y=F_nc$(一个有$n$个元素的向量)如何从两个只有一半长度的向量中恢复回来。第一步是将$c$分成奇数和偶数两部分：

$$c'=(c_0,c_2,\ldots,c_{n-2})\quad c''=(c_1,c_3,\ldots,c_{n-1})$$

利用这两个向量，我们变换$y'=F_mc',y''=F_mc''$，这两个乘法的矩阵$F_m$比原来要小。现在问题变成如何从$y',y''$ 中恢复$y$，Cooley和Tukey注意到了如何求解这个问题：

33、向量$y=F_nc$的前$m$项和后$m$项是

$$\begin{equation} \begin{array}{rl} y_j=y_j'+w_n^jy_j'',&\quad j=0,\ldots,m-1 \\ y_{j+m}=y_j'-w_n^jy_j'',&\quad j=0,\ldots,m-1 \end{array}\tag2 \end{equation}$$

因此第三步就是：将$c$分成$c',c''$，用$F_m$将他们变成$y',y''$并且利用$(13)$进行重构。

这种不断分半的想法可以一直重复进行，例如从$F_{1024}$到$F_{512}$再到$F_{256}$，如果我们从$n=2^{\ell}$开始到一直到$n=1$，那么最终的计数是$\frac{1}{2}n\ell$。另一种计算方法是：从$n=2^{\ell}$到$n=1$需要$\ell$ 步，每一步需要$n/2$次乘法，相当于是$F_n$的一个分解：

$$\begin{equation} F_{1024}=\begin{bmatrix} I_{512}&D_{512}\\ I_{512}&-D_{512} \end{bmatrix} \begin{bmatrix} F_{512}&\\ &F_{512} \end{bmatrix} \begin{bmatrix} \text{奇偶置换矩阵} \end{bmatrix}\tag3 \end{equation}$$

所需的代价近似是线性的，傅里叶分析完全可以用FFT进行转换，为了证实方程(13)，我们将$y_i$分成奇数项和偶数项：

$$y_i=\sum_{k=0}^{n-1}w_n^{jk}c_k\text{等价于}\sum_{k=0}^{m-1}w_n^{2jk}c_{2k}+\sum_{k=0}^{m-1}w_n^{(2k+1)j}c_{(2k+1)}$$

右边的两个和式分别有$m=\frac{1}{2}n$项。因为$w_n^2=w_m$，所以这两个和式子可以表示为：

$$\begin{equation} y_j=\sum_{k=0}^{m-1}w_m^{jk}c_k^{'}+w_n^j\sum_{k=0}^{m-1}w_m^{jk}c_k^{''}=y_j^{'}+w_n^jy_j^{''}\tag4 \end{equation}$$

在方程(13)的第二部分，$j+m$部分有一个符号的变化：

在和式里面，因为$w_m^{km}=1^k=1$，所以$w_m^{k(j+1)}$依然为$w_m^{kj}$；在外面，因为$w_n^m=e^{2\pi im/n}=e^{\pi i}=-1$，所以$w_n^{j+m}=-w_n^j$。

FFT的想法用其他的素数$n$代替后就得到一个新版本，如果$n$本身是一个素数，那么将会有一个全新的算法。

例1:从$n=4$到$n=2$为

$$\begin{bmatrix} c_0\\c_1\\c_2\\c_3 \end{bmatrix} \to \begin{bmatrix} c_0\\c_2\\c_1\\c_3 \end{bmatrix} \to \begin{bmatrix} F_2c'\\F_2c'' \end{bmatrix} \to \begin{bmatrix} y \end{bmatrix}$$

因为每步都是线性的，所以从一个矩阵开始，这些矩阵的乘积也必须是$F_4$：

$$\begin{equation} \begin{bmatrix} 1&1&1&1\\ 1&i&i^2&i^3\\ 1&i^2&i^4&i^6\\ 1&i^3&i^6&i^9 \end{bmatrix}= \begin{bmatrix} 1&&1&\\ &1&&i\\ 1&&-1&\\ &1&&-i \end{bmatrix} \begin{bmatrix} 1&1&&\\ 1&-1&&\\ &&1&1\\ &&1&-1 \end{bmatrix} \begin{bmatrix} 1&&&\\ &&1&\\ &1&&\\ &&&1 \end{bmatrix}\tag5 \end{equation}$$

我们可以看出中间的是两个$F_2$，右边是将$c$分成$c^{'},c^{''}$的置换矩阵，左边是用乘以$w_n^j$的矩阵。如果我们从$F_8$开始，那么中间的矩阵就是两个$F_4$，所以FFT相当于傅里叶矩阵的因式分解！$n^2$个非零向量矩阵$F$近似为$\ell=\log_2^n$个矩阵(他们有$n\ell$个非零元素)相乘的结果。

FFT

FFT的第一步是将$F_n$的乘法变成两个$F_m$的乘法，偶数项$(c_0,c_2)$从奇数项$(c_1,c_3)$中分离出来，如1给出了$n=4$时的流图(flow graph)。对于$n=8$，只要用$F_2$代替$F_4$ 即可。新元素$w_4=i$是老元素$w=w_8=e^{2\pi i/8}$ 的平方，流图给出了$c$进入FFT的顺序。

每一步需要$\frac{1}{2}n$次乘法，所以最终需要$\frac{1}{2}n\log^n$。

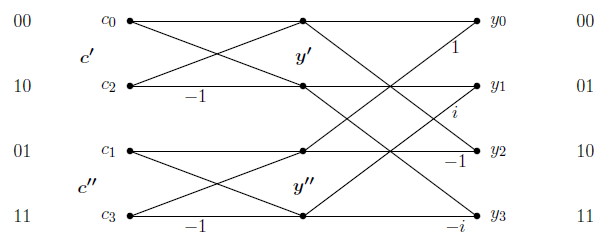
图2