漫步线性代数二十四——行列式应用_线性代数行列式的应用-CSDN博客

本文探讨了线性代数中的四大核心计算问题：计算矩阵的逆、求解线性方程组Ax=b、计算盒子体积以及主元公式。通过具体实例和公式推导，详细介绍了伴随矩阵在矩阵逆中的应用、克拉姆法则求解线性方程组、行列式与几何体积的关系以及主元公式的消元法等关键概念。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

本篇文章介绍四个应用： $A$ 的逆，求解 $Ax=b$ ，盒子的体积以及主元。他们都是线性代数里面非常关键的计算，而行列式给出了这些答案的公式。

1、计算 $A^{-1}$ 。 $2\times 2$ 矩阵展示了伴随矩阵如何表示 $A^{-1}$ ：

[a c b d] - 1 = 1 a d - b c [d - c - b a]

$\begin{bmatrix} a&b\\ c&d \end{bmatrix}^{-1}= \frac{1}{ad-bc} \begin{bmatrix} d&-b\\ -c&a \end{bmatrix}$

伴随矩阵还需乘以行列式，当 $\det A$ 非零时， $A$ 是可逆的。 $C_{11}=d$ 是 $a$ 的代数余子式， $C_{12}=-c$ 是 $b$ 的代数余子式(注意负号)，而 $C_{12}$ 放在了第二行第一列！

$a,b$ 分别和 $C_{11},C_{12}$ 相乘得到 $ad-bc$ ，这是 $\det A$ 的代数余子式展开式，也是我们需要的线索： $A^{-1}$ 就是用伴随矩阵除以 $\det A$

A - 1 = C T det A (A - 1) i j = C i j det A (1)

$\begin{equation} A^{-1}=\frac{C^T}{\det A}\quad (A^{-1})_{ij}=\frac{C_{ij}}{\det A}\tag1 \end{equation}$

我们的目标是验证这个公式，另外由此我们还看出为何 $AC^T=(\det A)I$ ：

⎡ ⎣ ⎢ ⎢ a 11 ⋮ a n 1 \dots \dots a 1 n ⋮ a n n ⎤ ⎦ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ C 11 ⋮ C 1 n \dots \dots C n 1 ⋮ C n n ⎤ ⎦ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ det A ⋮ \dots \dots 0 ⋮ det A ⎤ ⎦ ⎥ ⎥ (2)

$\begin{equation} \begin{bmatrix} a_{11}&\cdots&a_{1n}\\ \vdots&&\vdots\\ a_{n1}&\cdots&a_{nn} \end{bmatrix} \begin{bmatrix} C_{11}&\cdots&C_{n1}\\ \vdots&&\vdots\\ C_{1n}&\cdots&C_{nn} \end{bmatrix}= \begin{bmatrix} \det A&\cdots&0\\ \vdots&&\vdots\\ &\cdots&\det A \end{bmatrix}\tag2 \end{equation}$

第一列 $C_{11},\ldots,C_{1n}$ 乘以 $a_{11},\ldots,a_{1n}$ 得到对角元素 $\det A$ ， $A$ 的每一行乘以它的代数余子式都得到 $\det A$ 。

那么关键问题是：为什么对角线外的元素都是零呢？如果我们将第一行的元素 $a_{1j}$ 和第二行的代数余子式 $C_{2j}$ 进行组合，为什么结果是零呢？

a 11 C 21 + a 12 C 22 + \dots + a 1 n C 2 n = 0 (3)

$\begin{equation} a_{11}C_{21}+a_{12}C_{22}+\cdots+a_{1n}C_{2n}=0\tag3 \end{equation}$

答案就是：我们在计算一个新矩阵 $B$ 的行列式。 $A$ 的第一行复制到第二行得到矩阵 $B$ ，那么矩阵 $B$ 就有相同的两行， $\det B=0$ 。方程(3)是沿着第二行得到 $\det B$ 展开式，其中 $B$ 和矩阵 $A$ 有相同的代数余子式(因为在求解代数余子式时需丢掉第二行)，这个非凡的矩阵乘法(2)是完全正确的。

乘法 $AC^T=(\det A)I$ 直接得出 $A^{-1}$ ，记住去掉矩阵 $A$ 第 $i$ 行第 $j$ 列的代数余子式放到 $C^T$ 的第 $j$ 行第 $i$ 列，然后除以 $\det A$ (不能等于0)就得到 $A^{-1}=C^T/\det A$ 。

例1：和矩阵的逆是微分矩阵：

A = ⎡ ⎣ ⎢ 100110111 ⎤ ⎦ ⎥ 的 逆 为 A - 1 = C T det A = ⎡ ⎣ ⎢ 100 - 1 10 0 - 1 1 ⎤ ⎦ ⎥

$A= \begin{bmatrix} 1&1&1\\ 0&1&1\\ 0&0&1 \end{bmatrix} \text{的逆为} A^{-1}=\frac{C^T}{\det A}= \begin{bmatrix} 1&-1&0\\ 0&1&-1\\ 0&0&1 \end{bmatrix}$

因为代数余子式包含 $(-1)^{i+j}$ ，所以会有符号。

2、求解 $Ax=b$ 。 $x=A^{-1}b$ 仅仅就是 $C^Tb$ 除以 $\det A$ ，这里介绍一个非常出名的求 $(x_1,\ldots,x_n)$ 的方法:

克拉姆法则： $x=A^{-1}b$ 的第 $j$ 个元素是比值

x j = det B j det A, 其 中 B j = ⎡ ⎣ ⎢ ⎢ a 11 ⋮ a n 1 a 12 ⋮ a n 2 b 1 ⋮ b n a 1 n ⋮ a n n ⎤ ⎦ ⎥ ⎥

$x_j=\frac{\det B_j}{\det A},\text{其中}\ B_j= \begin{bmatrix} a_{11}&a_{12}&b_{1}&a_{1n}\\ \vdots&\vdots&\vdots&\vdots\\ a_{n1}&a_{n2}&b_{n}&a_{nn} \end{bmatrix}$

证明：对 $\det B$ 按第 $j$ 列展开成代数余子式的形式，因为代数余子式不考虑该列，所以 $\det B_j$ 是 $C^Tb$ 的第 $j$ 个元素：

det B j = b 1 C 1 j + b 2 C 2 j + \dots + b n C n j

$\det B_j=b_1C_{1j}+b_2C_{2j}+\cdots+b_nC_{nj}$

然后用它除以 $\det A$ 就得到 $x_j$ ， $x$ 的每个元素都是两个行列式的比值。

例2：下面方程组

x 1 + 3 x 2 = 0

$x_1+3x_2=0$

2 x 2 + 4 x 2 = 0

$2x_2+4x_2=0$

的解 $x_1$ 需要将第一列换成0,6， $x_2$ 需要将第二列换成0,6：

x 1 = ∣ ∣ ∣ 0 6 3 4 ∣ ∣ ∣ ∣ ∣ ∣ 1 2 3 4 ∣ ∣ ∣ = - 18 - 2 = 9, x 2 = ∣ ∣ ∣ 1 2 0 6 ∣ ∣ ∣ ∣ ∣ ∣ 1 2 3 4 ∣ ∣ ∣ = 6 - 2 = - 3,

$x_1=\frac{\begin{vmatrix}0&3\\6&4\end{vmatrix}}{\begin{vmatrix}1&3\\2&4\end{vmatrix}}=\frac{-18}{-2}=9,\quad x_2=\frac{\begin{vmatrix}1&0\\2&6\end{vmatrix}}{\begin{vmatrix}1&3\\2&4\end{vmatrix}}=\frac{6}{-2}=-3,\quad$

分母总是 $\det A$ ，如果有1000个方程，那么根据克莱姆法则，需要1001个行列式。

3、盒子的体积。当所有角都是直角——此时边互相垂直，行列式和体积的联系就非常紧密，此时的盒子的形状是矩形的，从而体积就是边长的乘积： $volumn=\ell_1\ell_2\cdots\ell_n$ 。

当盒子的边长是 $A$ 的行时，我们想从 $\det A$ 中得到同样的 $\ell_1\ell_2\cdots\ell_n$ 。在直角的情况下，这些行是正交的， $AA^T$ 是对角矩阵：

A A T = ⎡ ⎣ ⎢ ⎢ r o w 1 ⋮ r o w n ⎤ ⎦ ⎥ ⎥ ⎡ ⎣ ⎢ ⎢ ⎢ r o w 1 \dots r o w n ⎤ ⎦ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ℓ 21 0 ⋱ 0 ℓ 2 n ⎤ ⎦ ⎥ ⎥ ⎥

$AA^T=\begin{bmatrix} row\ 1\\ \vdots\\ row\ n \end{bmatrix} \begin{bmatrix} r&&r\\ o&&o\\ w&\cdots&w\\ 1&&n \end{bmatrix} =\begin{bmatrix} \ell_1^2&&0\\ &\ddots&\\ 0&&\ell_n^2 \end{bmatrix}$

$\ell_i$ 是行(边)的长度，因为行是正交的，所以对角线外的元素都是零。利用乘法和转置法则：

ℓ 21 ℓ 22 \dots ℓ 2 n = det (A A T) = (det A) (det A T) = (det A) 2

$\ell_1^2\ell_2^2\cdots\ell_n^2=\det(AA^T)=(\det A)(\det A^T)=(\det A)^2$

这个方程的平方根说明了行列式等于体积。而 $\det A$ 的符号暗示了是使用右手坐标(也就是通常的 $x-y-z$ )，还是左手坐标(像 $y-x-z$ )。

如果角度不是 $90^{\circ}$ ，那么体积就不是长度的乘积。在平面上(如图1)，平行四边形的“体积”等于底边 $\ell$ 乘以高 $h$ ，向量 $b-p$ 就是第二行 $b=(a_{21},a_{22})$ 减去它在第一行上的投影 $p$ ，关键点是：根据5，用第一行的倍数减去第二行时 $\det A$ 不变，我们可以将平行四边形变成一个矩形。

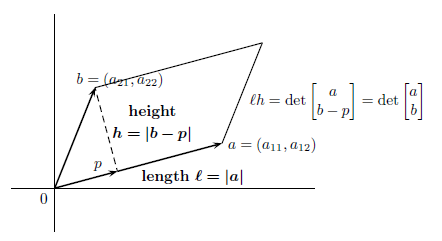
图1

对于 $n$ 维的情况，将盒子变成矩形需要很长时间，但是思路就是如此，如果我们从每行减去它在前面行所生成空间的投影，体积和行列式都不变，通过格拉姆-施密特过程产生正交的行，这时体积=行列式，所以对于开始的行这个等式同样成立。

现在我们介绍完了体积和行列式之间的关系，但是很有必要回过头来看看最简单的情况，我们知道

det [1001] = 1, det [1 c 01] = 1

$\det \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}=1,\quad \det \begin{bmatrix} 1&0\\ c&1 \end{bmatrix} =1$

这些行列式给出了体积——或者面积(因为这是在二维空间)，如图2所示，平行四边形底和高都是1，所以面积也是1。

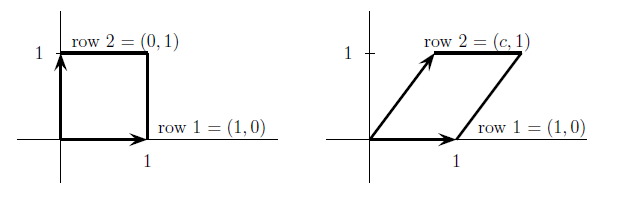
图2

4、主元公式。最后我们讨论一下消元，此时考虑不需要行交换的情况。观察的要点是第 $k$ 个主元完全由 $A$ 的左上角子矩阵 $A_k$ 确定， $A$ 的其余行和列对它没有影响：

A = ⎡ ⎣ ⎢ a c g b d h e f i ⎤ ⎦ ⎥ \to ⎡ ⎣ ⎢ a 0 g b (a d - b c) / a h e (a f - e c) / a i ⎤ ⎦ ⎥

$A=\begin{bmatrix} a&b&e\\ c&d&f\\ g&h&i \end{bmatrix} \to \begin{bmatrix} a&b&e\\ 0&(ad-bc)/a&(af-ec)/a\\ g&h&i \end{bmatrix}$

第一个主元只取决于第一行和第一列，第二个主元 $(ad-bc)/a$ 值取决于 $2\times 2$ 的子矩阵 $A_2$ ， $A$ 的其余部分不会影响到它。实际上，不仅仅是主元，整个左上角矩阵的 $L,D,U$ 都只取决于 $A$ 的左上角：

A = L D U = ⎡ ⎣ ⎢ 1 c / a * 1 * 1 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ a (a d - b c) / a * ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ 1 b / a 1 * * 1 ⎤ ⎦ ⎥

$A=LDU= \begin{bmatrix} 1&&\\ c/a&1&\\ *&*&1 \end{bmatrix} \begin{bmatrix} a&&\\ &(ad-bc)/a&\\ &&* \end{bmatrix} \begin{bmatrix} 1&b/a&*\\ &1&*\\ &&1 \end{bmatrix}$

从上例我们看出，前两行和两列就是子矩阵 $A_2$ 的分解，如果没有行交换的前提下，这条规则恒成立。

4、如果 $A$ 分解为 $LDU$ ，那么左上角满足 $A_k=L_kD_kU_k$ 。

证明的关键在于进行其他行的消元之前，先将左上角的确定下来，或者使用块乘法规则：

L D U = [L k B 0 C] [D k 0 0 E] [U k 0 F G] = [L k D k U k B D k U k L k D k F B D k F + C E G]

$LDU= \begin{bmatrix} L_k&0\\ B&C \end{bmatrix} \begin{bmatrix} D_k&0\\ 0&E \end{bmatrix} \begin{bmatrix} U_k&F\\ 0&G \end{bmatrix}= \begin{bmatrix} L_kD_kU_k&L_kD_kF\\ BD_kU_k&BD_kF+CEG \end{bmatrix}$

将最后的矩阵和 $A$ 进行比较，我们发现 $L_kD_kU_k$ 和 $A_k$ 是一致的，那么：

det A k = det L k det D k det U k = det D k = d 1 d 2 \dots d k

$\det A_k=\det L_k\det D_k\det U_k=\det D_k=d_1d_2\cdots d_k$

前 $k$ 个主元的乘积是 $A_k$ 的行列式，这和我们已知的整个矩阵的规则一致。因为 $A_{k-1}$ 的行列式由 $d_1d_2\cdots d_{k-1}$ 给出，所以我们用行列式比值的方式分离每个主元 $d_k$ ：

det A k det A k - 1 = d 1 d 2 \dots d k d 1 d 2 \dots d k - 1 = d k (4)

$\begin{equation} \frac{\det A_k}{\det A_{k-1}}=\frac{d_1d_2\cdots d_{k}}{d_1d_2\cdots d_{k-1}}=d_k\tag4 \end{equation}$

对于上面的例子，第二个主元就是比值 $(ad-bc)/a$ ，也就是 $A_2$ 的行列式除以 $A_1$ 的行列式(约定 $A_0=1$ ，这样的话第一个主元就是 $a/1=a$ )。将所有主元相乘就回到我们的行列式：

d 1 d 2 \dots d n = det A 1 det A 0 det A 2 det A 1 \dots det A n det A n - 1 = det A n det A 0 = det A

$d_1d_2\cdots d_{n}=\frac{\det A_1}{\det A_{0}}\frac{\det A_2}{\det A_{1}}\cdots\frac{\det A_n}{\det A_{n-1}}=\frac{\det A_n}{\det A_{0}}=\det A$

根据方程(5)我们可以得出一个结论：当 $\det A_k$ 都不为零时，主元也都不为零。

5、当且仅当子矩阵 $A_1,A_2,\ldots,A_n$ 都是非奇异时，消元法不需要行交换(所以 $P=I,A=LU$ )。

现在考虑一个问题，行交换的次数会一直是奇数或偶数吗？如果是，那么根据2行列式要么为+1，要么为-1。

考虑 $(3,2,1)$ ，我们可以只交换3,1就得到正序列 $(1,2,3)$ ，交换3与2，然后3与1，最后2与1同样得到正序列，对于这两种方式，交换的次数都是奇数，这里得出的论断就是：偶数次的交换不可能从 $(3,2,1)$ 得出正序列。

这里给出它的一个证明。观察置换中的每对数，我们用 $N$ 表示大数在前的对数。这样的话 $N=0$ 表示正序列 $(1,2,3)$ 。而 $(3,2,1)$ 的 $N$ 为3，因为所以数对 $(3,2),(3,1),(2,1)$ 都是大数在前，接下来我们将展示用奇数次变换来改变 $N$ ，直到 $N=0$ 为止。