高斯核函数

线性支持向量机 (Linear-SVM) 被用于线性可分的数据集的二分类问题，当数据集不是线性可分的时候，需要利用到核函数将数据集映射到高维空间。这样数据在高维空间中就线性可分。

高斯核函数（Gaussian kernel），也称径向基 (RBF) 函数，是常用的一种核函数。它可以将有限维数据映射到高维空间，我们来看一下高斯核函数的定义：

k(x,x′)=e−||x−x′||22σ2

k(x, x’) = e^{-\frac{||x - x’||^2}{2\sigma2}}
上述公式涉及到两个向量的欧式距离（2范数）计算，而且，高斯核函数是两个向量欧式距离的单调函数。 σ \sigma 是带宽，控制径向作用范围，换句话说， σ \sigma 控制高斯核函数的局部作用范围。当 x x 和x′x’ 的欧式距离处于某一个区间范围内的时候，假设固定 x′ x’， k(x,x′) k(x, x’) 随x的变化而变化的相当显著。

一维情况

令 x′=0 x’ = 0， k(x,0) k(x, 0) 随x的变化情况如下图所示：

σ=1 \sigma = 1

σ=5 \sigma = 5
我们看到，随着 x x 与x′x’的距离的距离的增大，其高斯核函数值在单调递减。并且， σ \sigma越大，那么高斯核函数的局部影响范围就会越大。

二维情况

σ=1 \sigma=1

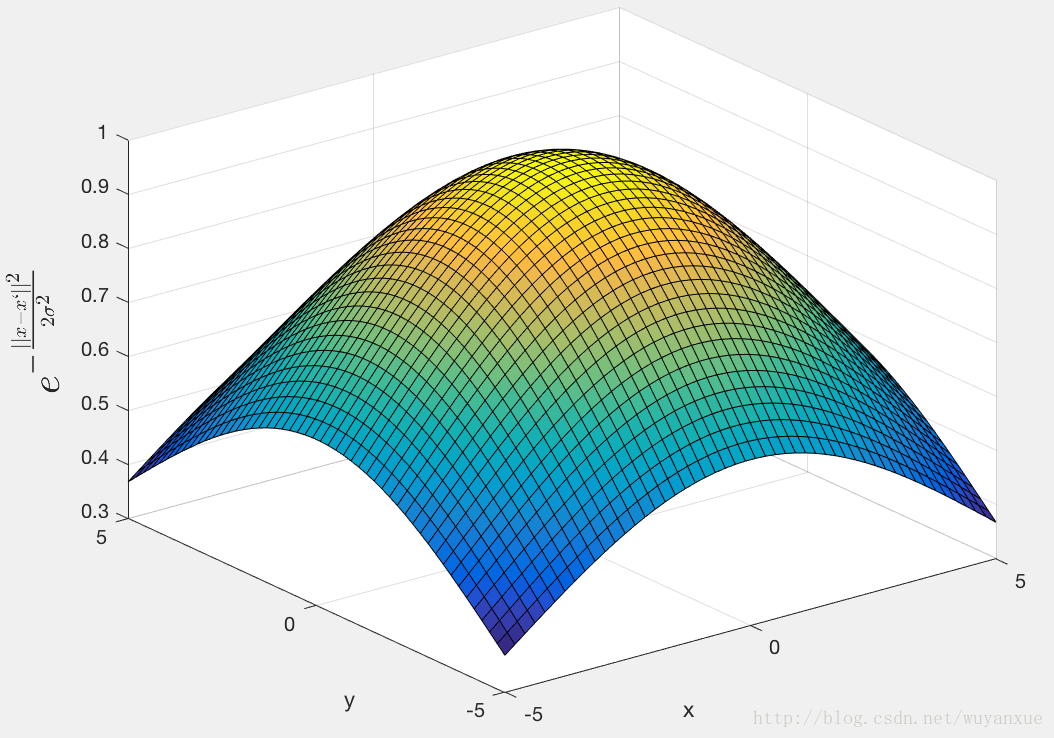
σ=5 \sigma=5

二维可以更加明显的看出高斯核函数局部作用的范围随带通的变化情况。带通越大，高斯核函数的局部影响的范围就越大。在超出这个范围之后，核函数的值几乎不变。

高斯核将数据映射到高维甚至无穷维的原理

通过一些简单的推导，我们可以得到这样的结果，为了描述简单，我们令高斯核中的分母为1.

图片转载自：https://www.zhihu.com/question/46587416?from=profile_question_card
可以看到，高斯核函数通过泰勒展开可以被描述成 ϕ(x)Tϕ(x′) \phi(x)^T\phi(x’)的形式，而 ϕ(x) \phi(x)是无穷维的。

本文转自 https://blog.csdn.net/wuyanxue/article/details/79642758，如有侵权，请联系删除。