最小生成树问题的常规分析过程

这里只是给出按照正常自然人的分析过程，不想涉及代码。
首先理解一下什么是最小生成树，用一个例子
要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。
实际上这个很像背包问题，但是区别在于最小生成树没有重复问题，只要路径最短就可以了。
下面分析一下一个简单的思考过程

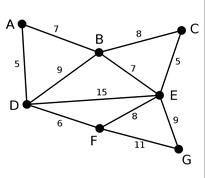
以此图为例子。从A点出发，根据权重，选择D点。此时选择路径AD=5；
然互在和A、D都相关的B、F、E中寻找权重最小的F点；此时选择路径DF=6；
然后在和ADF都相关的点里面再寻找权重最小的点,此时AB的权重最小选择B点。此时选择路径AB=7；
然后在CEF中再寻找权重最小的点。很明显选择E点E点。此时选择路径BE=7；
然后在CG中寻找，很明显选择C点。此时路径为CE=5；
然后再G中寻找，结束：此时路径为EG=9；

上面是自然人的选择过程，的确如此，归纳一下，这个过程是如何完成的，
以一个点为起点，为了最短路径，一定是找权重最小的，寻找到下一个点，然后将找到的点作为一类，再找离这个类最近的点。
然后重复这个过程，直到找完所有点。

接下来需要解决的问题就是，如何用基本数据结构将这种关系（如下）表示出来
A-D 5
A-B 7
。。。

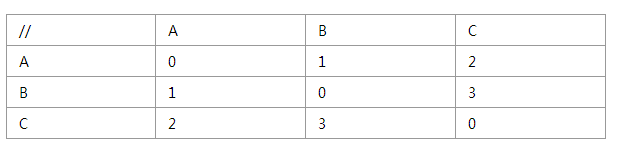
想到用树，但是有个问题就是，在这里ABD是无序的，谁是根节点有点问题。而且要便于后面的查找权重。

用二维数组是可以表示这种关系的，比如