动态系统与控制原理（1）- 系统表达式

_ca_1cm_

已于 2024-06-17 15:52:34 修改

阅读量1.2k

点赞数 1

分类专栏：工程数学文章标签： matlab 算法开发语言

于 2021-02-15 05:07:23 首次发布

本文链接：https://blog.csdn.net/u010720150/article/details/113798725

版权

工程数学专栏收录该内容

4 篇文章 0 订阅

订阅专栏

在上一篇博文中，我提到了，生活中方方面面都是动态系统，并稍微提了一下现代控制理论里的State-Space Representation。这篇博文将描述在现代控制理论中如何表示动态系统。

既然你选择看这篇博文，你对于以下这张图肯定不陌生：

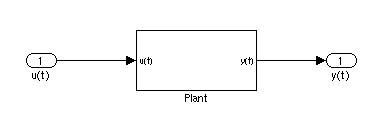
对于系统（plant），变量 $u(t)$ 是输入， $y(t)$ 是输出，可以代表系统的全部动态信息或者部分信息。

上一篇博文提到了人口增长的例子：

$\dot{N}=\alpha N$

假设我们每年统计一次，上面的式子可以变为离散表达式（ $T_s$ 是采样时间）：

$\frac{N(k+1) -N(k)}{T_s}= \alpha N(k)$

如果外界有刺激输入，比方说粮荒或者大丰收，那么系统也可以表示为：

$\frac{N(k+1) -N(k)}{T_s}= \alpha N(k)+u(k)$

也即：

$N(k+1)=(\alpha*T_s+1) N(k)+T_s*u(k)$

我们再看一个例子（Mass-Spring-Damper）：

这个系统的数学表达式是（a是加速度，v是速度）：

$ma+bv+ky=u$

如果我们从一个动态的角度来描述这个系统，那么外力u，位置y，速度v（位置的微分， $\dot{y}$ ），加速度a（速度的微分， $\ddot{y}$ ），都在变化：

$m\ddot{y}(t)+b\dot{y}(t)+ky(t) = u(t)$

线性时不变系统的State-Space Representation

对于连续的系统，我们可以表示为：

$\dot{x}(t)=Ax(t)+Bu(t), x(0)=x_0\\$

with

$x\in \mathbb{R}, A\in\mathbb{R}^{n\times n},u\in\mathbb{R}^{m}, B\in\mathbb{R}^{n\times m}$

对于离散的系统：

${x}(t+1)=\tilde{A}x(t)+\tilde{B}u(t), x(0)=x_0\\$

with

$x\in \mathbb{R}, \tilde{A}\in\mathbb{R}^{n\times n},u\in\mathbb{R}^{m}, \tilde{B}\in\mathbb{R}^{n\times m}$

这里，值得注意的是，有时候便于计算，会将连续系统转化为离散系统，那 $A$ 和 $\tilde{A}$ 的关系是：

$\dot{x}(t)=Ax(t)+Bu(t)\\\Rightarrow \frac{x(t+1) - x(t) }{T_s}=Ax(t)+Bu(t)\\\Rightarrow x(t+1)=(T_sA+I)x(t)+T_sBu(t)$

也即，

$\tilde{A} = T_sA-I$ .

回想上一篇博文中稳定性的判断：当 $A$ 的所以特征值的实数部分都是负数时，系统稳定。那么对于 $\tilde{A}$ ，如果需要系统稳定，我们则需要它的所有特征值的模长小于1。如下图所示：

在复数坐标系中特征值，让连续系统稳定的是左半边，意思是实数部分为负数；让离散系统稳定的是单位圆内，意思是模长小于1。

也可根据下面的MATLAB代码来感受它们的一一对应：

%%
clear, close all, clc

n = 10;
CC = jet(n*5);

A = -randi(10,n,n);
eigA = eig(A)
subplot(1,2,1);
hold on
for k=1:n
    plot(real(eigA(k)), imag(eigA(k)),'*','Color',CC(k*5,:),'LineWidth',1.2)
end

ax = 30;
axis([-ax ax -ax ax]);
axh = gca; 
line(get(axh,'XLim'), [0 0], 'Color', 'k', 'LineWidth',1, 'LineStyle', '-');
line([0 0], get(axh,'YLim'), 'Color', 'k', 'LineWidth',1, 'LineStyle', '-');

dt = 0.01;
At = A*dt+eye(n);
eigAt = eig(At)
subplot(1,2,2);
hold on
for k=1:n
    plot(real(eigAt(k)), imag(eigAt(k)),'*','Color',CC(k*5,:),'LineWidth',1.2)
end

viscircles([0,0],1);
ax = 10;
axis([-ax ax -ax ax]);
axh = gca; 
line(get(axh,'XLim'), [0 0], 'Color', 'k', 'LineWidth',1, 'LineStyle', '-');
line([0 0], get(axh,'YLim'), 'Color', 'k', 'LineWidth',1, 'LineStyle', '-');

（对应关系是 $eig(\tilde{A})=e^{eig(A)*T_s}$ ）

从常微分方程到State-Space Representation

常微分方程可以是很多阶的，比方说上面的mass-spring-damper的例子就是二阶的，而State-Space Representation是一阶。那么我们如何把常微分方程改成State-Space Representation呢？先看一个普遍的表达式：

$y^{n}(t)+a_{n-1}y^{n-1}(t)+\cdots +a_1\dot{y}(t)+a_0y(t)=bu(t)$ .

我们可以定义一个空间向量来表示 $y(t)$ 以及它的各阶微分：

$x(t)= \begin{bmatrix} x_1(t)\\ x_2(t)\\ x_3(t)\\ \vdots \\ x_n(t) \end{bmatrix} = \begin{bmatrix} y(t)\\ \dot{y}(t)\\ \ddot{y}(t)\\ \vdots \\ y^{n-1}(t) \end{bmatrix}$

所以，

$\dot{x}(t)= \begin{bmatrix} \dot{y}(t)\\ \ddot{y}(t)\\ \vdots \\ y^{n}(t) \end{bmatrix}= \begin{bmatrix} x_2(t)\\ x_3(t)\\ \vdots \\ \dot{x}_n(t) =y^{n}(t) \end{bmatrix}$

而 $y^{n}(t)$ 可以通过隔离上面的常微分方程得到：

$y^{n}(t)=-a_0y(t)-a_1\dot{y}(t)-\cdots-a_{n-1}y^{n-1}(t)+bu(t)$

所以，

$\dot{x}(t)= \left\{\begin{matrix} \begin{aligned} &x_2(t)\\ &x_3(t)\\ &\vdots\\ &-a_0x_1(t)-a_1x_2(t)-\cdots-a_{n-1}x_n(t)+bu(t) \end{aligned} \end{matrix}\right.$

用矩阵的方式表达，为：

$\begin{bmatrix} \dot{x}_1(t)\\ \dot{x}_2(t)\\ \dot{x}_3(t)\\ \vdots\\ \dot{x}_{n-1}(t)\\ \dot{x}_n(t) \end{bmatrix}= \begin{bmatrix} 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & 0 & \cdots & 1\\ -a_0 & -a_1 & -a_2 & -a_3 & \cdots & -a_{n-1} \end{bmatrix} \begin{bmatrix} x_1(t)\\ x_2(t)\\ x_3(t)\\ \vdots\\ x_{n-1}(t)\\ x_n(t) \end{bmatrix}+ \begin{bmatrix} 0\\ 0\\ 0\\ \vdots\\ 0\\ b \end{bmatrix}u(t)$

也即，

$\dot{x}(t)=Ax(t)+Bu(t)$

其中，

$A= \begin{bmatrix} 0 & 1 & 0 & 0 & \cdots & 0\\ 0 & 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & 0 & \cdots & 1\\ -a_0 & -a_1 & -a_2 & -a_3 & \cdots & -a_{n-1} \end{bmatrix} , B=\begin{bmatrix} 0\\ 0\\ 0\\ \vdots\\ 0\\ b \end{bmatrix}$

再回看Mass-Spring-Damper的例子：

$m\ddot{y}(t)+b\dot{y}(t)+ky(t) = u(t)$

我们设空间向量：

$x(t)=\begin{bmatrix} x_1(t)\\ x_2(t) \end{bmatrix}:=\begin{bmatrix} y(t)\\ \dot{y}(t) \end{bmatrix}$ ,

所以，

$\dot{x}(t)=\begin{bmatrix} \dot{y}(t)\\ \ddot{y}(t) \end{bmatrix} =\begin{bmatrix} \dot{y}(t)\\ -\frac{k}{m}y(t) -\frac{b}{m}\dot{y}(t)+\frac{1}{m}u(t)\end{bmatrix}$

也即

$\dot{x}(t)=\begin{bmatrix} x_2(t)\\ -\frac{k}{m}x_1(t) -\frac{b}{m}x_2(t)+\frac{1}{m}u(t)\end{bmatrix}= \begin{bmatrix} 0 & 1\\ -\frac{k}{m} & -\frac{b}{m} \end{bmatrix} \begin{bmatrix} x_1(t)\\ x_2(t)\end{bmatrix}+ \begin{bmatrix} 0\\ \frac{1}{m}\end{bmatrix}u(t)$

_ca_1cm_

关注

1
点赞
踩
1

收藏

觉得还不错? 一键收藏
1
评论
动态系统与控制原理（1）- 系统表达式

在上一篇博文中，我提到了，生活中方方面面都是动态系统，并稍微提了一下现代控制理论里的State-Space Representation。这篇博文将详细描述在现代控制理论中如何表示动态系统。既然你选择看这篇博文，你对于以下这张图肯定不陌生：对于系统（plant），变量是输入，是输出，可以代表系统的全部动态信息或者部分信息。上一篇博文提到了人口增长的例子：假设我们每年统计一次，上面的式子可以变为离散表达式：.我们再看一个例子（Mass-Spring-Damper）：...
复制链接

扫一扫