对比度受限的自适应直方图均衡化(CLAHE)

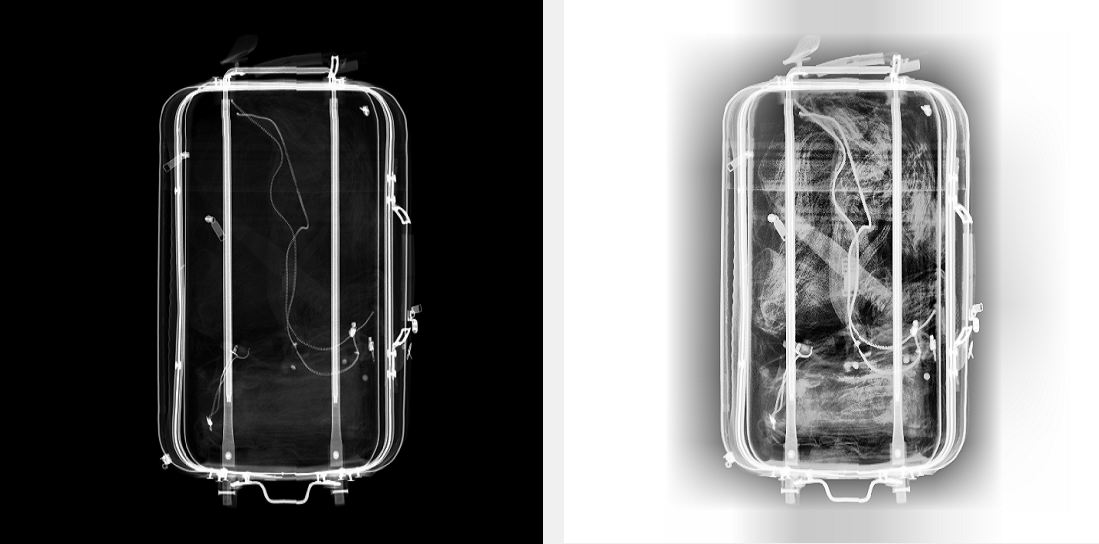
直方图均衡化（HE）是一种很常用的直方图类方法，基本思想是通过图像的灰度分布直方图确定一条映射曲线，用来对图像进行灰度变换，以达到提高图像对比度的目的。该映射曲线其实就是图像的累计分布直方图（CDF）（严格来说是呈正比例关系）。然而HE是对图像全局进行调整的方法，不能有效地提高局部对比度，而且某些场合效果会非常差。如：

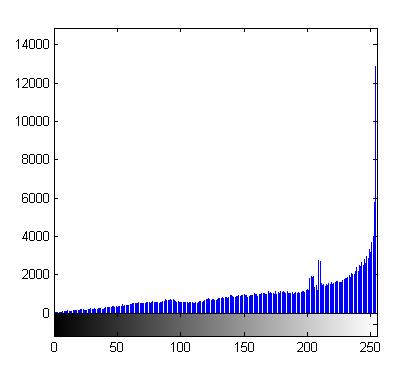
上述原图和HE结果图的直方图分别为：

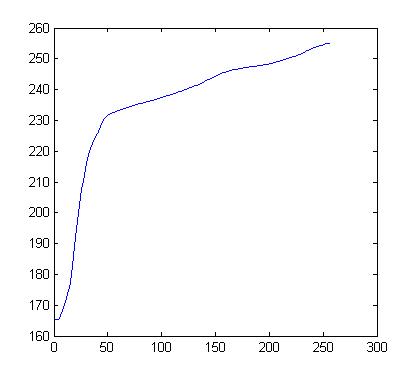
因为从原图的直方图中求取的映射函数（CDF）形状为：

将它作用于原图像会导致直方图被整体右移，没有充分利用整个灰度动态范围。

为了提高图像的局部对比度，有人提出将图像分成若干子块，对子块进行HE处理，这便是AHE（自适应直方图均衡化），使用AHE处理上图得到：

结果直方图：

可以看出结果图像的灰度较好地分布在了全部动态范围上。从结果图像上也可以看出，局部对比度的确得到了提高，视觉效果要优于HE。但是仍然有个问题：AHE对局部对比度提高过大，导致图像失真。看看背景区，本来的黑色背景现在已经变成白色了，原因是因为背景区中的局部子块统计得到的直方图在0灰度处幅值太高（实际上全黑子图基本上就集中在0灰度处），这样导致映射曲线斜率过高，将所有灰度值都映射到整个灰度轴的右侧，所以结果图中背景偏白（另外局部对比度过高还会放大图像中的噪声，不过上图并没有体现这一点）。

为了解决这个问题，我们必须对局部对比度进行限制，这就是我们今天的主题：CLAHE。

从HE中我们知道，映射曲线T与CDF关系为：（M为最高灰度值，N为像素个数）

限