一、原理:
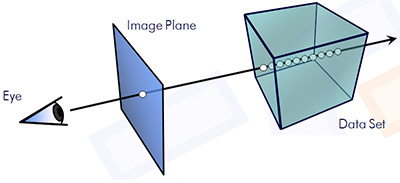
Levoy在1988年提出了光线投射(ray-casting)算法[1],其基本原理是:从屏幕上每一个像素点出发,沿着视线方向发射出一条光线,当这条光线穿过体数据时,沿着光线方向等距离采样,利用插值计算出采样点的颜色值和不透明度;接着按照从前到后或从后到前的顺序对光线上的采样点进行合成,计算出这条光线对应的屏幕上像素点的颜色值。其原理如图1所示。
图1光线投射原理
该算法基于射线扫描过程,符合人类生活常识,容易理解可以达到较好的绘制效果。因此光线投射是目前应用最为广泛的体绘制方法。然而当观察方向发生变化时,采样点的前后关系也必然变化,因此需要重新进行采样,计算量极为庞大。针对算法所存在的问题,人们提出了不少优化方法,如光线提前终止、利用空间数据结构来跳过无用的体素,如八叉树、金字塔、k-d树等。
该算法的流程图2所示。其中数据的分类主要是将体数据的标量值映射为颜色和不透明度,这需要构造合适的转换函数。对体数据的采样需要进行坐标系的变换,因为发射光线起点和方向是在图像空间描述的,而采样则是在物体空间进行的。图像空间到物体空间的转换可以通过旋转和平移操作实现。将光线的描述转换到物体空间后,沿着光线等间隔采样,采样点的颜色和不透明度通过插值获得。最后需要沿着光线对所有采样点的进行合成,得到光线对应的二维屏幕上像素点的颜色。
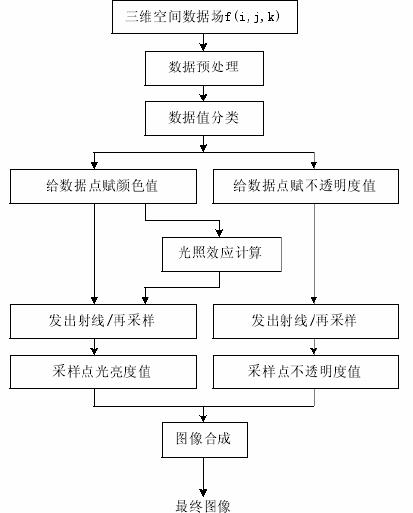
图2 光线投射流程
二、实现:
在实验中,我们绘制了一个人工生成的体数据,该体数据是一个大正方体,内部包含一个球体,球体内又包含一个小正方体。绘制结果如图3所示。
在数据分类阶段,我们简单地将三个几何体分别赋为白色、红色和黄色,并设置一定的透明度。我们选择了平行投影的方式,这样从图像平面发出的所有光线的方向都一致,因此在进行坐标变换时,光线方向的变换只需要进行一次。另外需要将每条光线的起点进行旋转和平移,以转换到物体空间描述。对采样点的插值采用的是三线性插值,这也是整个算法最耗时的部分。关于采样点的合成,我们采用从前向后的合成方式,合成公式如下:
这样可以利用提前终止条件以加速算法,即当累计不透明度超过1时就停止合成操作。
从实验结果可以看出,光线投射法通过不透明度的设置可以得到半透明的绘制效果,这样就能有效地反映出物体内部结构,这也是体绘制与面绘制的最大区别。光线投射法作为最为通用的体绘制方法,其绘图质量最高,但相应的问题就是绘制速度较低,难以实时化。实际上,对于本实验中的体积数据,使用简单的最近邻插值得到的结果与三线性插值并没有差异,而且速度上能提高不少。因为在该体数据中,对大部分采样点来说,与其邻近的八个数据点的值都是相同的。
图3 光线投射实验结果
(注:核心代码纯C,图像显示部分使用了OpenGL)
参考:
[1] Levoy M. Display of surfaces from volumedata[J]. Computer Graphics and Applications, IEEE, 1988, 8(3): 29-37.










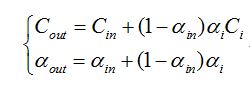
















 1833
1833

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










