poj 2488 字典序搜索 No matter the ending is perfect or not, you cannot disappear from my world

A Knight's Journey

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 26645		Accepted: 9091

Description

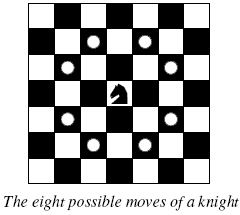Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

Source

TUD Programming Contest 2005 , Darmstadt, Germany

 

 

 

 

 

这个题目的意思是说有一个骑士，他想要走遍所有位置，问是否可以实现，我们在做这

 

个题目的时侯要用搜索来做，我们可以数走的个数，看是否可以实现使其等于P*Q，这

 

样就可以了呗，但是最变态的竟然要求按照字典序顺序走，也就是说我们要按照字典序

 

的顺序走一遍，所以我们要从A1开始走，而且国际象棋是横着是字母，竖着才是数字，

 

所以我们按照照顾横着的原则，要选择d[x]=-2，-1,1，2，这样的原则来写，其实也就是

 

按照字典序了，还有一个问题，我们用x来数数，所以x<q，而不是x<p,这个地方害的我

 

WA了很多遍

 

 

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int p,q;
static int dis[8][2]={-2, -1, -2, 1, -1, -2, -1, 2, 1, -2, 1, 2, 2, -1, 2, 1};//方向
char map[100];
int s[30][30];//标记数组
int dfs(int x,int y,int num)
{

    if(num==p*q)
    return 1;
    int i;
    int x1,y1;
    for(i=0;i<8;i++)
    {
        x1=x+dis[i][0];
        y1=y+dis[i][1];
        if((x1>=0)&&(x1<q)&&(y1>=0)&&(y1<p)&&(s[y1][x1]==0))
        {
            s[y1][x1]=1;
            map[num*2]=x1+'A';
            map[num*2+1]=y1+'1';
            if(dfs(x1,y1,num+1))
            return 1;
            s[y1][x1]=0;

        }
    }
    return 0;

}




int main()
{
    int t,T;
    scanf("%d",&T);
     int i;
    for(t=1;t<=T;t++)
    {
      scanf("%d%d",&p,&q);
      memset(s,0,sizeof(s));
      memset(map,0,sizeof(map));
      s[0][0]=1;
      map[0]='A';
      map[1]='1';
      printf("Scenario #%d:\n",t);
      if(dfs(0,0,1))
      {

          for(i=0;i<strlen(map);i++)
          {
              printf("%c",map[i]);
          }
          printf("\n\n");


      }
      else
      {
          printf("impossible\n\n");

      }


    }
    return 0;
}