范数,是具有“长度”概念的函数。在线性代数、泛函分析及相关的数学领域,是一个函数,其为向量空间内的所有向量赋予非零的正长度或大小。半范数反而可以为非零的向量赋予零长度。
举一个简单的例子,一个二维度的欧氏几何空间 就有欧氏范数。在这个向量空间(譬如:(3,7))的元素常常在笛卡儿座标系统被画成一个从原点出发的箭号。每一个向量的欧氏范数就是箭号的长度。
就有欧氏范数。在这个向量空间(譬如:(3,7))的元素常常在笛卡儿座标系统被画成一个从原点出发的箭号。每一个向量的欧氏范数就是箭号的长度。
拥有范数的向量空间就是赋范向量空间。同样,拥有半范数的向量空间就是赋半范向量空间。
定义
假设V是域F上的向量空间;V的半范数是一个函数 ,满足:
,满足:
 ,
,
 (正值性)
(正值性) (正值齐次性)
(正值齐次性)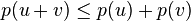 (三角不等式)
(三角不等式)
范数是一个半范数加上额外性质:
如果拓扑向量空间的拓扑可以被范数导出,这个拓扑向量空间被称为赋范向量空间。
例子
欧几里德范数
在n维欧几里德空间Rn上,向量x =(x1, x2, ..., xn)的最符合直觉的长度由以下公式给出
根据勾股定理,它给出了从原点到点x之间的(通常意义下的)距离。 欧几里德范数是Rn上最常用的范数,但正如下面举出的,Rn上也可以定义其他的范数。然而,以下定义的范数都定义了同一个拓扑结构,因此它们在某种意义上都是等价的。
在一个n维复数空间Cn中,最常见的范数是:
其中x是一个列向量([x1; x2; ...; xn]),而x*表示其共轭转置。
以上公式适用于任何内积空间,包括欧式空间和复空间。在欧几里得空间里,内积等价于点积,因此公式可以写成以下形式:
特别地,Rn+1中所有的欧几里得范数为同一个给定正实数的向量的集合是一个n维球面。
复数的欧几里得范数
如果将复平面看作欧几里得平面R2,那么复数的欧几里得范数是其绝对值(又称为模)。这样,我们可把x + iy视为欧几里得平面上的一个向量,由此,这个向量的欧几里得范数即为 (最初由欧拉提出)。
(最初由欧拉提出)。







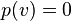 ,当且仅当
,当且仅当
 是
是
 。
。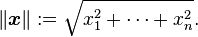



















 727
727

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








