C++徒手撸多层感知机(MLP)训练MNIST数据集

1. 模型建立

1.1 基本单位–层

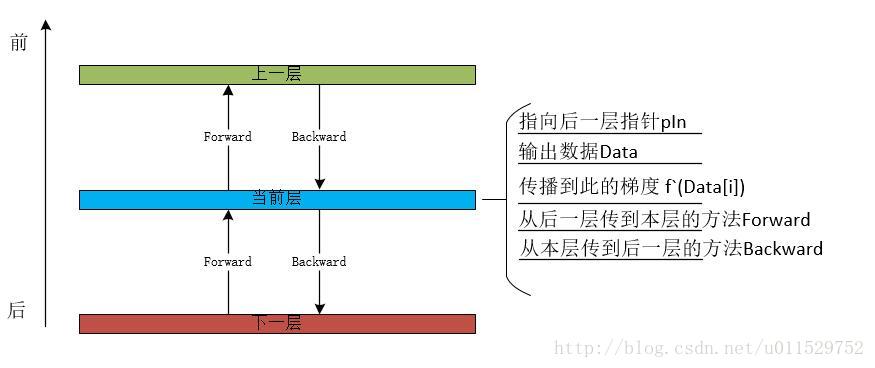
神经网络可以抽象为层：

每个层的作用是把自己后面那一层的数据，通过前向计算到自己层的数据中，并把积累到自己的残差，后向计算到自己的下一层中，于是层与层之间可以是链表的结构。每一层只需它的后一层的指针或者引用就可以了。

为了简单起见，在所有的讨论中都不加入caffe的blob或者Tensorflow和Torch的张量的概念。后续如果讨论卷积层则必须要引入，所以本章中所有的输入输出均是一维的数据，都看作一维向量。

1.1.1 输入层

输入层没有反向和正想向传播，因为输入层是最后一层，按照上面的定义forward和backward为空。只需要提供一个接口，把输入的数据给包起来。即只有个data成员。

1.1.2 损失层

损失层是最后一层，损失层的正向传播就是把后一层的输出和教师信号(label)数据计算成损失值。反向传播是计算到下一层的输出。即损失函向后链式法则的最外层。如果损失函数是$J=\sum_i \dfrac{1}{2}(y_i-t_i)^2$,那么后向传播就应该是对$y_i$的导数$\partial J/\partial y_i =y_i-t_i$ 。损失层还需要保留一个教师信号的引用来计算损失。

1.1.3 激活层

激活层的作用就是把输入的值按照激活函数激活输出，这就是forward。反向传播则是将传到自己层的梯度乘上激活函数的偏导。

如果是用sigmoid函数激活，$out_i=\dfrac{1}{1+exp(-in_i)}$，$\dfrac{\partial out_i}{int_i}=out_i(1-out_i)$ 。如果是softmax函$out_i=\dfrac{in_i}{\sum_j exp(in_j)}$数，偏导和sigmoid是一样的。只不过$out_i$的含义变了。

1.1.4 全连接层

全链接层的正向传播就是:

$$forward:out_i=\sum_{j=1}^{m}W_{ij}in_j +W_{i0}*1$$
反向传播是著名的BP :
$$backward:\dfrac{\partial J}{\partial in_j}=\sum_{i=1}^{n}W{ij}*\dfrac{J}{out_i}$$
至于 $W_{i,j}$的参数调整放到优化方法中去。

1.2 网络

把所有的层组合起来就成了网络，为了简单起见，网络中存放：

1. 各层的指针数组。
2. 层数
3. 网络的前向传播，forward，从后向前各层依次前向传播
4. 网络的后向传播，backward，从前向后依次后向传播
5. 网络所有的梯度清零，zeroDelta，应用于批次，把积累的梯度清零（实际并没有用，因为优化方法里不需要这个项）

1.3 优化方法

准备采用adam优化，adam优化保留了动量项。adam认为如果一个参数调整的方向应该是当前的梯度和之前梯度积累方向的加权，即之前的优化方向影响现在的优化方向。同时adam认为如果当前梯度变化的绝对值或平方项和之前的梯度变化绝对值或平方项加权后过大，则不应该调整得过长，越陡的地方越要小心。

adam的一次优化过程如下:

$$g_t=\dfrac{\partial J_t}{\partial w_{i,j}}\\ m_t=u*m_{t-1}+(1-u)*g_t\\ n_t=v*n_{t-1}+(1-v)*g_t^2\\ \hat{m_t}=m_t/(1-u)\\ \hat{n_t}=n_t/(1-v)\\ \Delta w_{i,j}=\eta*\dfrac{\hat{m_t}}{\sqrt{\hat{n_t}}+\epsilon}$$
其中u，v为加权系数， $\epsilon$是一个极小值。

优化方法类中，存放一个指向一个包含每个需要调整参数中间记录的结构，结构中记录$m_t,n_t,g_t$。在批次调整的时候，一批中每次后向传播之后都要累加$g_t$,最后取平局的方向作为最终的$g_t$,所以优化方法还需要记录批次大小batch_size。$g_t$每个批次积累，新批次开始的时候清零。

2. 代码构建

环境是win10 64位，VS2013，C++。使用到的标准库

#include <assert.h>
#include <iostream>
#include <math.h>
#include <assert.h>
#include <stdlib.h>
#include <time.h>
#include <limits>
#include <string>

2.1 层

class my_Layer{
public:
    //定义成员变量
    int n=0;    //本层输出维度数
    int m=0;    //输入数据的维度数
    my_Layer *pIn = nullptr;    //输入的层的指针
    std::vector<double> data;   //输出数据
    std::vector<double> delta;
    std::string name = "baseLayer";
public:
    my_Layer(){}
    virtual ~my_Layer(){}
    virtual void forward(){};
    virtual void backward(){};
    virtual void zeroDelta(){
        int n = delta.size();
        for (int i = 0; i < n;++i){
            delta[i] = 0;
        }
    }
};

所有的具体层都派生自这一层

2.1.1 输入层

定义：

//输入层
class my_inputLayer :public my_Layer{
public:
    my_inputLayer(){}
    my_inputLayer(double* pIn,int n);
    my_inputLayer(std::vector<double>& pIn, int n);
    virtual ~my_inputLayer(){}
};

实现

//输入层
my_inputLayer::my_inputLayer(double* pIn, int n){
    name = "inputLayer";
    data = std::vector<double>(pIn,pIn+n);
    this->m = n;
    this->n = n;
}
my_inputLayer::my_inputLayer(std::vector<double>& vIn, int n){
    name = "inputLayer";
    data = vIn;
    this->m = n;
    this->n = n;
}

2.1.2 损失层

定义

class my_lossLayer :public my_Layer{
public:
    std::vector<double> *pT=nullptr; //教师信号
public:
    my_lossLayer(){}
    my_lossLayer(my_Layer * pIn);
    virtual ~my_lossLayer(){}
    bool setTeacher(std::vector<double> *pT);   //设置教师信号
    virtual void forward();
    virtual void backward();
};

实现 损失层使用的是平方损失项

//损失层
my_lossLayer::my_lossLayer(my_Layer * pIn){
    name = "lossLayer";
    this->pIn = pIn;
    this->m = pIn->n;
    this->n = 1;
    data = std::vector<double>(n);
    delta = std::vector<double>(n);
}

bool my_lossLayer::setTeacher(std::vector<double> *vT){
    if (vT->size() != m){
        return false;
    }
    this->pT = vT;
}
void my_lossLayer::forward(){
    assert(m > 1);
    assert(n == 1);
    assert(pIn->data.size() == m);
    assert(pT->size() == m);
    data[0] = 0;
    double tm = 0;
    for (int i = 0; i < m; ++i){
        tm = pIn->data[i] - (*pT)[i];
        data[0] += tm*tm;
    }
    data[0] *= 0.5;
    delta[0] = 1.0;
}
void my_lossLayer::backward(){
    assert(m > 1);
    assert(n == 1);
    assert(pIn->delta.size() == m);
    assert(pT->size() == m);
    for (int i = 0; i < m; ++i){
        pIn->delta[i] = pIn->data[i] - (*pT)[i];
    }
}

2.1.3 激活层

定义，激活层使用的是sigmoid层，另还有一个softmax层

//激活层
class my_activeLayer :public my_Layer{
public:
    my_activeLayer(){}
    my_activeLayer(my_Layer * pIn);
    virtual ~my_activeLayer(){}
    virtual void forward();
    virtual void backward();
};
//softmax层
class my_softmaxLayer :public my_Layer{
public:
    my_softmaxLayer(){}
    my_softmaxLayer(my_Layer * pIn);
    virtual ~my_softmaxLayer(){}
    virtual void forward();
    virtual void backward();
};

实现

//激活层
my_activeLayer::my_activeLayer(my_Layer * pIn){
    name = "activeLayer";
    this->pIn = pIn;
    this->m = pIn->n;
    this->n = this->m;
    data = std::vector<double>(n);
    delta = std::vector<double>(n);
}

void my_activeLayer::forward(){
    assert(m > 1);
    assert(n > 1);
    assert(m == n);
    assert(pIn->data.size() == m);
    assert(data.size() == n);
    for (int i = 0; i < m; ++i){
        data[i] = 1.0 / (1.0 + exp(-pIn->data[i]));
    }
}

void my_activeLayer::backward(){
    assert(m > 1);
    assert(n > 1);
    assert(m == n);
    assert(delta.size() == n);
    assert(pIn->delta.size() == m);
    assert(data.size() == n);
    for (int i = 0; i < m; ++i){
        (pIn->delta)[i] = delta[i]*data[i]*(1 - data[i]);
    }
}

//softmax层
my_softmaxLayer::my_softmaxLayer(my_Layer * pIn){
    name = "activeLayer";
    this->pIn = pIn;
    this->m = pIn->n;
    this->n = this->m;
    data = std::vector<double>(n);
    delta = std::vector<double>(n);
}

void my_softmaxLayer::forward(){
    assert(m > 1);
    assert(n > 1);
    assert(m == n);
    assert(pIn->data.size() == m);
    assert(data.size() == n);
    double sum = 0;
    for (int i = 0; i < m; ++i){
        sum += exp(pIn->data[i]);
    }
    for (int i = 0; i < m; ++i){
        data[i] = exp(pIn->data[i])/(sum+eps); 
    }
}

void my_softmaxLayer::backward(){
    assert(m > 1);
    assert(n > 1);
    assert(m == n);
    assert(delta.size() == n);
    assert(pIn->delta.size() == m);
    assert(data.size() == n);
    for (int i = 0; i < m; ++i){
        (pIn->delta)[i] = delta[i] * data[i] * (1 - data[i]);
    }
}

2.1.4 全连接层

定义

//全链接层
class my_bpLayer:public my_Layer{
public:
    //定义成员变量
    std::vector<std::vector<double> >W; //权值 n*(m+1) 权值是要给优化方法修改的   
public:
    //定义成员函数
    my_bpLayer(){}
    my_bpLayer(my_Layer * pIn,int n);   //
    virtual ~my_bpLayer(){}
    virtual void forward();
    virtual void backward();
};

实现

my_bpLayer::my_bpLayer(my_Layer * pIn,int n){
    name = "bpLayer";
    this->pIn = pIn;
    this->m = pIn->n;
    this->n = n;
    data = std::vector<double>(n);
    delta = std::vector<double>(n);
    W = std::vector<std::vector<double> >(n, std::vector<double>(m + 1));
    //权值初始化
    srand(time(0));
    //产生[-0.1到0.1]的随机浮点数,精度是1/2000
    for (int i = 0; i<W.size(); ++i){
        for (int j = 0; j<W[i].size(); ++j){
            W[i][j] = double(rand() % 2000 - 1000) / 10000.0;
        }
    }
}

void my_bpLayer::forward(){
    assert(m > 1);
    assert(n > 1);
    assert(pIn->data.size() == m);
    assert(data.size() == n);
    for (int i = 0; i < n; ++i){
        data[i] = 0;
        for (int j = 0; j < m; ++j){
            data[i] += pIn->data[j] * W[i][j];
        }
        data[i] += W[i][m]; //偏置
    }

}
void my_bpLayer::backward(){
    assert(m > 1);
    assert(n > 1);
    assert(pIn->delta.size() == m);
    assert(delta.size() == n);
    //可以优化
    for (int j = 0; j < m; ++j){
        pIn->delta[j] = 0;  //delta会累加
        for (int i = 0; i < n; ++i){
            pIn->delta[j] += W[i][j] * delta[i];
        }
    }
}

2.2 网络

定义

#pragma once
#include"my_Layers.h"
//网络类，定义网络
class my_mlp{       
public:
    //成员
    unsigned int num_layers;    //层数
    std::vector<my_Layer*>pLayers;  //层的指针
public:
    my_mlp();
    virtual ~my_mlp();
    virtual void buildNet(int m);   //传入输入层大小
    virtual void forward();     //整体前向输出
    virtual void backward();        //后向传播
    virtual void zeroDelta();   //清理梯度
};

实现

#include "my_Layers.h"
#include"my_mlp.h"
#include <assert.h>
my_mlp::my_mlp(){
    num_layers = 0;
}
my_mlp::~my_mlp(){
    for (auto i : pLayers){
        delete i;
    }
}
void my_mlp::forward(){
    for (int i = 1; i < num_layers; ++i){
            pLayers[i]->forward();
    }
}

void my_mlp::backward(){
    for (int i = num_layers - 1; i>1; --i){ //输入层的上一层不往输入层反向传播
            pLayers[i]->backward();
    }
}
void my_mlp::zeroDelta(){
    for (int i = num_layers - 1; i >= 0; --i){
        pLayers[i]->zeroDelta();
    }
}
void my_mlp::buildNet(int m){
    std::vector<double> pIn(m);
    //双隐层
    my_Layer * input = new my_inputLayer(pIn, m);
    pLayers.push_back(input); ++num_layers;
    my_Layer * connect1 = new my_bpLayer(input, 512);
    pLayers.push_back(connect1); ++num_layers;
    my_Layer * active1 = new my_activeLayer(connect1);
    pLayers.push_back(active1); ++num_layers;
    my_Layer * connect2 = new my_bpLayer(active1, 256);
    pLayers.push_back(connect2); ++num_layers;
    my_Layer * active2 = new my_activeLayer(connect2);
    pLayers.push_back(active2); ++num_layers;
    my_Layer * connect3 = new my_bpLayer(active2, 10);
    pLayers.push_back(connect3); ++num_layers;
    my_Layer * softmax = new my_softmaxLayer(connect3);
    pLayers.push_back(softmax); ++num_layers;
    my_Layer * loss = new my_lossLayer(softmax);
    pLayers.push_back(loss); ++num_layers;


    //单隐层
    //my_Layer * input = new my_inputLayer(pIn, m);
    //pLayers.push_back(input); ++num_layers;

    //my_Layer * connect1 = new my_bpLayer(input, 512);
    //pLayers.push_back(connect1); ++num_layers;

    //my_Layer * active1 = new my_activeLayer(connect1);
    //pLayers.push_back(active1); ++num_layers;

    //my_Layer * connect3 = new my_bpLayer(active1, 10);
    //pLayers.push_back(connect3); ++num_layers;

    my_Layer * active3 = new my_activeLayer(connect3);
    pLayers.push_back(active3); ++num_layers;
    //my_Layer * softmax = new my_softmaxLayer(connect3);
    //pLayers.push_back(softmax); ++num_layers;

    //my_Layer * loss = new my_lossLayer(softmax);
    //pLayers.push_back(loss); ++num_layers;
}

2.3 优化方法

定义

#pragma once
#include "my_Layers.h"
#include"my_mlp.h"
struct optim_stc{
    my_bpLayer* pLayer;
    std::vector<std::vector<double> > mt;   //冲量矩阵n*m
    std::vector<std::vector<double> > nt;   //二阶矩阵
    std::vector<std::vector<double> > gt;   //记录梯度的改变的累加
};
class my_optim{
public:
    my_optim() :ita(0.1),u(0.5),v(0.5),batch_size(1.0){};
    my_optim(my_mlp * pNet,double ita,double u,double v,double batch_size);
    virtual ~my_optim();
    virtual void adjustW(); //调整权值
    virtual void update();  //跟新冲量矩阵。
public:
    std::vector<optim_stc*> vOpt;   //所有需要调整权值的层和冲量项等
    double ita; //学习率
    double u;   //冲量项的权
    double v;   //梯度二阶的权
    double batch_size;
};

实现

#include "my_optim.h"
my_optim::my_optim(my_mlp * pNet,double ita,double u,double v,double batch_size){
    this->ita = ita;
    this->u = u;
    this->v = v;
    this->batch_size = batch_size;
    for (auto i : pNet->pLayers){
        if (i->name == "bpLayer"){
            optim_stc *tm = new optim_stc;
            tm->pLayer = dynamic_cast<my_bpLayer*>(i);
            tm->mt = std::vector<std::vector<double> >(i->n, std::vector<double>(i->m+1));
            tm->nt = std::vector<std::vector<double> >(i->n, std::vector<double>(i->m+1));
            tm->gt = std::vector<std::vector<double> >(i->n, std::vector<double>(i->m + 1));
            vOpt.push_back(tm);
        }
    }
}
my_optim::~my_optim(){
    for (auto Opt : vOpt){
        delete Opt;
    }
}
void my_optim::adjustW(){
    double gt = 0;
    for (auto opt : vOpt){
        for (int i = 0; i < opt->pLayer->n; ++i){
            int m = opt->pLayer->m;
            for (int j = 0; j <m; ++j){//adam
                gt = opt->gt[i][j]/batch_size;
                opt->gt[i][j] = 0;//调整完置零
                opt->mt[i][j] = u*opt->mt[i][j] +(1.0 - u) *gt;
                opt->nt[i][j] = sqrt(v*opt->nt[i][j]+(1.0 - v)*gt*gt);
                double mtt = opt->mt[i][j] / (1.0 - u);
                double ntt = opt->nt[i][j] / sqrt(1.0 - v);
                opt->pLayer->W[i][j] -= ita*mtt / (eps + ntt);  
            }
            gt = opt->gt[i][m] / batch_size;
            opt->mt[i][m] = u*opt->mt[i][m] / (1.0 - v) + gt;
            opt->nt[i][m] = sqrt(v*opt->nt[i][m] / (1.0 - v) + gt*gt);
            opt->pLayer->W[i][m] -= ita*opt->mt[i][m] / (eps + opt->nt[i][m]);
        }
    }
}
void my_optim::update(){
    for (auto opt : vOpt){
        for (int i = 0; i < opt->pLayer->n; ++i){
            double delta_t = opt->pLayer->delta[i];
            std::vector<double> & pData = opt->pLayer->pIn->data; //下一层的数据
            int m = opt->pLayer->m;
            for (int j = 0; j <m; ++j){
                opt->gt[i][j] += delta_t*pData[j];
            }
            opt->gt[i][m] = delta_t;    //调整偏置的权
        }
    }
}

3. 试验的构建

3.1 解析MNIST

原理略，MNIST的格式参考MNIST官网,直接上代码,注意其中的编码方式，MNIST的int是高位在后的。

unsigned char * loadMnistData(const char * filename,  int &row,  int &col,  int &num);
unsigned char * loadMnistLabel(const char * filename, int &num);
void freeMnist(unsigned char * pData, unsigned char * pLabel);

#include<iostream>
#include<fstream>
#include<algorithm>
using namespace std;
unsigned char * loadMnistData(const char * filename, int &row, int &col, int &num){
    ifstream file(filename,ios::binary);    //二进制形式打开文件
    if (!file)return nullptr;
    unsigned char buffer[4];
    row = 0; col = 0; num = 0;
    file.seekg(0, ios::beg);

    file.read((char*)&buffer,4);
    int type = 0;
    for (int i = 3, k = 1; i >= 0; --i, k *= 256)
        type += k*buffer[i];
    if (type != 2051){
        return nullptr;
    }

    file.read((char*)&buffer, 4);
    for (int i = 3,  k = 1; i >= 0; --i, k *= 256)
        num += k*buffer[i];

    file.read((char*)buffer, 4);
    for (int i = 3,  k = 1; i >= 0; --i, k *= 256)
        row += k*buffer[i];

    file.read((char*)buffer, 4);
    for (int i = 3,  k = 1; i >= 0; --i, k *= 256)
        col += k*buffer[i];

    unsigned char * pData = new unsigned char[num*row*col];
    int size = row*col*num;
    file.read((char*)(pData), size);

    return pData;
}

unsigned char * loadMnistLabel(const char * filename, int &num){
    ifstream file(filename, ios::binary);   //二进制形式打开文件
    if (!file)return nullptr;
    unsigned char buffer[4];
    num = 0;
    file.seekg(0, ios::beg);

    file.read((char*)&buffer, 4);
    int type = 0;
    for (int i = 3, k = 1; i >= 0; --i, k *= 256)
        type += k*buffer[i];
    if (type != 2049){
        return nullptr;
    }

    file.read((char*)&buffer, 4);
    for (int i = 3, k = 1; i >= 0; --i, k *= 256)
        num += k*buffer[i];
    unsigned char * pData = new unsigned char[num];
    file.read((char*)(pData), num); 

    return pData;
}

void freeMnist(unsigned char * pData, unsigned char * pLabel){
    delete[] pData; pData = nullptr;
    delete[] pLabel; pLabel = nullptr;
}

3.2 试验流程

偷懒并没有写存放网络和载入网络的接口，所以流程就是训练完直接测试。

使用了opencv2.4.9来测试MNIST文件是否解析正确。

网络的输入时28*28=784维的向量，即把图像看为一维指针，逐行串联起来。

最底层是输入层，包裹着784维输入数据。

第一个全连接层输入时784，输出是512;

然后连接激活层，sigmoid激活层。

第二个全连接层输入时512，输出是256;

然后连接一个sigmoid激活层。

第三个全连接层，输入时256，输出是10。

然后连接softmax层，10个输入10个输出，输出代表(0,1,2,3,4….)的概率。

代码就是2.2中网络类的buildNet中的代码。

试验的主函数：

#include<iostream>
#include"my_mlp.h"
#include"loadMnist.h"
#include"opencv.hpp"
#include"my_optim.h"
#include <iomanip>
using namespace std;

int main(){
    //
    int num,numl, row, col;
    unsigned char *pData = loadMnistData("E:\\DataSets\\Mnist\\train-images.idx3-ubyte", row,col,num);
    unsigned char *pLabel = loadMnistLabel("E:\\DataSets\\Mnist\\train-labels.idx1-ubyte", numl);
    int imgsize = row*col;
    if (numl != num){
        return 0;
    }
    cout << num << " " << row << " " << col << endl;
    //可视化
    //int R, C;
    //if (num == 60000){
    //  R = 300;
    //  C = 200;
    //}
    //else if (num == 10000){
    //  R = 100; C = 100;
    //}
    //cv::Mat img(R*row, C*col, CV_8UC1);

    //for (int r = 0; r < R; ++r){
    //  for (int c = 0; c < C; ++c){
    //      //cout <<(int) pLabel[r*C + c] << " ";
    //      for (int i = 0; i < row; ++i){
    //          for (int j = 0; j < col; ++j){
    //              img.at<unsigned char>(r*row+i,c*col+j) = *(pData +(r*C+c)*imgsize+ i*col + j);
    //              //cout << (int)img.at<unsigned char>(i, j) << " ";
    //          }
    //          //cout << endl;
    //      }
    //  }
    //  //cout << endl;
    //}
    //cv::namedWindow("img",0);
    //cv::imshow("img", img);
    //cv::waitKey();

    //构建神经网络
    my_mlp mlp;
    mlp.buildNet(imgsize);
    //超参数
    double ita = 0.01;  
    double u = 0.1;
    double v = 0.01;
    int batch_size = 18;
    //构建训练对象
    my_optim opt(&mlp,ita,u,v,batch_size);
    std::vector<double> &pIn = mlp.pLayers[0]->data;


    //开始训练//
    unsigned char * pImg = pData;
    //取出损失层
    my_lossLayer * ploss = dynamic_cast<my_lossLayer *>(mlp.pLayers[mlp.num_layers - 1]);
    vector<double>& pOut = mlp.pLayers[mlp.num_layers - 2]->data;
    int id_img = 0;
    double loss_batch = 0;
    int id = 0;
    double max = pOut[0];
    //训练的轮数
    int epoch = 1;
    int ie = 0;
    //设置输出流
    cout << setiosflags(ios::fixed) << setprecision(3);
    while (ie<epoch&&id_img < num){
        loss_batch = 0;
        for (int i = 0; i < batch_size; ++i){
            pImg = pData + id_img*imgsize;
            //取一幅图像
            for (int i = 0; i < imgsize; ++i){
                pIn[i] = (double)pImg[i]/255.0;
            }
            //取得图像的label
            std::vector<double> pT(10);
            pT[pLabel[id_img]] = 1.0;

            //**************
            cv::Mat img(row, col, CV_8UC1);
            for (int i = 0; i < row; ++i){
                for (int j = 0; j < col; ++j){
                    img.at<unsigned char>(i, j) = *(pImg + i*col+j);

                }
            }
            cv::imshow("img", img);
            cv::waitKey(10);
            //****************


            //一次传播往返
            ploss->setTeacher(&pT);//要先设置教师信号
            for (auto i : pT){
                cout << i << " ";
            }
            cout << endl;

            mlp.forward();

            //预测值
            max = pOut[0];
            id = 0;
            cout << pOut[0] << " ";
            for (int i = 1; i<10; ++i){
                cout << pOut[i] << " ";
                if (pOut[i] > max){
                    max = pOut[i];
                    id = i;
                }
            }
            cout << endl;           
            cout << ploss->data[0] << " " << (int)pLabel[id_img]<<" "<< id << " " << endl;  //取得损失          
            mlp.backward();
            opt.update();
            loss_batch += ploss->data[0];
            ++id_img;
        }       
        cout << loss_batch / (double)batch_size  << " " << id << " " << (int)pLabel[id_img] << " " << id_img << "/" << num << endl;

        //id_img = 0;
        opt.adjustW();
        //mlp.zeroDelta();
        if (id_img+batch_size >= num){
            id_img = id_img+batch_size-num;
            ++ie;
            continue;
        }
    }

    //释放空间
    delete[] pData;
    delete[] pLabel;

    //***********预测*************************************************
    pData = loadMnistData("E:\\DataSets\\Mnist\\t10k-images.idx3-ubyte", row, col, num);
    pLabel = loadMnistLabel("E:\\DataSets\\Mnist\\t10k-labels.idx1-ubyte", numl);
    imgsize = row*col;
    if (numl != num){
        return 0;
    }
    cout << num << " " << row << " " << col << endl;
    id_img = 0;
    int numc = 0;
    while (id_img < num){
        loss_batch = 0;
        pImg = pData + id_img*imgsize;
        //取一幅图像
        for (int i = 0; i < imgsize; ++i){
            pIn[i] = (double)pImg[i] / 255.0;
        }
        //取得图像的label
        std::vector<double> pT(10);
        pT[pLabel[id_img]] = 1.0;

        //**************
        cv::Mat img(row, col, CV_8UC1);
        for (int i = 0; i < row; ++i){
            for (int j = 0; j < col; ++j){
                img.at<unsigned char>(i, j) = *(pImg + i*col + j);

            }
        }
        cout << (int)pLabel[id_img] << endl;
        cv::imshow("img", img);
        cv::waitKey(10);
        //****************

        //一次传播往返
        ploss->setTeacher(&pT);//要先设置教师信号
        mlp.forward();

        max = pOut[0];
        id = 0;
        for (int i = 1; i<10; ++i){
            if (pOut[i] > max){
                max = pOut[i];
                id = i;
            }
        }
        cout << (int)pLabel[id_img] << " "<<id << " " ;
        if (id == pLabel[id_img]){
            ++numc;
        }
        cout << double(numc) / double(id_img + 1) <<" "<< id_img << "/" << num << endl;
        ++id_img;
    }


    cv::waitKey();
    freeMnist(pData, pLabel);
    return 0;
}

3.3 试验效果

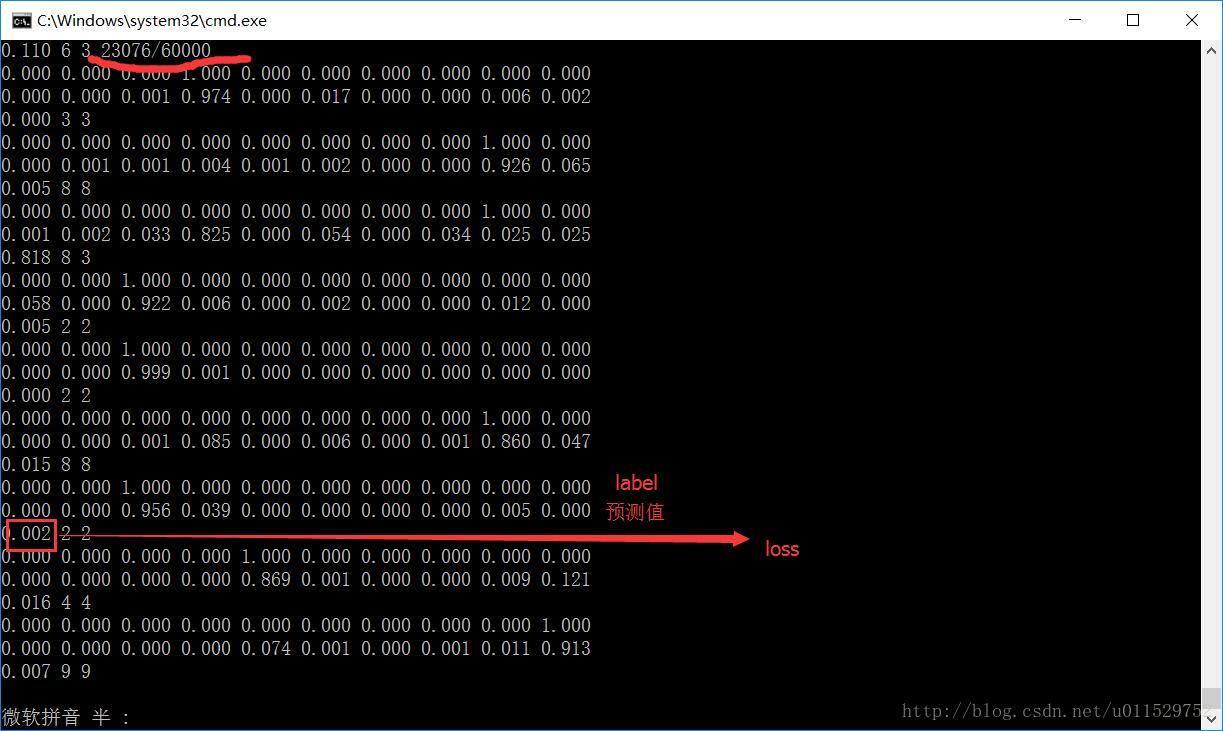
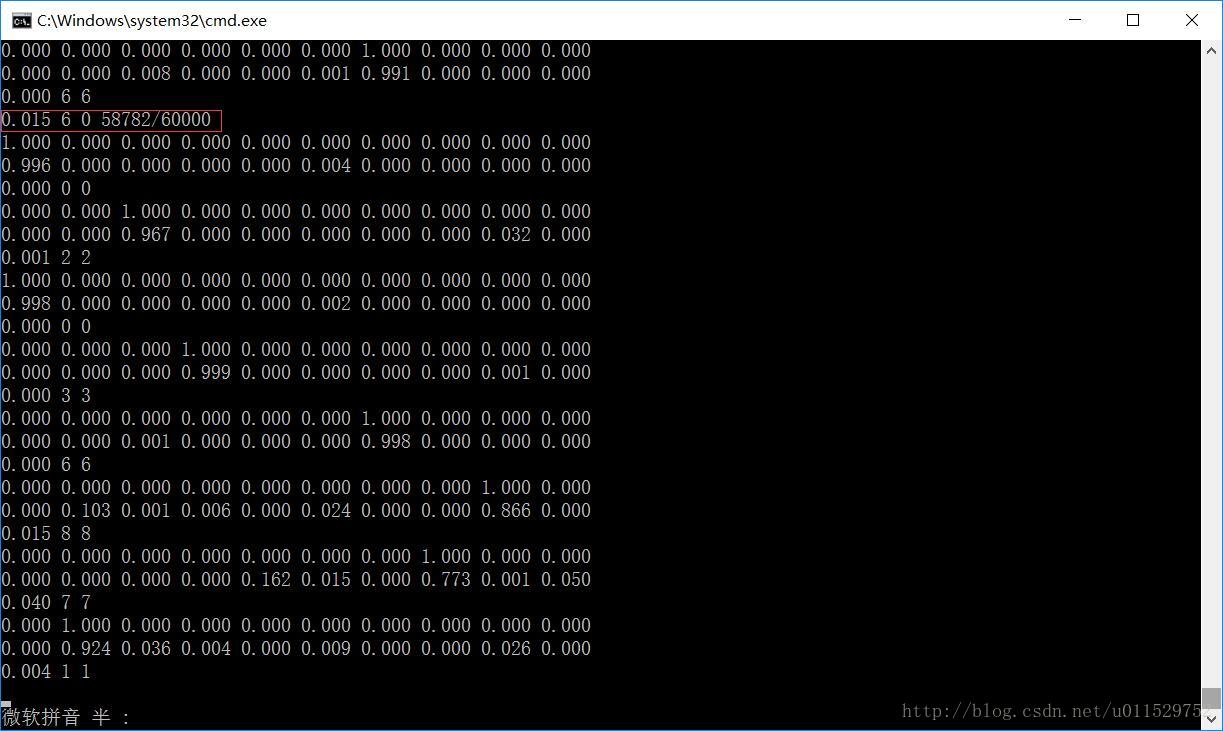
训练过程：

测试过程

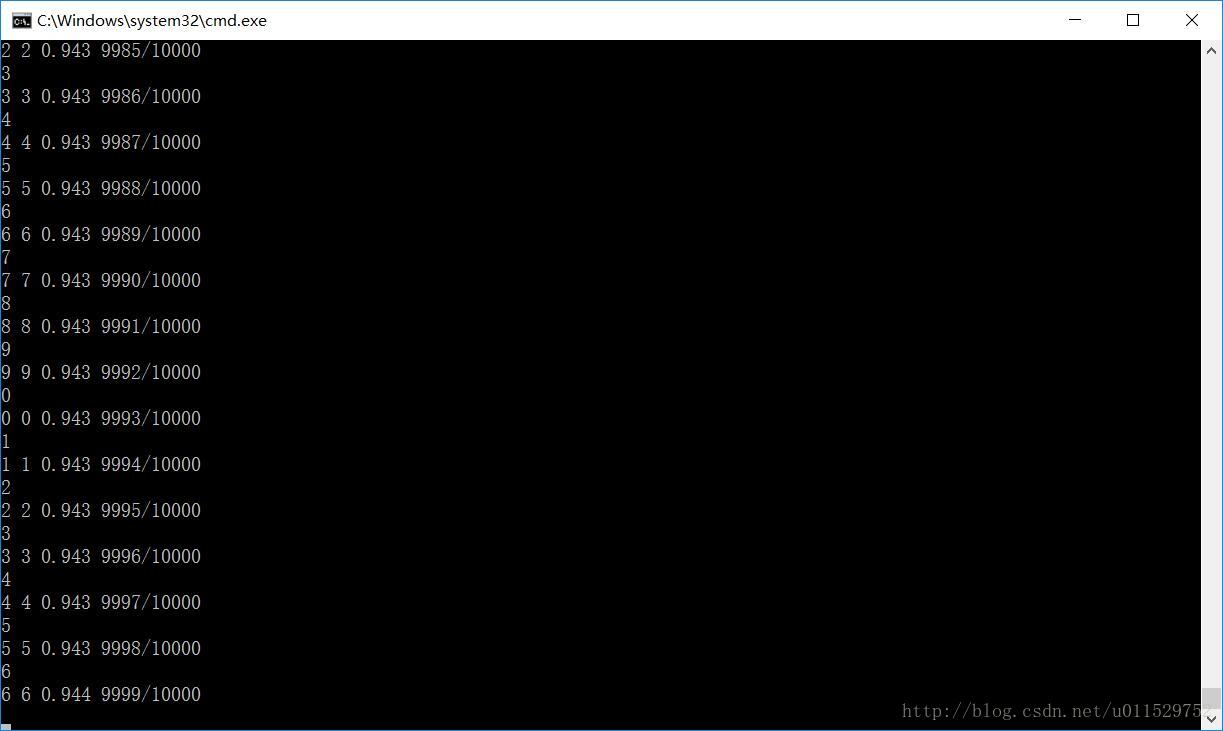
最后测试集的正确率94.3%。

4. 不足和展望

1. 没有定义输入输出接口，如果引入卷积层，需要一个类似张量的类。
2. 没有引入计算图和自动梯度的概念
3. 没有存储和载入网络的接口，每次都要训练了才能跑测试。
4. 还需要日志接口输出日志信息，测试时需要把分错的样例输出。