如下图所示为阵列探测示意图,其中目标到达角定义为信号入射方向与阵列法线之间的夹角,在窄带(点信源)和远场(平面波)的假设下,同一信号到达不同阵元存在波程差,这个波程差导致了各接收阵元的相位差,该相位差组成阵列的导向矢量和阵列流型矩阵。
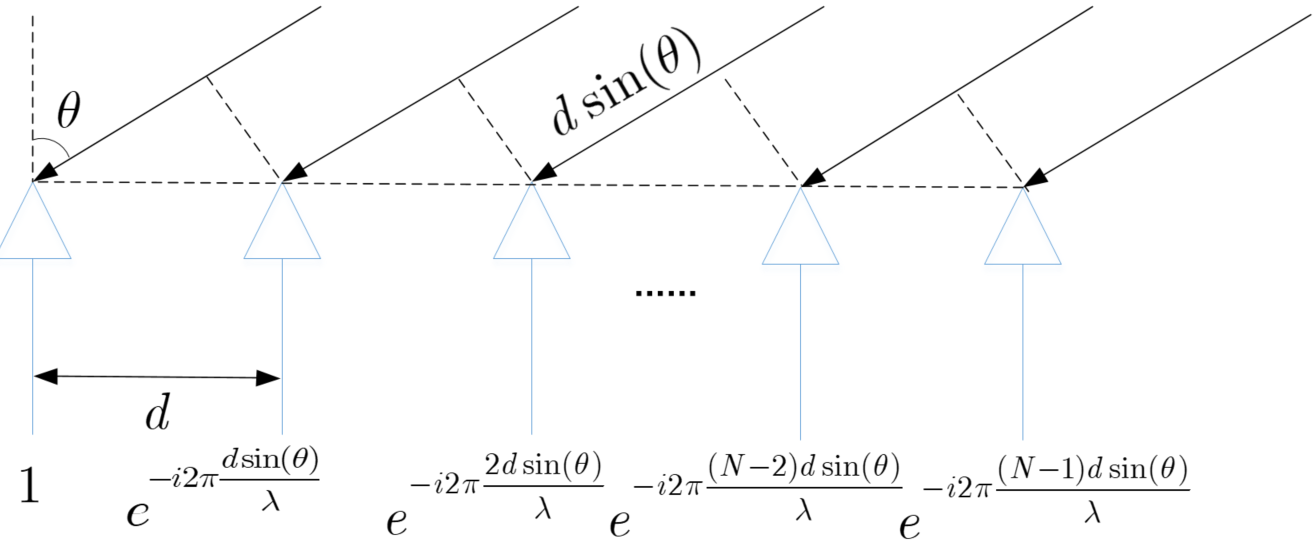
设阵元数为 M M M,信源数为 N N N,第n个信源的到达角为 θ n \theta_n θn则其对应的导向矢量可以表示为 a ( θ n ) = [ 1 , e − i 2 π d s i n ( θ n ) / λ , . . . , e − i 2 π ( M − 1 ) d s i n ( θ N ) / λ ] T \boldsymbol{a}(\theta_n)=[1,e^{-i2\pi d{\rm sin}(\theta_n)/\lambda},...,e^{-i2\pi (M-1)d{\rm sin}(\theta_N)/\lambda}]^T a(θn)=[1,e−i2πdsin(θn)/λ,...,e−i2π(M−1)dsin(θN)/λ]T,所有信源组成的阵列流型矩阵可以表示为
A ( θ ) = [ a ( θ 0 ) , . . . , a ( θ p ) , . . . , a ( θ N − 1 ) ] = [ 1 , 1 , . . . , 1 e − i 2 π d s i n ( θ 0 ) / λ , e − i 2 π d s i n ( θ 1 ) / λ , . . . , e − i 2 π d s i n ( θ N − 1 ) / λ ⋮ , ⋮ , ⋮ , ⋮ e − i 2 π ( M − 1 ) d s i n ( θ 0 ) / λ , e − i 2 π ( M − 1 ) d s i n ( θ 1 ) / λ , . . . , e − i 2 π ( M − 1 ) d s i n ( θ N − 1 ) / λ ] (1) \begin{equation} \begin{aligned} \boldsymbol{A}(\boldsymbol{\theta})&=[\boldsymbol{a}(\theta_0),...,\boldsymbol{a}(\theta_p),...,\boldsymbol{a}(\theta_{N-1})]\\ &= \begin{bmatrix} &1,&1,&...,&1\\ &e^{-i2\pi d{\rm sin}(\theta_0)/\lambda},&e^{-i2\pi d{\rm sin}(\theta_1)/\lambda},&...,&e^{-i2\pi d{\rm sin}(\theta_{N-1})/\lambda}\\ &\vdots,&\vdots,&\vdots,&\vdots\\ &e^{-i2\pi (M-1)d{\rm sin}(\theta_0)/\lambda},&e^{-i2\pi (M-1)d{\rm sin}(\theta_1)/\lambda},&...,&e^{-i2\pi (M-1)d{\rm sin}(\theta_{N-1})/\lambda} \end{bmatrix} \end{aligned} \end{equation}\tag{1} A(θ)=[a(θ0),...,a(θp),...,a(θN−1)]= 1,e−i2πdsin(θ0)/λ,⋮,e−i2π(M−1)dsin(θ0)/λ,1,e−i2πdsin(θ1)/λ,⋮,e−i2π(M−1)dsin(θ1)/λ,...,...,⋮,...,1e−i2πdsin(θN−1)/λ⋮e−i2π(M−1)dsin(θN−1)/λ (1)
从(1)可以看出, A ( θ ) \boldsymbol{A}(\boldsymbol{\theta}) A(θ)是一个范德蒙矩阵,且当 M > = N M>=N M>=N,即信源数小于阵列维数时,阵列流型矢量是非奇异的。
所以阵列信号的接收模型可以表示为
x ( t ) = A ( θ ) s ( t ) + n ( t ) (2) \boldsymbol{x}(t)=\boldsymbol{A}(\boldsymbol{\theta})\boldsymbol{s}(t)+\boldsymbol{n}(t)\tag{2} x(t)=A(θ)s(t)+n(t)(2)
其中 s ( t ) = [ s 0 ( t ) , . . . , s N − 1 ( t ) ] T \boldsymbol{s}(t)=[s_0(t),...,s_{N-1}(t)]^T s(t)=[s0(t),...,sN−1(t)]T, n ( t ) = [ n 0 ( t ) , . . . , n M − 1 ( t ) ] T \boldsymbol{n}(t)=[n_0(t),...,n_{M-1}(t)]^T n(t)=[n0(t),...,nM−1(t)]T。计算阵列接收信号的协方差矩阵如下
R x = E [ x ( t ) x H ( t ) ] = A E [ s ( t ) s H ( t ) ] A H + E [ n ( t ) n H ( t ) ] = A R s A H + σ 2 I (3) \begin{equation} \begin{aligned} \boldsymbol{R}_x&={\rm E}[\boldsymbol{x}(t)\boldsymbol{x}^H(t)]=\boldsymbol{A}{\rm E}[\boldsymbol{s}(t)\boldsymbol{s}^H(t)]\boldsymbol{A}^H+{\rm E}[\boldsymbol{n}(t)\boldsymbol{n}^H(t)]=\boldsymbol{A}\boldsymbol{R}_s \boldsymbol{A}^H+\sigma^2 \boldsymbol{I} \end{aligned} \end{equation}\tag{3} Rx=E[x(t)xH(t)]=AE[s(t)sH(t)]AH+E[n(t)nH(t)]=ARsAH+σ2I(3)
对协方差矩阵进行奇异值分解可以得到
R x = A R s A H + σ 2 I = U Σ U H = [ U s , U n ] [ Σ s , O O , Σ n ] [ U s H U n H ] (4) \boldsymbol{R}_x=\boldsymbol{A}\boldsymbol{R}_s \boldsymbol{A}^H+\sigma^2 \boldsymbol{I}=\boldsymbol{U}\boldsymbol{\Sigma}\boldsymbol{U}^H=[\boldsymbol{U}_s,\boldsymbol{U}_n]\begin{bmatrix}\boldsymbol{\Sigma}_s,\boldsymbol{O}\\ \boldsymbol{O},\boldsymbol{\Sigma}_n\end{bmatrix} \begin{bmatrix}\boldsymbol{U}_s^H\\\boldsymbol{U}_n^H\end{bmatrix}\tag{4} Rx=ARsAH+σ2I=UΣUH=[Us,Un][Σs,OO,Σn][UsHUnH](4)
其中 Σ s = d i a g ( σ 1 2 + σ 2 , . . . , σ N 2 + σ 2 ) = d i a g ( λ 1 , . . . , λ N ) \boldsymbol{\Sigma}_s={\rm diag}(\sigma_1^2+\sigma^2,...,\sigma_{N}^2+\sigma^2)={\rm diag}(\lambda_1,...,\lambda_N) Σs=diag(σ12+σ2,...,σN2+σ2)=diag(λ1,...,λN), Σ n = σ 2 I \boldsymbol{\Sigma}_n=\sigma^2 \boldsymbol{I} Σn=σ2I,令 U = [ u 1 , . . . , u N , ∣ u N + 1 , . . . , u M ] \boldsymbol{U}=[\boldsymbol{u}_1,...,\boldsymbol{u}_N, |\boldsymbol{u}_{N+1},...,\boldsymbol{u}_M] U=[u1,...,uN,∣uN+1,...,uM],则 U s = [ u 1 , . . . , u N ] \boldsymbol{U}_s=[\boldsymbol{u}_1,...,\boldsymbol{u}_N] Us=[u1,...,uN], U n = [ u N + 1 , . . . , u M ] \boldsymbol{U}_n=[\boldsymbol{u}_{N+1},...,\boldsymbol{u}_M] Un=[uN+1,...,uM]。根据奇异值分解的性质可知, U \boldsymbol{U} U是一个酉矩阵, { u 1 , . . . , u M } \lbrace\boldsymbol{u}_1,...,\boldsymbol{u}_M\rbrace {u1,...,uM}构成了一组标准正交基,即 u i H u i = 1 \boldsymbol{u}_i^H\boldsymbol{u}_i=1 uiHui=1, u i H u j = 0 , i ≠ j \boldsymbol{u}_i^H\boldsymbol{u}_j=0,i\neq j uiHuj=0,i=j,基于此,下面来证明一些结果:
(1) U s H U s = I , U n H U n = I \boldsymbol{U}_s^H \boldsymbol{U}_s=\boldsymbol{I},\boldsymbol{U}_n^H \boldsymbol{U}_n=\boldsymbol{I} UsHUs=I,UnHUn=I
证明:
U
s
H
U
s
=
[
u
1
H
⋮
u
N
H
]
[
u
1
,
.
.
.
,
u
N
]
=
[
u
1
H
u
1
,
.
.
.
,
u
1
H
u
N
⋮
,
.
.
.
,
⋮
u
N
H
u
1
,
.
.
.
,
u
N
H
u
N
]
=
I
U
n
H
U
n
=
[
u
N
+
1
H
⋮
u
M
H
]
[
u
N
+
1
,
.
.
.
,
u
M
]
=
[
u
N
+
1
H
u
N
+
1
,
.
.
.
,
u
N
+
1
H
u
M
⋮
,
.
.
.
,
⋮
u
M
H
u
N
+
1
,
.
.
.
,
u
M
H
u
M
]
=
I
\begin{equation} \begin{aligned} \boldsymbol{U}_s^H \boldsymbol{U}_s&=\begin{bmatrix}\boldsymbol{u}_1^H\\ \vdots\\ \boldsymbol{u}_N^H\end{bmatrix} [\boldsymbol{u}_1,...,\boldsymbol{u}_N]=\begin{bmatrix}&\boldsymbol{u}_1^H \boldsymbol{u}_1,&...,&\boldsymbol{u}_1^H \boldsymbol{u}_N \\ &\vdots,&...,&\vdots\\ &\boldsymbol{u}_N^H \boldsymbol{u}_1,&...,&\boldsymbol{u}_N^H \boldsymbol{u}_N\end{bmatrix}=\boldsymbol{I}\\ \boldsymbol{U}_n^H \boldsymbol{U}_n&=\begin{bmatrix}\boldsymbol{u}_{N+1}^H\\ \vdots\\ \boldsymbol{u}_M^H\end{bmatrix} [\boldsymbol{u}_{N+1},...,\boldsymbol{u}_M]=\begin{bmatrix}&\boldsymbol{u}_{N+1}^H \boldsymbol{u}_{N+1},&...,&\boldsymbol{u}_{N+1}^H \boldsymbol{u}_M \\ &\vdots,&...,&\vdots\\ &\boldsymbol{u}_M^H \boldsymbol{u}_{N+1},&...,&\boldsymbol{u}_M^H \boldsymbol{u}_M\end{bmatrix}=\boldsymbol{I}\\ \end{aligned} \end{equation}
UsHUsUnHUn=
u1H⋮uNH
[u1,...,uN]=
u1Hu1,⋮,uNHu1,...,...,...,u1HuN⋮uNHuN
=I=
uN+1H⋮uMH
[uN+1,...,uM]=
uN+1HuN+1,⋮,uMHuN+1,...,...,...,uN+1HuM⋮uMHuM
=I
(2)
U
s
U
s
H
+
U
n
U
n
H
=
I
\boldsymbol{U}_s \boldsymbol{U}_s^H+\boldsymbol{U}_n \boldsymbol{U}_n^H=\boldsymbol{I}
UsUsH+UnUnH=I
证明:
U
s
U
s
H
=
[
u
1
,
.
.
.
,
u
N
]
[
u
1
H
⋮
u
N
H
]
=
∑
i
=
1
N
u
i
u
i
H
U
n
U
n
H
=
[
u
N
+
1
,
.
.
.
,
u
M
]
[
u
N
+
1
H
⋮
u
M
H
]
=
∑
i
=
N
+
1
M
u
i
u
i
H
U
s
U
s
H
+
U
n
U
n
H
=
∑
i
=
1
M
u
i
u
i
H
\begin{equation} \begin{aligned} \boldsymbol{U}_s \boldsymbol{U}_s^H&=[\boldsymbol{u}_1,...,\boldsymbol{u}_N]\begin{bmatrix}\boldsymbol{u}_1^H\\ \vdots\\ \boldsymbol{u}_N^H\end{bmatrix}=\sum_{i=1}^N \boldsymbol{u}_i \boldsymbol{u}_i^H\\ \boldsymbol{U}_n \boldsymbol{U}_n^H&=[\boldsymbol{u}_{N+1},...,\boldsymbol{u}_M]\begin{bmatrix}\boldsymbol{u}_{N+1}^H\\ \vdots\\ \boldsymbol{u}_M^H\end{bmatrix}=\sum_{i=N+1}^M \boldsymbol{u}_i \boldsymbol{u}_i^H\\ &\boldsymbol{U}_s \boldsymbol{U}_s^H+\boldsymbol{U}_n \boldsymbol{U}_n^H=\sum_{i=1}^M \boldsymbol{u}_i \boldsymbol{u}_i^H \end{aligned} \end{equation}
UsUsHUnUnH=[u1,...,uN]
u1H⋮uNH
=i=1∑NuiuiH=[uN+1,...,uM]
uN+1H⋮uMH
=i=N+1∑MuiuiHUsUsH+UnUnH=i=1∑MuiuiH
而
u
i
u
i
H
=
C
,
C
i
,
j
=
{
0
,
i
≠
j
1
,
i
=
j
\boldsymbol{u}_i \boldsymbol{u}_i^H=\boldsymbol{C},C_{i,j}=\begin{cases}0,i\neq j\\ 1,i=j\end{cases}
uiuiH=C,Ci,j={0,i=j1,i=j,所以,显然有
U
s
U
s
H
+
U
n
U
n
H
=
I
\boldsymbol{U}_s \boldsymbol{U}_s^H+\boldsymbol{U}_n \boldsymbol{U}_n^H=\boldsymbol{I}
UsUsH+UnUnH=I
(3) U s U s H = U s ( U s H U s ) − 1 U s H \boldsymbol{U}_s \boldsymbol{U}_s^H=\boldsymbol{U}_s (\boldsymbol{U}_s^H \boldsymbol{U}_s)^{-1}\boldsymbol{U}_s^H UsUsH=Us(UsHUs)−1UsH, U n U n H = U n ( U n H U n ) − 1 U n H = I − U s ( U s H U s ) − 1 U s H \boldsymbol{U}_n \boldsymbol{U}_n^H=\boldsymbol{U}_n (\boldsymbol{U}_n^H \boldsymbol{U}_n)^{-1}\boldsymbol{U}_n^H=\boldsymbol{I}-\boldsymbol{U}_s (\boldsymbol{U}_s^H \boldsymbol{U}_s)^{-1}\boldsymbol{U}_s^H UnUnH=Un(UnHUn)−1UnH=I−Us(UsHUs)−1UsH
证明:由证明1可得 U s H U s = I , U n H U n = I \boldsymbol{U}_s^H \boldsymbol{U}_s=\boldsymbol{I},\boldsymbol{U}_n^H \boldsymbol{U}_n=\boldsymbol{I} UsHUs=I,UnHUn=I,所以 U s U s H = U s ( U s H U s ) − 1 U s H \boldsymbol{U}_s \boldsymbol{U}_s^H=\boldsymbol{U}_s (\boldsymbol{U}_s^H \boldsymbol{U}_s)^{-1}\boldsymbol{U}_s^H UsUsH=Us(UsHUs)−1UsH和 U n U n H = U n ( U n H U n ) − 1 U n H \boldsymbol{U}_n \boldsymbol{U}_n^H=\boldsymbol{U}_n (\boldsymbol{U}_n^H \boldsymbol{U}_n)^{-1}\boldsymbol{U}_n^H UnUnH=Un(UnHUn)−1UnH显然是成立的,再由证明结果2,可以得到 U n U n H = U n ( U n H U n ) − 1 U n H = I − U s ( U s H U s ) − 1 U s H \boldsymbol{U}_n \boldsymbol{U}_n^H=\boldsymbol{U}_n (\boldsymbol{U}_n^H \boldsymbol{U}_n)^{-1}\boldsymbol{U}_n^H=\boldsymbol{I}-\boldsymbol{U}_s (\boldsymbol{U}_s^H \boldsymbol{U}_s)^{-1}\boldsymbol{U}_s^H UnUnH=Un(UnHUn)−1UnH=I−Us(UsHUs)−1UsH也是成立的。
由上面的证明结果(3)可知, U s U s H \boldsymbol{U}_s \boldsymbol{U}_s^H UsUsH和 U n U n H \boldsymbol{U}_n \boldsymbol{U}_n^H UnUnH分别表示在s空间和n空间上的投影算子,所以 U s U s H X \boldsymbol{U}_s \boldsymbol{U}_s^H X UsUsHX, U n U n H X \boldsymbol{U}_n\boldsymbol{U}_n^H X UnUnHX分别表示将信号 X \boldsymbol{X} X往s空间和n空间上进行投影,基于这个性质可以做很多事情。
(4)可以写成
R
x
=
[
U
s
,
U
n
]
[
Σ
s
,
O
O
,
Σ
n
]
[
U
s
H
U
n
H
]
=
U
s
Σ
s
U
s
H
+
U
n
Σ
n
U
n
H
=
∑
i
=
1
N
λ
i
u
i
u
i
H
+
∑
i
=
N
+
1
M
σ
2
u
i
u
i
H
(5)
\boldsymbol{R}_x=[\boldsymbol{U}_s,\boldsymbol{U}_n]\begin{bmatrix}\boldsymbol{\Sigma}_s,\boldsymbol{O}\\ \boldsymbol{O},\boldsymbol{\Sigma}_n\end{bmatrix} \begin{bmatrix}\boldsymbol{U}_s^H\\\boldsymbol{U}_n^H\end{bmatrix}=\boldsymbol{U}_s\boldsymbol{\Sigma}_s\boldsymbol{U}_s^H+\boldsymbol{U}_n\boldsymbol{\Sigma}_n\boldsymbol{U}_n^H=\sum_{i=1}^N \lambda_i \boldsymbol{u}_i \boldsymbol{u}_i^H+\sum_{i=N+1}^M \sigma^2 \boldsymbol{u}_i \boldsymbol{u}_i^H\tag{5}
Rx=[Us,Un][Σs,OO,Σn][UsHUnH]=UsΣsUsH+UnΣnUnH=i=1∑NλiuiuiH+i=N+1∑Mσ2uiuiH(5)
对
R
x
\boldsymbol{R}_x
Rx求逆可以得到
R
x
−
1
=
∑
i
=
1
N
1
λ
1
u
i
u
i
H
+
∑
i
=
N
+
1
M
1
σ
2
u
i
u
i
H
(6)
\boldsymbol{R}_x^{-1}=\sum_{i=1}^N \frac{1}{\lambda_1} \boldsymbol{u}_i \boldsymbol{u}_i^H+\sum_{i=N+1}^M \frac{1}{\sigma^2} \boldsymbol{u}_i \boldsymbol{u}_i^H\tag{6}
Rx−1=i=1∑Nλ11uiuiH+i=N+1∑Mσ21uiuiH(6)
现在考虑杂波抑制前的场景,此时信号中的直达波和多径杂波信号远远强于目标信号和噪声信号,所以上述s空间即为杂波空间,n空间即为目标和噪声空间。由于
λ
1
,
.
.
.
,
λ
N
≫
σ
2
\lambda_1,...,\lambda_N \gg \sigma^2
λ1,...,λN≫σ2,所以可以对(6)进行如下近似
R
x
−
1
≈
∑
i
=
N
+
1
M
1
σ
2
u
i
u
i
H
=
1
σ
2
U
n
U
n
H
(7)
\boldsymbol{R}_x^{-1}\approx \sum_{i=N+1}^M \frac{1}{\sigma^2} \boldsymbol{u}_i\boldsymbol{u}_i^H=\frac{1}{\sigma^2}\boldsymbol{U}_n\boldsymbol{U}_n^H\tag{7}
Rx−1≈i=N+1∑Mσ21uiuiH=σ21UnUnH(7)
结合上面证明(3)的结论可知,此时
R
x
−
1
\boldsymbol{R}_x^{-1}
Rx−1等效于n空间的投影算子。所以利用
R
x
−
1
\boldsymbol{R}_x^{-1}
Rx−1可以将原始信号往能量较弱的信号成分构成的子空间进行投影,可以较好地实现信号分离,正是有这样的性质,在很多空域处理算法中经常能看到
R
x
−
1
\boldsymbol{R}_x^{-1}
Rx−1的身影。所以
R
x
\boldsymbol{R}_x
Rx在空域信号处理中具有举足轻重的地位。
[1]H. Krim and M. Viberg, “Two decades of array signal processing research: the parametric approach,” IEEE Signal Process. Mag., vol. 13, no. 4, pp. 67–94, 1996.
[2]Wan X, Yi J, Zhao Z, et al. Experimental research for CMMB-based passive radar under a multipath environment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(1): 70-85.






















 3406
3406











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








