PCA算法主要用于提取对象的主成分及降维,它和奇异值分解(SVD)方法有很紧密的联系,或者说在降维方面是SVD的一种包装和体现。
特征值分解:矩阵A的特征定义为Avi=λivi,vi为特征值λi对应的特征向量。
A可以分解为其中P是由A的特征向量组成的正交阵,∧是由A的特征值组成对角线的对角阵。其相应位置是一一对应的。
例如
P=[v1,v2,v3],

矩阵的物理意义是线性变换,将矩阵做特征值分解后,线性变换可以理解成:在特征向量方向做对应特征值大小的缩放变换。最大特征值对应的特征向量方向,可以理解为该矩阵变换的最主要的方向。如果矩阵的维数很高,但它具有较多很小的特征值,那在变换时可以忽略这些特征值(以及对应特征向量),将线性变换转变成A’=P’∧P’-1,也是一种进行线性变换的近似。
Matlab指令[v d]=eig(A)
奇异值分解:我理解的奇异值分解是从特征值分解衍生出来的。只有方阵才能进行特征值分解,但任何矩阵都可以进行奇异值分解,它的第一步是A·At或At·A或得一个方阵,再进行特征值分解。
奇异值分解的定义为:任一m*n矩阵,总存能分解成m*m的正交矩阵U,m*n阵S,及m*m的正交阵V的转置相乘。
Umm是将Amn*AmnT特征值分解得到的特征向量组成的正交阵,Vmm是将AmnT*Amn做特征值分解得到的特征向量组成的正交阵。Smn是Amn*AmnT的特征值的开方(半正定对角矩阵),是矩阵Umm对应的特征值矩阵。
奇异值分解的物理意义:还是将Amn看做一个线性变换,不过是从n维映射到m维的线性变换。这一变换可以看成从原始域的一个正交方向V,至变换域另一个正交方向U,每个方向有一个缩放程度,缩放程度由Smn来表征。
采用SVD降维的思想是,并非映射到n维,而是映射到r维(r<n),奇异值按从大到小排列,选择前r个,(Amn*AmnT的奇异值共有n个),通常前几个特征值就占所有特征值的90%以上,那么这是进行降维很好的场合。
Matlab指令[u s v]=svd(A);
http://www.ams.org/samplings/feature-column/fcarc-svd在二维下直观详细解释了SVD的 几何意义,以及采用SVD进行降维的几个例子。
Pca和svd什么关系?
1.pca在变换时,最后的结果相当于AP=A’,P为变换矩阵。
我们给svd的式子左右两边乘以V,可以得到
而pca可以写作:
上一篇里对raw face处理的过程中的矩阵变换式为:
可以看到这也可以理解为采用svd进行处理的过程。原始几何为Am3,P33是Am3T*Am3的正交特征向量组,也就是V33。Am3T*Am3/(m-1)就是协方差矩阵,它分解出的正交特征向量与An3T*An3分解的是相同的。
2.pca变换常用于降维和压缩,但一次只能压缩行或者列,看你是用AT·A还是A·AT做特征值分解。而用svd进行压缩,既可以看成是对行的压缩,也可以看成对列压缩。(这里是参照这篇文章的介绍http://www.myhack58.com/Article/sort099/sort0100/2014/51017_3.htm)我还是觉得,如果要在另一个方向压缩,应该是要用
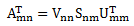
3.采用svd进行压缩的特点是,将矩阵分为三个小矩阵进行储存。在对奇异值进行舍弃后,其储存矩阵所需要的元素也小了,完成压缩。








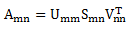
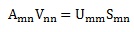
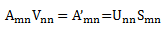
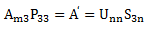














 944
944

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








