分治 —— 莫队算法 —— 带修莫队

【概述】

普通莫队由于强制离线是不能修改的，但对于强制在线的题，可以在普通莫队的基础上强行加上一维时间轴 time，表示这次操作的时间，即在每个询问前已经完成了多少次修改。

简单来说，就是将询问 [l,r]，变为 [l,r,time]，那么指针也可在时间维度上移动，使得第一关键字是左端点所在的块，第二关键字是右端点所在的块，第三关键字是时间，即 [l,r,time] 多了一维可移动的方向：

• [l-1,r,time]
• [l+1,r,time]
• [l,r-1,time]
• [l,r+1,time]
• [l,r,time-1]
• [l,r,time+1]

int l=1,r=0,time=0;
for(int i=1;i<=m;++i){
    int ql=q[i].l,qr=q[i].r;//询问的左右端点
    int qtime=q[i].time;//询问的时间轴
    while(l>ql) add(--l);//[l-1,r,time]
    while(l<ql) del(l++);//[l+1,r,time]
    while(r<qr) add(++r);//[l,r+1,time]
    while(r>qr) del(r--);//[l,r-1,time]
    while(time<qtime) change(i,++time);//[l,r,time+1]
    while(time>qtime) change(i,time--);//[l,r,time-1]
    res[q[i].id]=ans;//获取答案
}

暴力查询时，如果当前修改数比询问的修改数少就把没修改的进行修改，反之回退，需要注意的是，修改分为两部分：

• 若修改的位置在当前区间：更新答案
• 无论修改的位置是否在当前区间：都要进行修改，以供 add 和 del 函数在以后更新答案

struct Change{
    int pos;//要修改的位置
    int col;//要改成的值
}c[N];
void add(int x){...}//统计新的，根据具体情况修改
void del(int x){...}//减去旧的，根据具体情况修改
void change(int x,int ti){//改变时间轴
    if(c[ti].pos>=q[x].l&&c[ti].pos<=q[x].r){
        del(a[c[ti].pos]);//删除指定位置上的值
        add(c[ti].col);//统计新的数
    }
    swap(c[ti].col,a[c[ti].pos]);//直接互换，下次执行时必定是回退这次操作
}
/*
    change函数会执行或回退修改ti,
    执行还是回退取决于是否执行过，
    x表明当前的询问是x，
    即若修改了区间[q[x].l,q[x].r],
    便要更新答案
*/

【排序】

由于第一关键字是左端点所在的块，第二关键字是右端点所在的块，第三关键字是时间，虽然多了一个维度，但转移仍是 O(1) 的复杂度，只需要在排序时考虑 time 的影响即可。

• 当左右端点在同一个块中：以 time 为关键字排序
• 当左端点在同一个块中，右端点不在：以右端点为关键字排序
• 当左端点不在同一个块：以左端点为关键字排序

bool cmp(Node a,Node b){//排序
    if( (a.l/block)==(b.l/block) ){//当左端点位于同一个块时
        if( (a.r/block)==(b.r/block) )//当右端点位于同一个块时
            return a.time<b.time;
        else
            return a.r<b.r;
    }
    else//当左端点不位于同一个块时
        return a.l<b.l;
    //return (a.l/block)^(b.l/block) ? a.l<b.l : ( ((a.r/block)^(b.r/block))?a.r<b.r:a.time<b.time );
}

【分块与时间复杂度】

设 block 为分块大小，c 为修改个数，q 为询问个数，l、r 块表示以 l/block、r/block 分的块，每个 l 块包含 n/block 个 r 块

• 对于时间指针 time，每个 r 块最多会移动 c 次，共有  个 r 块，总移动次数为 
• 对于左端点指针 l：l 块内最多移动 block 次，换 l 块时最多移动 2*block 次，总移动次数为：
• 对于右端点指针 r：总移动次数为：
  • r 块内最多移动 block 次，换 r 块时最多移动 2*block 次，所有 l 块内移动次数之和为 
  • 换 l 块时最多移动 n 次，总的换 l 块时移动次数之和为 

故总移动次数为：，因而总时间复杂度为 

由于一般题目不会分别告诉修改与询问的个数，统一用 m 表示，则有：

通过 Mathermatica 软件分析，要想让总时间复杂度最小，可以得到 block 的取值如下：

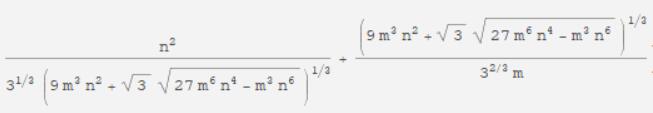
由于式子过于复杂，难以写出带修莫队的最佳分块数，因此一般视作 n=m，即有：

令总时间复杂度最小，可得到当  时最小，此时总时间复杂度为：

综上，分块一般以  为一块，分成  个块，总时间复杂度为：

int block=pow(n,0.66666);

 【模版】

struct Node{
    int l,r;//询问的左右端点
    int time;//时间维度
    int id;//询问的编号
}q[N];
struct Change{
    int pos;//要修改的位置
    int col;//要改成的值
}c[N];
int n,m,a[N];
int block;//分块
int numQ,numC;//查询、修改操作的次数
LL ans,cnt[N];
LL res[N];

bool cmp(Node a,Node b){//排序
    return (a.l/block)^(b.l/block) ? a.l<b.l : ((a.r/block)^(b.r/block)?a.r<b.r:a.time<b.time);
}

void add(int x){//统计新的，根据具体情况修改
    if(cnt[x]==0)
        ans++;
    cnt[x]++;

}
void del(int x){//减去旧的，根据具体情况修改
    cnt[x]--;
    if(cnt[x]==0)
        ans--;
}
void change(int x,int ti){//改变时间轴
    if(c[ti].pos>=q[x].l&&c[ti].pos<=q[x].r){
        del(a[c[ti].pos]);//删除指定位置上的值
        add(c[ti].col);//统计新的数
    }
    swap(c[ti].col,a[c[ti].pos]);//直接互换，下次执行时必定是回退这次操作
}
int main(){
    while(scanf("%d%d",&n,&m)!=EOF){
        ans=0;
        numQ=0;
        numC=0;
        memset(cnt,0,sizeof(cnt));
        block=pow(n,0.66666);//分块

        for(int i=1;i<=n;i++)
            scanf("%d",&a[i]);

        for(int i=1;i<=m;i++){
            char op[10];
            scanf("%s",op);
            if(op[0]=='Q'){//查询操作
                ++numQ;//查询操作次数+1
                scanf("%d%d",&q[numQ].l,&q[numQ].r);
                q[numQ].id=numQ;//序号
                q[numQ].time=numC;//时间轴
            }
            else{//修改操作
                ++numC;//修改操作次数+1
                scanf("%d%d",&c[numC].pos,&c[numC].col);
            }
        }
        sort(q+1,q+numQ+1,cmp);//对询问进行排序
        int l=1,r=0,time=0;//左右指针与时间轴
        for(int i=1;i<=numQ;i++){
            int ql=q[i].l,qr=q[i].r;//询问的左右端点
            int qtime=q[i].time;//询问的时间轴
            while(l>ql) add(a[--l]);//[l-1,r,time]
            while(l<ql) del(a[l++]);//[l+1,r,time]
            while(r<qr) add(a[++r]);//[l,r+1,time]
            while(r>qr) del(a[r--]);//[l,r-1,time]
            while(time<qtime) change(i,++time);//[l,r,time+1]
            while(time>qtime) change(i,time--);//[l,r,time-1]
            res[q[i].id]=ans;//获取答案
        }

        for(int i=1;i<=numQ;i++)
            printf("%lld\n",res[i]);
    }
    return 0;
}