Graph Coloring（POJ-1419）_grapf coloring问题-CSDN博客

本文链接：https://blog.csdn.net/u011815404/article/details/88408783

本文探讨了一种针对特定图的最优染色算法，旨在找到图中可染为黑色的最大节点集合，确保任意两个相邻节点不同时为黑色。通过转换为求解最大独立集问题，并利用Bron-Kerbosch算法在补图上寻找最大团，实现了解决方案。文章提供了详细的源代码及样例输入输出，便于理解与实践。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Problem Description

You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black.

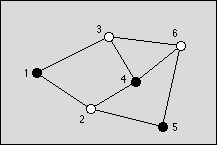
Figure 1: An optimal graph with three black nodes

Input

The graph is given as a set of nodes denoted by numbers 1...n, n <= 100, and a set of undirected edges denoted by pairs of node numbers (n1, n2), n1 != n2. The input file contains m graphs. The number m is given on the first line. The first line of each graph contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.

Output

The output should consists of 2m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is given by the list of black nodes, separated by a blank.

Sample Input

1
6 8
1 2
1 3
2 4
2 5
3 4
3 6
4 6
5 6

Sample Output

3
1 4 5

题意：n 个点 m 条边，点的序号从 1 到 n，边为无向边，现在给图中的点染色，只能染黑色或者白色，且要求相邻结点不能同时为黑色，问图中染黑色的结点的最大个数以及结点位置

思路：

由于要求相邻结点不能同时为黑色，那么黑色就变成了一个独立集，那么实质就是要计算图中的最大独立子集

由于最大独立集=补图最大团，那么直接采用 Bron-Kerbosch 算法建立反图计算最大团即可

Source Program

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define PI acos(-1.0)
#define E 1e-9
#define INF 0x3f3f3f3f
#define LL long long
const int MOD=1E9+7;
const int N=1000+5;
const int dx[]= {-1,1,0,0};
const int dy[]= {0,0,-1,1};
using namespace std;

int n,m;
bool G[N][N];
int cnt[N];//cnt[i]为>=i的最大团点数
int group[N];//最大团的点
int vis[N];//记录点的位置
int res;//最大团的数目
bool dfs(int pos,int num){//num为当前独立集中的点数
    for(int i=pos+1;i<=n;i++){
        if(cnt[i]+num<=res)//剪枝，若取i但cnt[i]+已经取了的点数仍<ans
            return false;

        if(G[pos][i]){//与当前团中元素比较，取Non-N(i)
            int j;
            for(j=0;j<num;j++)
                if(!G[i][vis[j]])
                    break;
            if(j==num){//若为空，则皆与i相邻，则此时将i加入到最大团中
                vis[num]=i;
                if(dfs(i,num+1))
                    return true;
            }
        }
    }

    if(num>res){//每添加一个点最多使最大团数+1,后面的搜索就没有意义了
        for(int i=0;i<num;i++)//最大团的元素
            group[i]=vis[i];
        res=num;//最大团中点的数目
        return true;
    }
    return false;
}
void maxClique(){
    res=-1;
    for(int i=n;i>0;i--){//枚举所有点
        vis[0]=i;
        dfs(i,1);
        cnt[i]=res;
    }
}
int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        memset(G,0,sizeof(G));

        scanf("%d%d",&n,&m);
        for(int i=0;i<m;i++){
            int x,y;
            scanf("%d%d",&x,&y);
            G[x][y]=1;
            G[y][x]=1;
        }

        //建立反图
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(i==j)
                    G[i][j]=0;
                else
                    G[i][j]^=1;
            }
        }
        maxClique();

        if(res<0)
            res=0;
        printf("%d\n",res);//最大团的个数
        for(int i=0;i<res;i++)//最大团中的顶点
            printf("%d ",group[i]);
        printf("\n");
    }
    return 0;
}