【概述】
组合数取模,即计算组合数 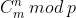 ,由于
,由于  ,同余定理对除法不适用,因此需要使用别的方法来解决这个问题
,同余定理对除法不适用,因此需要使用别的方法来解决这个问题
常见的方法有:使用逆元对组合数取模、递推打表取模、卢卡斯定理、扩展卢卡斯定理等,这些方法应用的场景各不相同。
- 使用逆元:要求 p 是质数,时间复杂度 O(n)
- 递推打表:要求 n、m 不大于 10000,时间复杂度 O(n^2)
- 卢卡斯定理:要求 p 是质数,且 m、n 很大但 p 很小 或者 n、m 不大但大于 p
- 扩展卢卡斯定理:要求 p 不是质数,且 m、n 很大但 p 很小 或者 n、m 不大但大于 p
【方法】
【例题】
- Xiao Ming's Hope(HDU-4349)(公式推导):点击这里
- 机器人走方格(51Nod-1119)(卢卡斯定理):点击这里
- Combinations(LightOJ-1067)(卢卡斯定理):点击这里
- Problem Makes Problem(LightOJ-1102)(卢卡斯定理):点击这里
- Applese 的大奖(2019牛客寒假算法基础集训营 Day4-I)(逆元求组合数):点击这里
- いろはちゃんとマス目 / Iroha and a Grid(AtCoder-1974)(逆元求组合数):点击这里
- 11(AtCoder-2649)(容斥原理+递推求逆元):点击这里
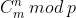 ,由于
,由于  ,同余定理对除法不适用,因此需要使用别的方法来解决这个问题
,同余定理对除法不适用,因此需要使用别的方法来解决这个问题

























 822
822

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








