智能优化算法：黄金正弦算法 -附代码

智能优化算法：黄金正弦算法

摘要：黄金正弦算法(Gold-SA)是 Tanyildizi 等 于2017 年提出的一种新型元启发式优化算法，其灵感来源于正弦函数单位圆内扫描类似于待优化问题解的空间搜索，并通过黄金分割率缩小搜索空间以逼近算法最优解。与传统元启发式优化算法相比，Gold-SA 算法具有原理简单、设置参数少、寻优能力强等特点。

1.算法原理

1.1 初始化

与其他基于种群的优化算法一样，Gold-SA 算法也从随机生成的种群开始。Gold-SA 算法初始种群旨在通过随机生成每个维度的均匀分布来更好地扫描搜索空间。
$$V_i=rand\ast (ub-lb)+lb\text{\hspace{1em}(1)}$$
式中 $V_i$ 第$i$个个体初始值;$ub,lb$为搜索空间上下限值。

1.2 黄金分割系数

Gold-SA 算法在位置更新过程中引入黄金分割系数 $x_1,x_2$ 使“搜索”和“开发”达到良好的平衡，这些系数缩小了搜索空间引
领个体趋近最优值。$x_1,x_2$ 表示如式(2)、(3):
$$x_1=a\ast (1-t)+b\ast t\text{\hspace{1em}(2)}$$

$$x_2=a\ast t+b\ast (1-t)\text{\hspace{1em}(3)}$$

式中 $a、b$为黄金分割比率搜索初始值,一般$a=-\pi ,b=\pi$,t为黄金分比率。$t=(\sqrt{5}-1)/2$

1.3 位置更新

随着迭代次数的增加，Gold-SA算法通过式(4)进行位置更新
$$V_i^{t+1}=V_i^t|sin(r1)|-r_{2}sin(r_1)|x_1{D}_i^t-x_2{V}_i^t|\text{\hspace{1em}(4)}$$
式中$V_i^{t+1}$第 i 个个体第 t + 1 次迭代位置;$V_i^t$第 i 个个体第 t 次迭代位置;$D_i^t$第 i 个个体第 t 次迭代最优位置;$r_1$为$[0,2\pi ]$范围内的随机数；$r_2$为$[0,\pi ]$范围内的随机数；$x_1,x_2$为黄金分割系数。

算法流程如下：

Step1.初始化参数，设置黄金正弦相关参数

Step2.计算适应度值

Step3.计算黄金分割率

Step4.根据位置更新公式，更新位置。

Step5.计算适应度值，并更新最优位置，记录最优位置。

Step6.判断是否达到迭代结束条件，如果达到则输出最后结果，否则重复不揍Step1-6.

2.实验结果

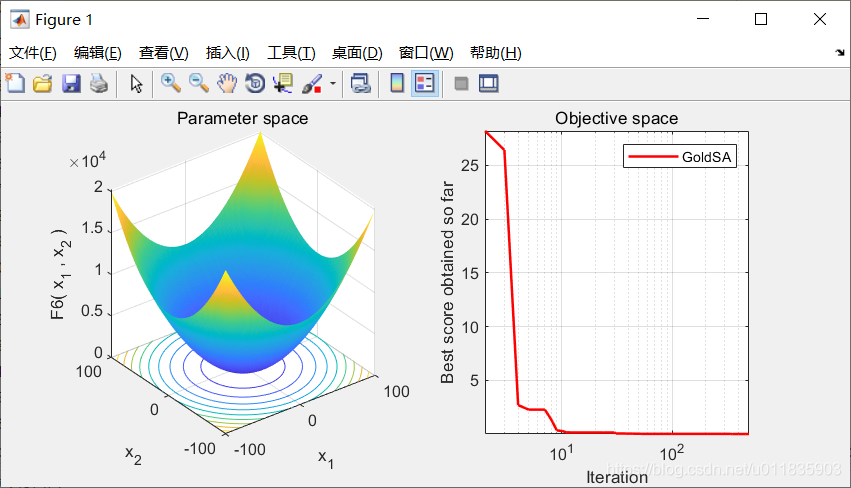
3.参考文献

[1] TANYILDIZI E，DEMIＲ G. Golden sine algorithm: a novel math inspired algorithm［J］. Advances in Electrical and Computer Engineering，2017，17(2): 71 －79.

[2] 周有荣,李娜,周发辉.黄金正弦算法在水文地质参数优化中的应用[J].人民珠江,2020,41(06):117-120+128.

4.Matlab代码

黄金正弦算法
算法相关应用

名称	说明或者参考文献
黄金正弦算法在水文地质参数优化中的应用	[1] 周有荣, 李娜, 周发辉. 黄金正弦算法在水文地质参数优化中的应用[J]. 人民珠江, 2020, 041(006):117-120,128.

5.Python代码

个人资料介绍